相关试卷
-
1、在中, , , , 点为边边上一动点,将沿着翻折,使得点到达 , 且平面平面 , 则当最小时,的长度为.
-
2、如图,在正方体中,异面直线与所成角的大小为.

-
3、如图,在棱长为1的正方体中,是线段上的动点(含端点),则( )
 A、面 B、与是异面直线 C、的最小值为 D、三棱锥的体积为定值
A、面 B、与是异面直线 C、的最小值为 D、三棱锥的体积为定值 -
4、已知向量 , 满足 , , 则( )A、的最大值是3 B、的最小值是0 C、的最大值是 D、的最小值是4
-
5、已知函数 , 下列结论正确的是( )A、函数的最小正周期为 B、函数的图象对于点对称 C、函数在单调递增 D、函数在上的值域是
-
6、在中,角A,B,C的对边分别是a,b,c若 , , , 则下列结论不正确的是( )A、 B、 C、的面积为6 D、
-
7、二次函数的图象与x轴相交于A,B两点,点C在二次函数图象上,且到轴距离为4, , 则a的值为( )A、4 B、2 C、 D、
-
8、在中, , , 则A、 B、 C、 D、
-
9、一个圆台的上、下底面的半径分别为和 , 体积为 , 则它的表面积为( )A、 B、 C、 D、
-
10、在中,角的对边分别是 . 已知 , 则( )A、 B、 C、 D、
-
11、已知 , , 与的夹角为 , 则在方向上的投影向量为( )A、 B、 C、 D、
-
12、锐角三角形中,角的对边分别为且.(1)、求;(2)、求三角形周长的取值范围;(3)、求三角形面积的最大值.
-
13、已知各项均为正整数的数列满足.(1)、若 , 求;(2)、已知.
(i)求;
(ii)证明:可以为定值,且当为定值时,.
-
14、如图,在三棱柱中,为的重心,平面 , 记二面角与的大小分别为.
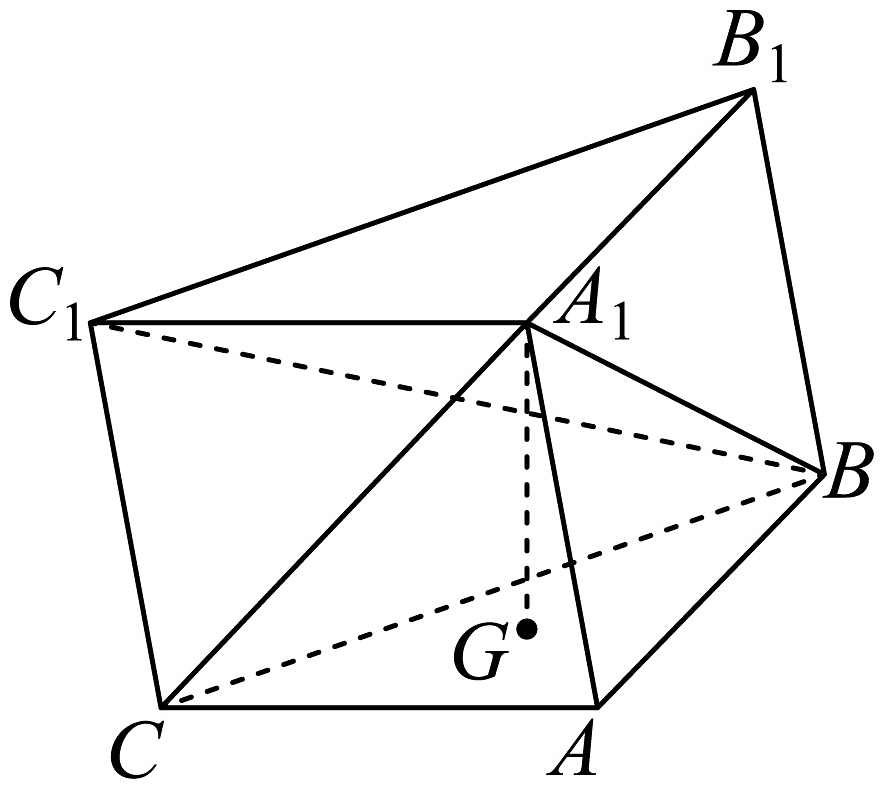 (1)、当时,时.
(1)、当时,时.(i)证明:;
(ii)求;
(2)、若 , 求的取值范围. -
15、已知函数.(1)、若 , 求的最小值;(2)、若函数在上单调递增,求的取值范围.
-
16、已知分别是轴,轴上的动点, , 若点满足 , 记的轨迹为.(1)、求的方程;(2)、是上一点,若 , 求直线的方程.
-
17、某企业前8个月月底的盈利金额(万元)与月份之间的关系如下表所示:
1
2
3
4
5
6
7
8
1.95
2.92
4.38
6.58
9.87
15.00
22.50
33.70
(1)、用模拟与的关系,求出回归方程;(2)、根据(1)的结果计算,在几月份的月底统计的盈利金额开始超过60万元?附:①;
②;
③回归直线中斜率和截距的最小二乘估计公式为:.
-
18、已知分别为双曲线的左、右焦点,在上,其中在第一象限,在第二象限,直线过 , 且关于直线对称,则四边形的面积为.
-
19、从1至8的8个整数中随机取2个不同的数组成一个两位数,则该数能被3整除的概率为.
-
20、记为正项等比数列的公比,若 , 则.