相关试卷
-
1、下列方程中，与2x-40=50 的解不同的是( )。A、2x-40+20=50+20 B、4x-80=100 C、2x=60+30 D、2x-30=40
-
2、在(35-5n)÷4中，当n=时，式子的结果是0；当n=时，式子的结果是5。
-
3、解方程2(x+4)=10时，可以把看作一个整体，方程两边同时除以 ， 把方程变为 x +4=5；也可以利用把方程变为2x+8=10。
-
4、小新与小翼做数学游戏，他们同时从分别写着5、6、7、8的四张卡片中各抽出一张，再把两人抽到的卡片上的数相乘，若积是单数，则小新赢；若积是双数，则小翼赢。(1)、把表格补充完整。
卡片1
卡片2
积
结果
5
6
30
小翼赢
5
7
35
小新赢
5
(2)、你觉得这个游戏公平吗？请说明理由。(3)、请你设计一个公平的游戏规则。 -
5、从
五张卡片中任意选出两张，得到积是( )的可能性最大。 A、2 B、6 C、3 D、0 -
6、师生两人玩掷两枚一元硬币的游戏，规定：两枚硬币落地后朝上的面图案一样算老师赢，图案不一样算学生赢，比较两人赢的可能性，( )。A、老师大 B、学生大 C、一样大 D、无法确定
-
7、同时掷3枚骰子，朝上的点数之和最大是 ， 最小是。
-
8、同时掷两枚骰子，先将朝上的点数之和填入表格中，再回答下列问题。
(1)、朝上的点数之和共有种情况，最小是 ， 最大是。(2)、朝上的点数之和是1 或13。(填“可能”“不可能”或“一定”)(3)、朝上的点数之和是的可能性最大。(4)、将表格中朝上的点数之和出现的次数情况绘制成条形统计图。
(5)、小优和乐乐进行掷骰子比赛，同时掷出两枚骰子，朝上的点数之和为2 ~7，小优获胜；朝上的点数之和为8 ~12，乐乐获胜。获胜的可能性大。 -
9、任意掷一枚骰子，朝上的点数有种可能，掷出每个点数的可能性。
-
10、为了庆祝某商场成立十周年，策划人员计划设计一个抽奖活动。请你根据要求帮策划人员设计一个转盘。
要求：①设立一、二、三等奖。
②当转盘转动100 次后，指针指向三等奖区域大约有50次，指针指向一等奖、二等奖区域大约各有25次。
-
11、按要求制作数字卡片。(卡片上都是一位数)
①不可能出现3、6、9以外的数字。
②可能抽到6。
③抽到3 的可能性最小。
④抽到9 的可能性最大。
-
12、 五⑴班的同学在不透明的黑色袋子里摸大小相同，颜色分别为白、黄、红的乒乓球。每次摸出一个乒乓球，记录颜色后再放回摇匀，一共摸了30 次。摸出各种颜色乒乓球的次数如下表。
记录
次数
白色乒乓球
18
黄色乒乓球
4
红色乒乓球
8
下面说法正确的有( )个。
①再摸一次，最有可能摸出白色乒乓球
②再摸一次，不可能摸出黄色乒乓球
③再摸一次，一定能摸出白色乒乓球
④再摸一次，有可能摸出黄色乒乓球
A、1 B、2 C、3 D、4 -
13、小新做摸球游戏，他任意摸了200 次，摸到红球37 次、蓝球163 次。根据数据推测，他最有可能是在装有( )的袋子里摸的。A、10个红球 B、8 个红球、2个蓝球 C、10个蓝球 D、2个红球、8个蓝球
-
14、某校举办“我知浙江”知识竞赛活动，题目内容有如下几种类型。下面是50 名同学随机抽取试题的情况。
试卷类型
浙江生态
浙江交通
浙江物产
浙江经济
人次
24
3
14
9
根据表中的数据推测，类型试题可能最多，类型试题可能最少。
-
15、有A、B、C三种字母卡片共10张(有4张已填好)，将它们放入袋中随意摸一张，为使摸到A、B、C的可能性均不相等，且摸到A的可能性最大，摸到C的可能性最小，请你填一填。
-
16、 五年级举行数学转盘我“慧”玩的活动，小新和程程也加入到活动中来。他们约定：指针停在白色区域，小新赢；指针停在蓝色区域，程程赢。
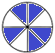(1)、如果只转一次转盘，程程一定会赢吗？请写出你的想法。(2)、请你在转盘上重新设计一下，使游戏公平。
-
17、箱子里放了若干个球，每种颜色的球数量各不相同。任意摸一个，要使摸到黄球的可能性最大，摸到绿球的可能性最小，还可能摸到蓝球，箱子里至少放( )个球。A、3 B、4 C、5 D、6
-
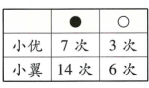
18、小优和小翼每次从同一盒子里任意摸出一个围棋棋子，记录后放回摇匀。小优摸了10次，小翼摸了20 次，摸出结果如表所示。根据表中的数据推测，他们最可能是从( )盒中摸的。
A、4个
B、3个 ， 1个
C、2个 ， 2个
D、1个 ， 3个
-
19、如图每个袋里都只有5 个红球。如果从袋里任意摸出一个球，那么从号袋里最难摸到红球；从号袋里一定能摸到红球。
-
20、袋子里有3个白球，6个红球，1个黄球，任意摸出一个球，摸到球的可能性最大，摸到球的可能性最小。要想摸出黄球和红球的可能性一样大，需增加个黄球或减少个红球。