相关试卷
-
1、在中,内角的对边分别是 , 满足.若 , 则的面积的最大值是.
-
2、已知随机变量服从正态分布 , 且 , 则.
-
3、平面直角坐标系中,定义为两点 , 的“切比雪夫距离”;又设点及直线上任意一点 , 称的最小值为点到直线的“切比雪夫距离”,记作.则下列结论正确的是( )A、当时, B、当时, C、对任意三点恒成立 D、动点与定点满足的轨迹围成的面积是16
-
4、如图所示,在平面直角坐标系中,以轴非负半轴为始边的锐角与钝角的终边与单位圆分别交于两点.若点的横坐标为 , 点的纵坐标为 , 则下列结论正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、每年4月23日为“世界读书日”,某学校于四月份开展“书香润泽校园,阅读提升思想”主题活动,为检验活动效果,学校收集当年二至六月的借阅数据如下表:
二月
三月
四月
五月
六月
月份代码
1
2
3
4
5
月借阅量(百册)
4.9
5.1
5.5
5.7
5.8
根据上表,可得关于的经验回归方程为 , 则下列结论正确的是( )
A、 B、借阅量的下四分位数为5.7 C、与的线性相关系数 D、七月的借阅量一定不少于百册 -
6、已知函数及其导函数的定义域均为 , 记 , 若为偶函数,为奇函数,则下列结论一定正确的是( )A、 B、为偶函数 C、 D、
-
7、已知函数 , 若存在常数 , 使得恒成立,则实数的最小值是( )A、 B、 C、 D、
-
8、圆台的上、下底面的面积分别是 , , 侧面积是 , 则这个圆台的体积是( )A、 B、 C、 D、
-
9、复数(为虚数单位,)在复平面上对应的点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
10、设集合 , 若集合 , , 则集合( )A、 B、 C、 D、
-
11、箱子中装有4个红球,2个黄球(除颜色外完全相同),掷一枚质地均匀的骰子1次,如果点数为 , 则从该箱子中一次性取出个球.规定:依据个球中红球的个数,判定甲的得分 , 每一个红球记1分;依据个球中黄球的个数,判定乙的得分 , 每一个黄球记2分.比如:若一次性取出了2个红球,2个黄球,则判定甲得分 , 乙得分.则在1次掷骰子取球的游戏中,.
-
12、设维向量 , , 定义运算:.(1)、当时,若且 , , 试比较与的大小;(2)、已知 , 记且和均为的某一排列}.
(ⅰ)求 , ;
(ⅱ)若 , 求.(提示:.)
-
13、已知椭圆 , 点到椭圆上点的距离的最大值为.(1)、求椭圆的方程;(2)、若过定点的直线交椭圆于点 , , 设点 , 直线与直线交于直线上一点,求直线的方程.
-
14、已知函数.(1)、当时,讨论的单调性;(2)、当时,恒成立,求的取值范围;(3)、求证:当时,.
-
15、在1,2,3,…,7这7个自然数中,任取3个数.(1)、求这3个数中恰有1个是偶数的概率;(2)、设为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时的值是2).求随机变量的分布列及其数学期望.
-
16、如图,在直三棱柱中, , , .是的中点,是与的交点.
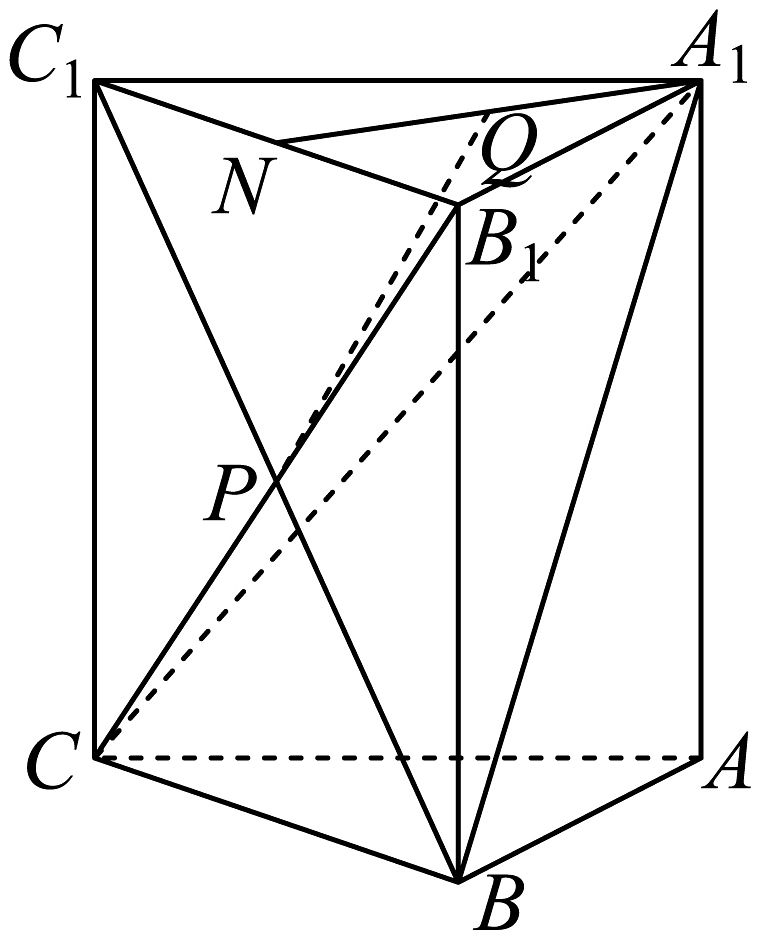 (1)、若是的中点,证明:平面;(2)、求与平面所成角的正弦值.
(1)、若是的中点,证明:平面;(2)、求与平面所成角的正弦值. -
17、关于的方程(且)有唯一实数解,其中为自然对数的底数,则实数的取值范围是.
-
18、在中, , , 则.
-
19、如图,在平行六面体中, , , , , , 为中点,在线段上(包含端点),则下列说法正确的是( )
 A、存在点 , 使得平面 B、存在点 , 使得平面平面 C、不存在点 , 使得 D、不存在点 , 使得四棱锥有内切球
A、存在点 , 使得平面 B、存在点 , 使得平面平面 C、不存在点 , 使得 D、不存在点 , 使得四棱锥有内切球 -
20、国家知识产权局信息显示,华为技术有限公司申请一项名为“三进制逻辑门电路、计算电路、芯片及其电子设备”的专利,该项专利可以实现大幅度减少二进制逻辑电路的晶体管数量,降低电路的功耗,提高计算效率.该专利蕴含的数学背景是一种以3为基数,以 , , 为基本数码的计数体系(对称三进制):三进制数对应的十进制数为 , 其中 , , 为了记号的方便,我们用表示数码 , 比如 , , .下面选项正确的是( )A、 B、 C、若 , , , 则 D、存在唯一的 , 使得成立