版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、人脸识别就是利用计算机分析人脸视频或者图像，并从中提取出有效的识别信息，最终判别人脸对象的身份．在人脸识别中为了检测样本之间的相似度主要应用距离的测试，常用的测量距离的方式有曼哈顿距离和余弦距离．已知二维空间两个点 $A (x_{1}, y_{1})$ 、 $B (x_{2}, y_{2})$ ，则其曼哈顿距离为 $d (A, B) = |x_{1} - x_{2}| + |y_{1} - y_{2}|$ ，余弦相似度为 $\cos (A, B) = \frac{x_{1}}{\sqrt{x_{1}^{2} + y_{1}^{2}}} \times \frac{x_{2}}{\sqrt{x_{2}^{2} + y_{2}^{2}}} + \frac{y_{1}}{\sqrt{x_{1}^{2} + y_{1}^{2}}} \times \frac{y_{2}}{\sqrt{x_{2}^{2} + y_{2}^{2}}}$ ，余弦距离为 $1 - \cos (A, B)$ ．已知 $0 < α < β < \frac{π}{2}$ ， $M (13 \cos α, 13 \sin α)$ 、 $N (8 \cos β, 8 \sin β)$ 、 $P (13 \cos (α + β), 13 \sin (α + β))$ 、 $Q (5 \cos 2 β, 5 \sin 2 β)$ ，若 $\cos (M, P) = \frac{3}{5}$ ， $\cos (M, N) = \frac{12}{13}$ ，则 $d (M, Q) =$ ．

查看解析
2、在 $△ A B C$ 中， $D$ 是 $B C$ 的中点， $A D = 2 \sqrt{2}$ ， $\cos ∠ A C B = \frac{\sqrt{5}}{5}$ ， $∠ A D C =45 °$ ，则 $A B =$ ．

查看解析
3、已知向量 $\vec{a} = (- 1, \sqrt{3})$ ， $\vec{b} = (4, 0)$ ，则向量 $\vec{a}$ 在向量 $\vec{b}$ 上的投影向量的坐标为．

查看解析
4、已知函数 $f (x)$ 的定义域为 $R$ ， $f (x + 2) + f (x) = f (2024)$ ， $f (\frac{1}{2} x + 1)$ 为奇函数，且 $f (\frac{3}{2}) = - \frac{1}{2}$ ，则（）

A、 $f (x + 4) = f (x)$ B、 $f (2024) = 1$ C、函数 $f (x)$ 是偶函数 D、 $\sum_{n = 1}^{2026} n f (n - \frac{1}{2}) = - \frac{1}{2}$ （参考公式： $\sum_{i = 1}^{n} g (i) = g (1) + g (2) + g (3) + \dots + g (n)$ ）

查看解析
5、已知圆台的上、下底面半径分别为1和3，母线长为 $2 \sqrt{2}$ ，则（）

A、圆台的母线与底面所成的角为 $45 °$ B、圆台的侧面积为 $8 \sqrt{2} π$ C、圆台的体积为 $\frac{14}{3} π$ D、若圆台的两个底面的圆周在同一个球的球面上，则该球的表面积为 $40 π$

查看解析
6、下列说法正确的是（）

A、若 $a > b$ ， $c > d$ ，则 $a - d > b - c$ B、若 $a < |b|$ ，则 $a^{2} < b^{2}$ C、若 $a > 0$ ， $b > 0$ ， $a + b = 1$ ，则 $\frac{1}{a} + \frac{1}{b}$ 的最小值为4 D、若 $a > 0$ ， $b > 0$ ， $a b + a + b = 8$ ，则 $a + b$ 的最小值为4

查看解析
7、某工业园区有 $A$ 、 $B$ 、 $C$ 共3个厂区，其中 $A B = 6 \sqrt{3} km$ ， $B C = 10 km$ ， $∠ A B C = 90 °$ ，现计划在工业园区内选择 $P$ 处建一仓库，若 $∠ A P B = 120 °$ ，则 $C P$ 的最小值为（）

A、 $6 km$ B、 $8 km$ C、 $4 \sqrt{3} km$ D、 $6 \sqrt{2} km$

查看解析
8、函数 $f (x) = \sin (ω x + \frac{π}{3}) (ω > 0)$ 的图象在区间 $(0, 1)$ 上恰有一条对称轴和一个对称中心，则（）

A、 $ω \in (\frac{2 π}{3}, \frac{7 π}{6}]$ B、当 $ω = π$ 时， $f (x)$ 在区间 $(\frac{1}{2}, 1)$ 上不单调 C、 $f (x)$ 在区间 $(0, 1)$ 上无最大值 D、 $f (x)$ 在区间 $(0, 1)$ 上的最小值为 $- 1$

查看解析
9、“ $a < 3$ ”是“函数 $f (x) = \log_{2} [(3 - a) x - 1]$ 在区间 $(1, + \infty)$ 上单调递增”的（）

A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件

查看解析
10、集合 $A, B$ 满足 $A \cup B = \{1, 3, 5, 7, 9\}$ ， $A \cap B = \{1, 7\}$ ， $A = \{1, 5, 7\}$ ，则集合 $B$ 中的元素个数为（）

A、3 B、4 C、5 D、6

查看解析
11、若数列 $\{a_{n}\} (1 \leq n \leq k, n \in N^{*}, k \in N^{*})$ 满足 $a_{n} \in \{0, 1\}$ ，则称数列 $\{a_{n}\}$ 为 $k$ 项 $0 - 1$ 数列，由所有 $k$ 项 $0 - 1$ 数列组成集合 $M_{k}$ .

(1)、若 $\{a_{n}\}$ 是12项0 $- 1$ 数列，当且仅当 $n = 3 p (p \in N^{*}, p \leq 4)$ 时， $a_{n} = 0$ ，求数列 $\{{(- 1)}^{n} a_{n}\}$ 的所有项的和；

(2)、从集合 $M_{k}$ 中任意取出两个数列 $\{a_{n}\}, \{b_{n}\}$ ，记 $X = \sum_{i = 1}^{k} |a_{i} - b_{i}|$ .
①求随机变量 $X$ 的分布列，并证明： $E (X) > \frac{k}{2}$ ；
②若用某软件产生 $k (k \geq 2)$ 项 $0 - 1$ 数列，记事件 $A =$ “第一次产生数字1”， $B =$ “第二次产生数字1”，且 $0 < P (A) < 1, 0 < P (B) < 1$ .若 $P (B ∣ A) < P (B ∣ \bar{A})$ ，比较 $P (A ∣ B)$ 与 $P (A ∣ \bar{B})$ 的大小.

查看解析
12、一个袋子中有10个大小相同的球，其中红球7个，黑球3个.每次从袋中随机摸出1个球，摸出的球不再放回.设第1，2，3次都摸到红球的概率为 $P_{1}$ ；在第1，2次都摸到红球的条件下，第3次摸到红球的概率为 $P_{2}$ .求 $P_{1} + P_{2} =$ .

查看解析
13、为弘扬我国古代的“六艺文化”，某校计划在社会实践中开设“礼”、“乐”、“射”、“御”、“书”、“数”六门体验课程，每天开设一门，连续开设6天，则下列结论正确的是（）

A、从六门课程中选两门的不同选法共有20种 B、课程“数”不排在最后一天的不同排法共有600种 C、课程“礼”、“书”排在相邻两天的不同排法共有240种 D、课程“乐”、“射”、“御”排在都不相邻的三天的不同排法共有72种

查看解析
14、列奥纳多 $\cdot$ 达 $\cdot$ 芬奇（Leonardo da Vinci，1452-1519）是意大利文艺复兴三杰之一．他曾提出：固定项链的两端，使其在重力的作用下自然下垂，项链所形成的曲线是什么？这就是著名的“悬链线问题”，后人给出了悬链线的函数表达式 $φ (x) = a \cosh \frac{x}{a}$ ，其中 $a$ 为悬链线系数， $\cosh x$ 称为双曲余弦函数，其函数表达式为 $\cosh x = \frac{e^{x} + e^{- x}}{2}$ ，相反地，双曲正弦函数的函数表达式为 $\sinh x = \frac{e^{x} - e^{- x}}{2}$ ．

(1)、证明： $\cosh^{2} x - \sinh^{2} x = 1$ ；

(2)、求不等式： $\sinh (2 x - 1) + \sinh (x - 2) < 0$ 的解集；

(3)、函数 $f (x) = 2 m \cosh (2 x) - 2 \sinh (x) - 3$ 的图象在区间 $[0, \ln 2]$ 上与 $x$ 轴有2个交点，求实数 $m$ 的取值范围．

查看解析
15、已知函数 $f (x)$ 为奇函数，且当 $x > 0$ 时， $f (x) = x^{2} - 1$ ，则 $f (- 2) =$ （）

A、 $- \frac{5}{4}$ B、 $- \frac{3}{4}$ C、 $- 3$ D、3

查看解析
16、如图，一个底面半径为2dm，母线长为 $2 \sqrt{5} dm$ 的圆锥形封闭透明容器内部装有一种液体，当圆锥底面向下平放在水平桌面上时，液面的高度恰好为圆锥的高的 $\frac{1}{2}$ ，则当圆锥的顶点在桌面上，且底面平行于水平桌面时，液面的高度为（）

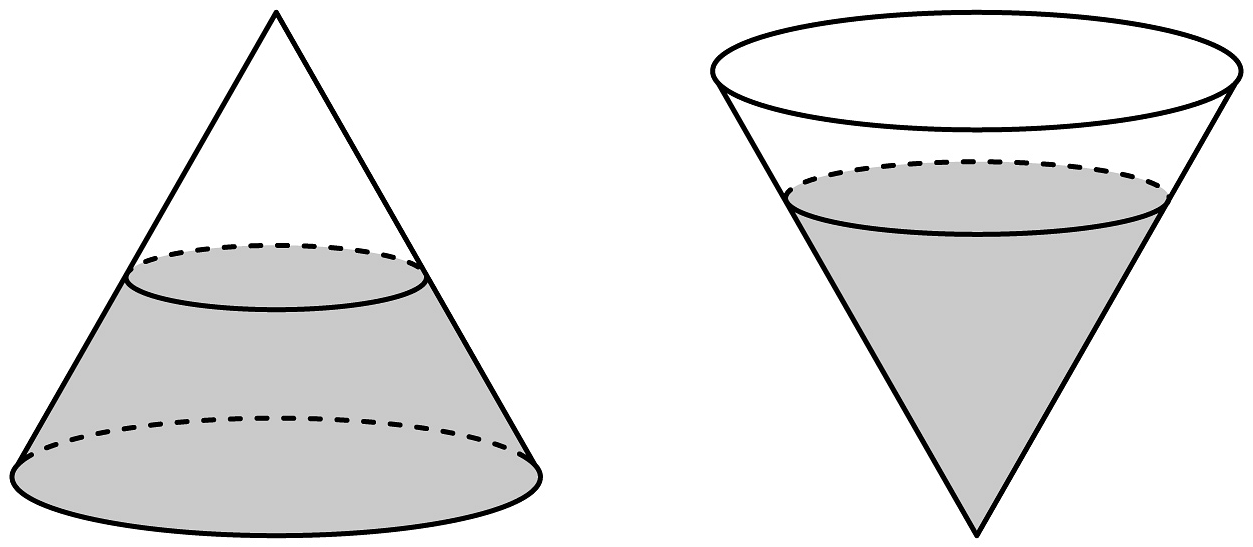A、 $\sqrt[3]{7} dm$ B、2dm C、3dm D、 $2 \sqrt[3]{7} dm$

查看解析
17、已知 $a > 0$ ， $b > 0$ ，则下列说法正确的是（）

A、若 $a + b = 1$ ，则 ${log}_{2} a + {log}_{2} b \leq - 2$ B、若 $a + b = 1$ ，则 $\sqrt{a} + \sqrt{b} < 1$ C、若 $a - b = 1$ ，则 $2^{a} - \frac{1}{2^{b}} > 1$ D、若 $a - b = 1$ ，则 $a^{2} + b^{2} > 1$

查看解析
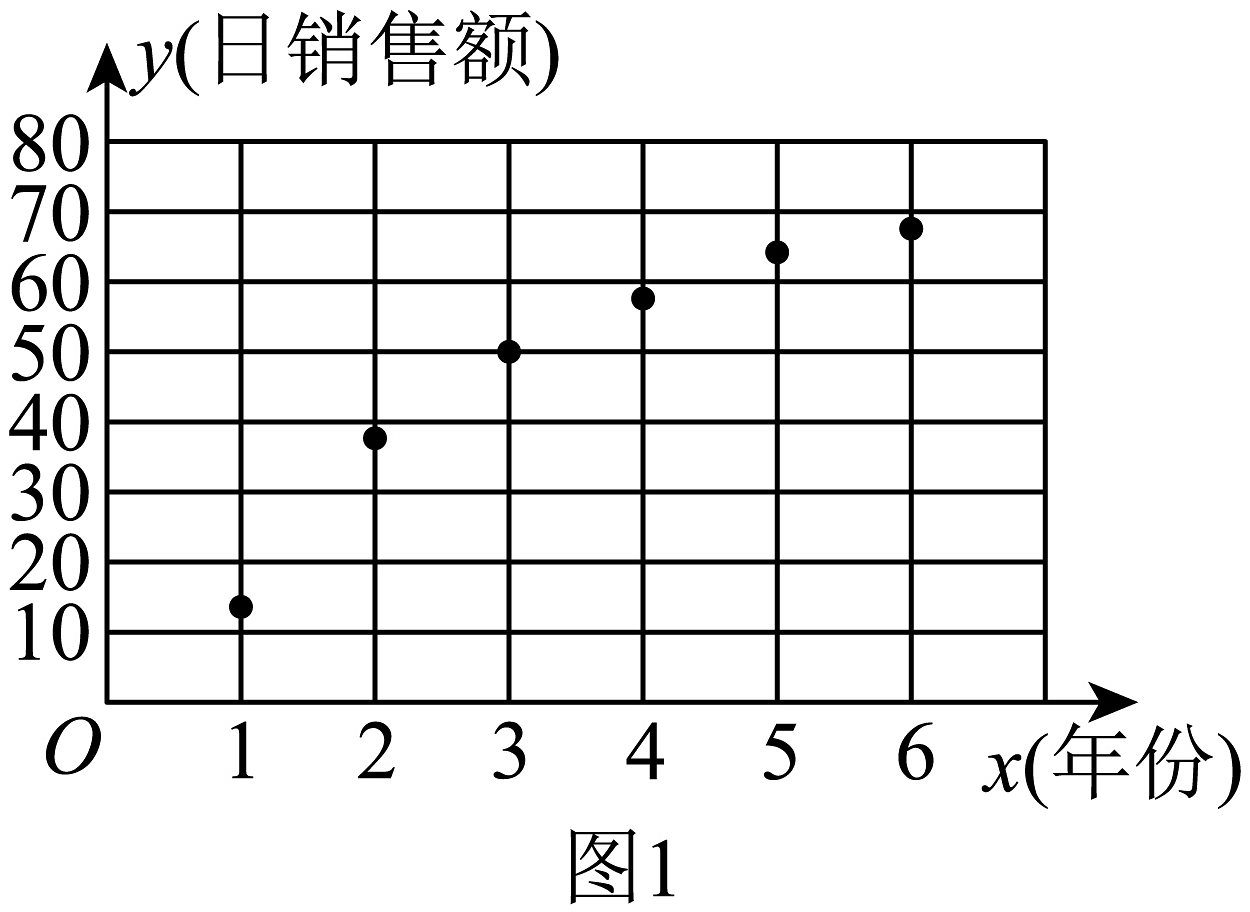
18、一年一度的“双11”促销活动落下帷幕，各大电商平台发布的数据显示，在消费品以旧换新、家电政府补贴等促消费政策和活动的带动下，消费市场潜能加速释放，带动相关商品销售保持增长. 经过调研，得到2019年到2024年“双11”活动当天某电商平台线上日销售额 $y$ （单位：百亿元）与年份（第 $x$ 年）的6组数据（时间变量 $x$ 的取值依次为 $1, 2, \cdot \cdot \cdot, 6$ ），对数据进行处理，得到如下散点图（图1）及一些统计量的值. 其中 $t_{i} = \ln x_{i}, \bar{t} = \frac{1}{6} \sum_{i = 1}^{6} t_{i}$ .
$\bar{y}$
$\bar{x}$
$\sum_{i = 1}^{6} x_{i}^{2}$
$\sum_{i = 1}^{6} x_{i} y_{i}$
$\bar{t}$
$\sum_{i = 1}^{6} t_{i}^{2}$
$\sum_{i = 1}^{n} t_{i} y_{i}$
48.7
3.5
91
1204
1.1
9.4
388.1
分别用两种模型：① $y = b x + a$ ；② $y = b \ln x + a$ 进行拟合，得到相应的回归方程，并进行残差分析，得到如图所示的残差图（图2）（残差值 $=$ 真实值 $-$ 预测值）.

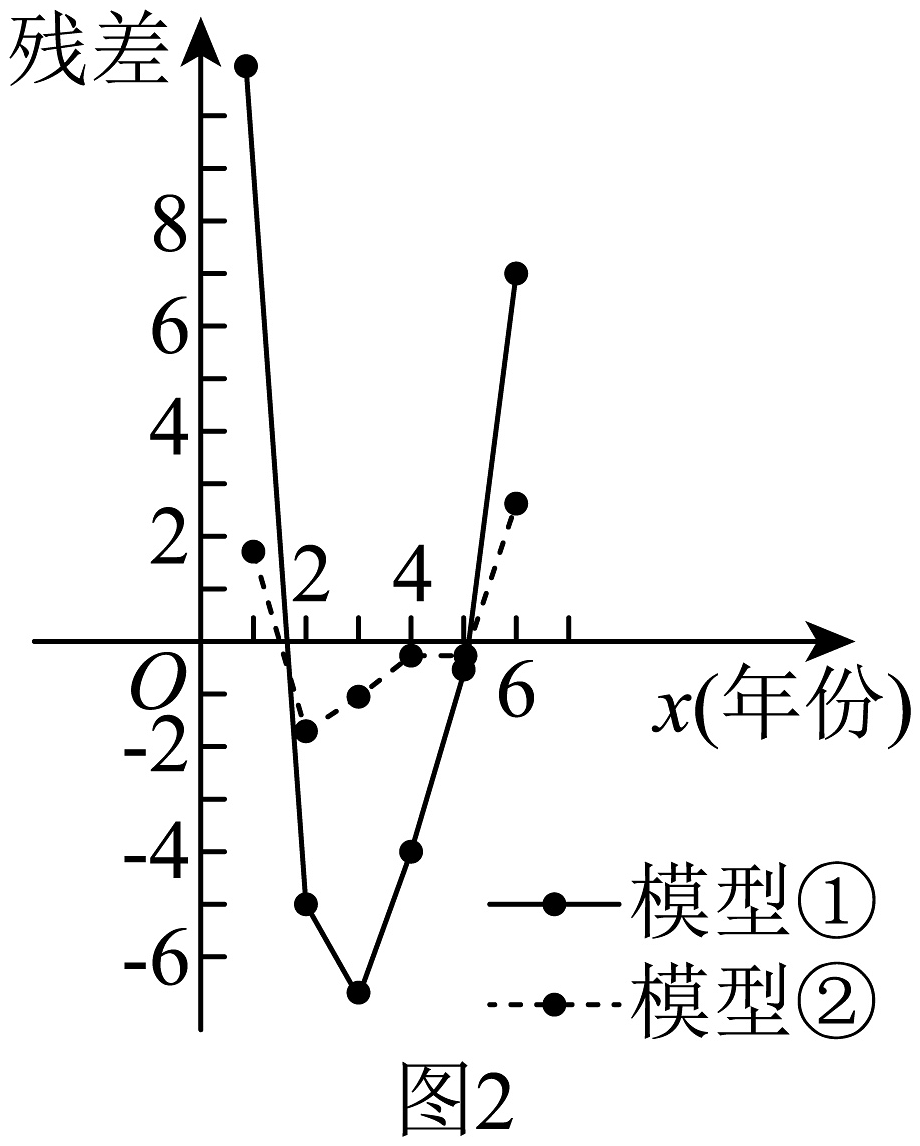(1)、根据题中信息，通过残差图比较模型①，②的拟合效果，应选择哪一个模型进行拟合？请说明理由；

(2)、根据（1）中所选模型，
（i）求出 $y$ 关于 $x$ 的经验回归方程（系数精确到0.1）；
（ⅱ）若该电商平台每年活动当天线上日销售额 $y$ 与当日营销成本 $u$ 及年份 $x$ 存在线性关系： $y = 3 u + 2.6 x$ ，则在第几年活动当日营销成本的预测值最大?
参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}, \hat{a} = \bar{y} - \hat{b} \bar{x}$ ；参考数据： $\ln 7 \approx 1.95$ .

查看解析
19、已知 $cos (x - \frac{π}{10}) = - \frac{4}{5}$ ，则 $sin (2 x + \frac{3 π}{10}) =$ .

查看解析
20、微分中值定理是微积分学中的重要定理，它是研究区间上函数值变化规律的有效工具，其中拉格朗日中值定理是核心，它的内容如下：
如果函数 $f (x)$ 在闭区间 $[a, b]$ 上连续，在开区间 $(a, b)$ 可导，导数为 $f^{'} (x)$ ，那么在开区间 $(a, b)$ 内至少存在一点 $c$ ，使得 $f^{'} (c) = \frac{f (b) - f (a)}{b - a}$ ，其中 $c$ 叫做 $f (x)$ 在 $[a, b]$ 上的“拉格朗日中值点”.已知函数 $f (x) = \frac{(a + 1) x^{2}}{4} \ln x + b^{2} (x - 4) e^{a x} - \frac{b^{2}}{6} x^{3} + (\frac{9 b + 15}{8}) x^{2}$ .

(1)、若 $a = - 1, b = 0$ ，求函数 $f (x)$ 在 $[1, 7]$ 上的“拉格朗日中值点” $x_{0}$ ；

(2)、若 $a = - 1, b = 1$ ，求证：函数 $f (x)$ 在区间 $(0, + \infty)$ 图象上任意两点 $A$ ， $B$ 连线的斜率不大于 $18 - e^{- 6}$ ；

(3)、若 $a = 1, b = - 1, \forall x_{1}, x_{2}, x_{3} \in (\frac{1}{4}, 1)$ ，且 $x_{1} < x_{2} < x_{3}$ ，求证： $\frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} > \frac{f (x_{3}) - f (x_{2})}{x_{3} - x_{2}}$ .

查看解析

上一页 989 990 991 992 993 下一页跳转

$\bar{y}$	$\bar{x}$	$\sum_{i = 1}^{6} x_{i}^{2}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\bar{t}$	$\sum_{i = 1}^{6} t_{i}^{2}$	$\sum_{i = 1}^{n} t_{i} y_{i}$
48.7	3.5	91	1204	1.1	9.4	388.1