相关试卷
-
1、如图,在正四棱台中, , , , 棱上的点满足取得最小值.
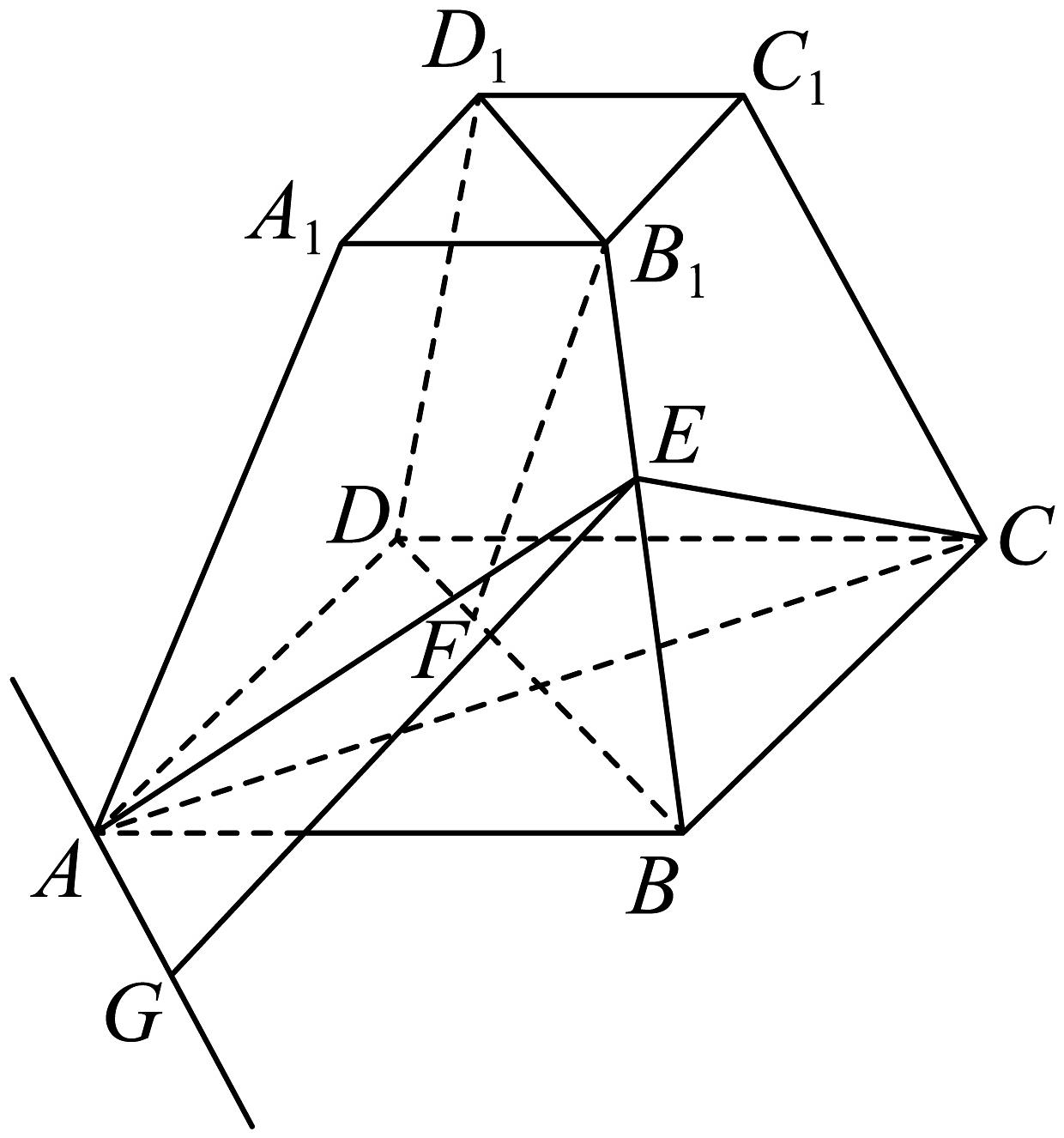 (1)、证明:平面;(2)、在空间取一点为 , 使得 , 设平面与平面的夹角为 , 求的值.
(1)、证明:平面;(2)、在空间取一点为 , 使得 , 设平面与平面的夹角为 , 求的值. -
2、已知首项为1的等差数列的公差为2,又数列满足.(1)、求数列的前项和;(2)、在中,内角的对边分别为 , 且 , , 求面积的最大值.
-
3、已知某批矿物晶体中含有大量水分子,且经过测量发现其中轻水分子,重水分子,超重水分子的比例为.(1)、现利用仪器从一块矿物晶体中分离出3个水分子,用频率估计概率,求至少分离出2个轻水分子的概率;(2)、从一块矿物晶体中分离出10个水分子,其中轻水分子的个数有6个,然后再从这10个水分子中随机分离出3个水分子来进行后续的实验,记这3个水分子中轻水分子的个数为 , 求的数学期望.
-
4、已知椭圆与圆有四个不同的公共点,其中.若 , 则的最大值为.
-
5、已知二项式的展开式中的常数项为 , 则.
-
6、已知 , , 若 , 则.
-
7、某箱中有若干个编号依次为的球,每个球除编号外完全相同.现从箱中每次不放回地取一个球,若第次取出球的编号为 , 则记为 , 则下列说法正确的是( )A、若则 B、若则 C、若则事件和事件相互独立 D、若则事件和事件相互独立
-
8、已知正数满足 , 则( )A、 B、 C、 D、
-
9、若则的最小值为( )A、 B、10 C、 D、2
-
10、已知 , , , 则( )A、 B、 C、 D、
-
11、已知半径为3,高为1的圆锥底面圆周上的点和顶点均在球的表面上,则球的体积为( )A、 B、 C、 D、
-
12、已知是关于的方程的一个根,则( )A、 B、0 C、1 D、20
-
13、已知曲线过抛物线的焦点,则的准线方程为( )A、 B、 C、 D、
-
14、已知命题 , ;命题 , 是质数,则( )A、均是真命题 B、均是真命题 C、均是真命题 D、均是真命题
-
15、已知函数.(1)、求函数的定义域;(2)、判断并证明函数的奇偶性;(3)、求不等式的解集.
-
16、已知双曲线的一条渐近线的方程为 , 则C的离心率的值为.
-
17、设椭圆的左右焦点为 , 右顶点为 , 已知点在椭圆上,若 , 则椭圆的离心率为( )A、 B、 C、 D、
-
18、若 , 则( )A、 B、 C、 D、
-
19、奇函数和偶函数的图象分别如图1、图2所示,方程和的实根个数分别 , , 则( )
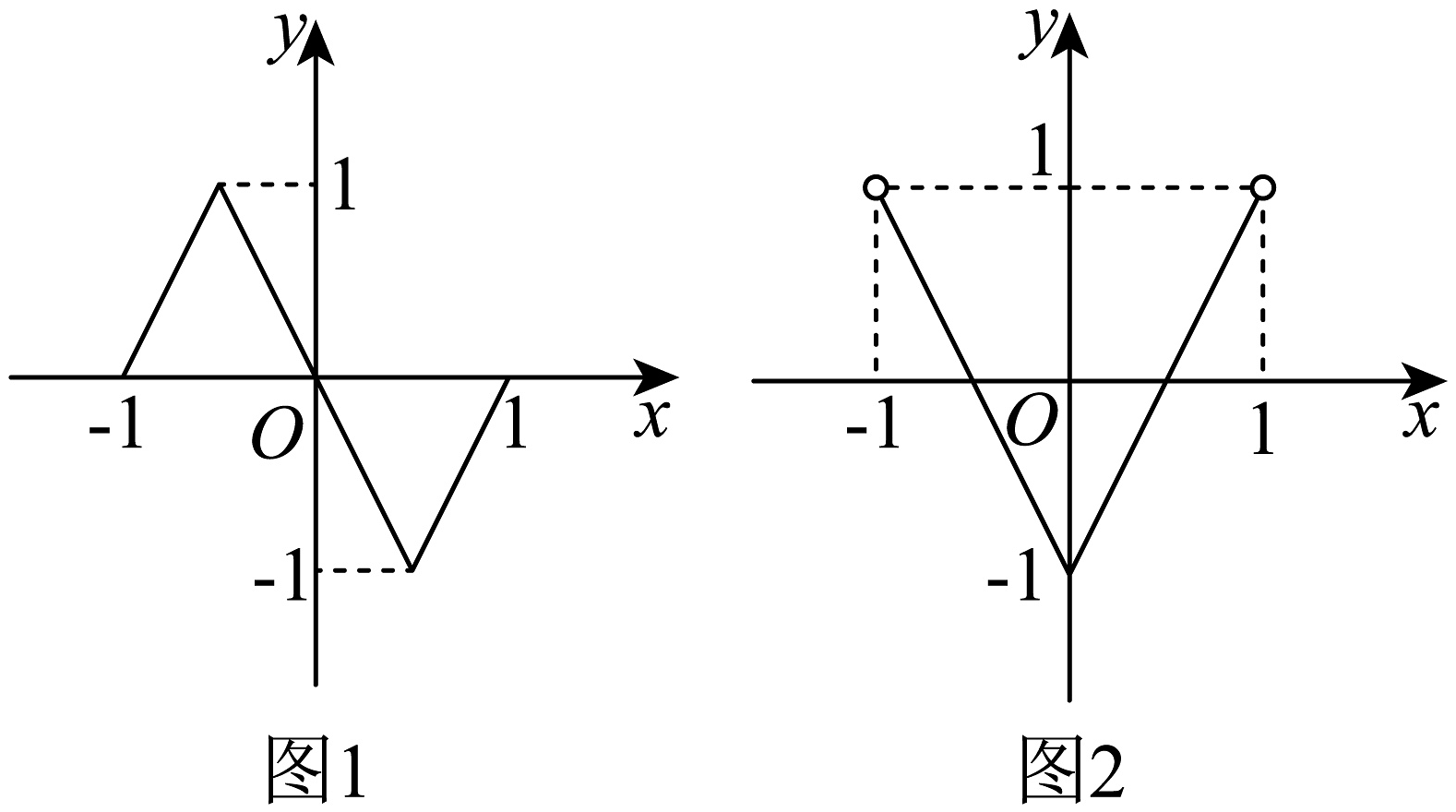 A、3 B、7 C、10 D、14
A、3 B、7 C、10 D、14 -
20、已知函数.(1)、若曲线在处的切线方程为 , 求实数的值;(2)、若对于任意 , 恒成立,求实数的取值范围.