相关试卷
-
1、如图,在四棱锥中,平面平面 , 四边形是边长为的正方形,为等边三角形,点是线段的中点,点满足 .
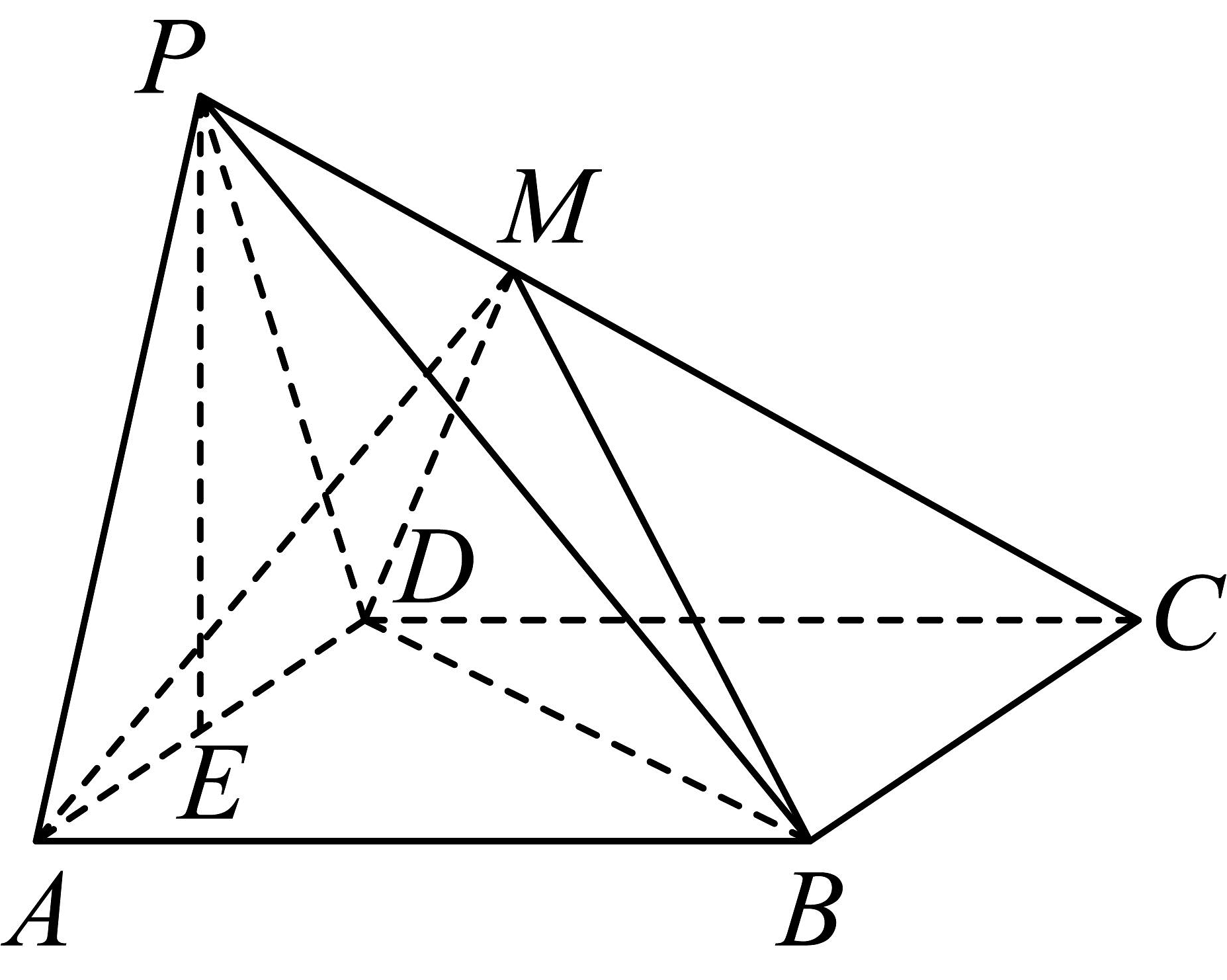 (1)、求证:平面﹔(2)、求二面角的余弦值.
(1)、求证:平面﹔(2)、求二面角的余弦值. -
2、已知函数.(1)、若函数在区间上单调,求实数的取值范围;(2)、若对于任意的总存在 , 使得成立,求实数的取值范围.
-
3、某中学为了解高中数学学习中抽象思维与性别的关系,随机抽取了男生120人,女生80人进行测试.根据测试成绩按分组得到如图所示的频率分布直方图,并且男生的测试成绩不小于60分的有80人.
 (1)、填写下面的列联表,判断是否有的把握认为高中数学学习中抽象思维与性别有关;
(1)、填写下面的列联表,判断是否有的把握认为高中数学学习中抽象思维与性别有关;成绩小于60
成绩不小于60
合计
男
女
合计
(2)、规定成绩不小于60(百分制)为及格,按及格和不及格用分层抽样,随机抽取10名学生进行座谈,再在这10名学生中选2名学生发言,设及格学生发言的人数为 , 求的分布列和期望.附:
0.10
0.050
0.010
2.706
3.841
6.635
-
4、集合 , .(1)、用区间表示集合A;(2)、若 , , 求a,b的取值范围.
-
5、已知函数满足对任意 , 都有成立,则的取值范围是.
-
6、若的展开式中的系数为 , 则展开式中所有项的二项式系数之和为 . (以数字作答)
-
7、一圆锥的侧面展开图如图所示, , 弧长为 , 为线段的中点,为弧中点,则( )
 A、该圆锥的体积为 B、在扇形中, C、该圆锥内半径最大的球的表面积为 D、该圆锥内接正四棱柱表面积的最大值为
A、该圆锥的体积为 B、在扇形中, C、该圆锥内半径最大的球的表面积为 D、该圆锥内接正四棱柱表面积的最大值为 -
8、下列命题中正确的是( )A、设m为直线, , 为平面,且 , 则“”是“”的充要条件 B、设随机变量 , 若 , 则 C、若不等式恒成立,则m的取值范围是 D、已知直线经过点 , 则的取值范围是
-
9、下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则
-
10、已知函数 , 存在最小值,则实数的取值范围为( )A、 B、 C、 D、
-
11、若 , 则函数有零点的概率为A、 B、 C、 D、
-
12、函数的图象大致是( )A、
 B、
B、 C、
C、 D、
D、
-
13、下列关系中,表述正确的是( )A、 B、
 A
C、
D、
A
C、
D、
-
14、下列函数中,既是偶函数,又在上单调递增的有( )A、 B、 C、 D、
-
15、如图,在四棱锥中,平面平面 , , , , .
 (1)、求证:平面平面;(2)、若 , , 点是线段上一点,且二面角的余弦值为 , 求的值.
(1)、求证:平面平面;(2)、若 , , 点是线段上一点,且二面角的余弦值为 , 求的值. -
16、函数的大致图象是( )A、
 B、
B、 C、
C、 D、
D、
-
17、如图,在八面体中,四边形是边长为2的正方形,平面平面 , 二面角与二面角的大小都是 , , .
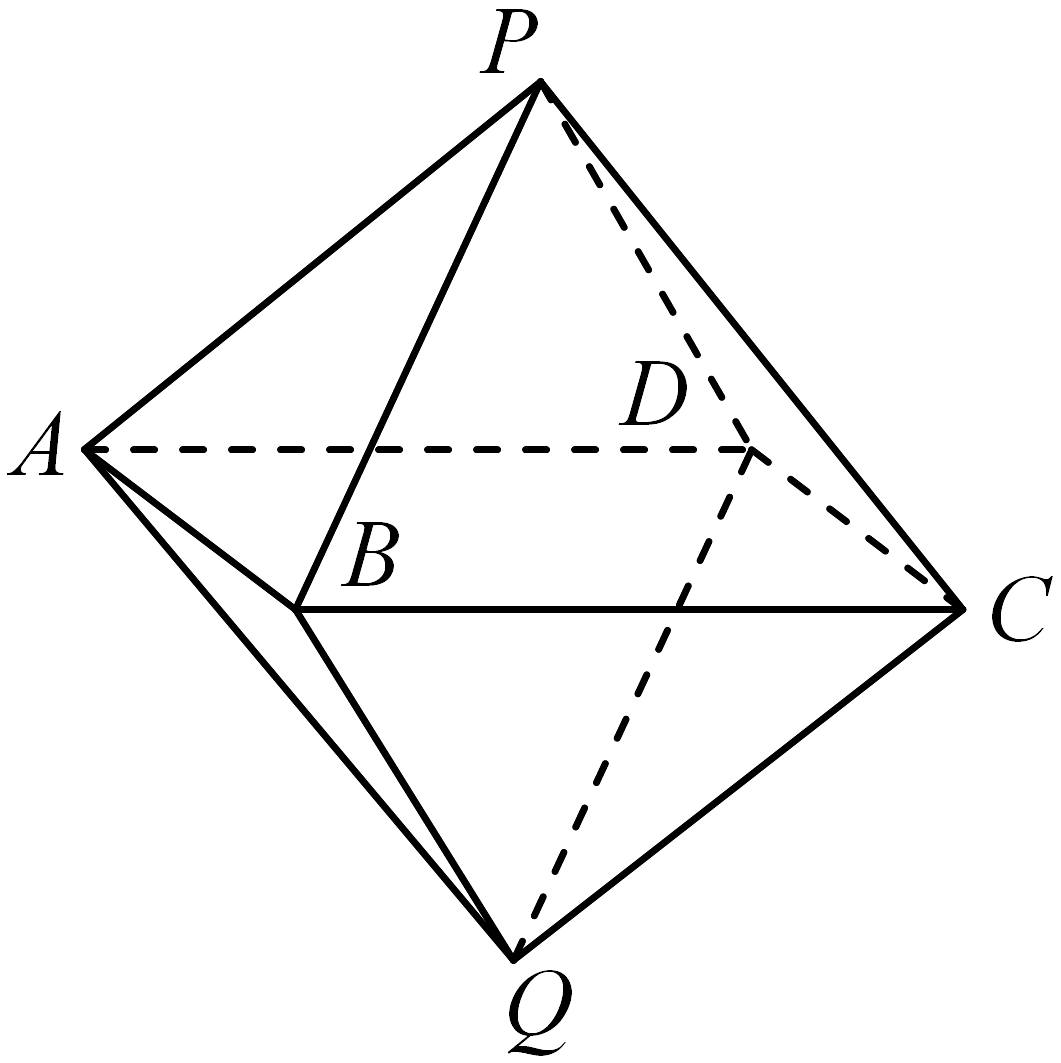 (1)、证明:平面平面;(2)、设为的重心,是否在棱上存在点 , 使得与平面所成角的正弦值为 , 若存在,求到平面的距离,若不存在,说明理由.
(1)、证明:平面平面;(2)、设为的重心,是否在棱上存在点 , 使得与平面所成角的正弦值为 , 若存在,求到平面的距离,若不存在,说明理由. -
18、已知函数满足 , 且 , 当时, . 函数 .(1)、求实数的值;(2)、当时,求的解析式;(3)、设 , 是否存在实数 , 使不等式在时恒成立?若存在,求实数的取值范围;若不存在,请说明理由.
-
19、某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数与时刻(时)的关系为 , , 其中是与气象有关的参数,且 , 若用每天的环境综合污染指数的最大值作为当天的综合污染指数,并记作 .(1)、当时,求环境综合污染指数的值域;(2)、求的解析式;(3)、规定当时为综合污染指数超标,求当在什么范围内时,该市市中心的综合污染指数超标.
-
20、已知的三个内角所对的边分别为 , 满足 .(1)、求;(2)、若为锐角三角形,且 , 求的周长的取值范围.