相关试卷
-
1、如图,已知直四棱柱的所有棱长均相等, , 是棱AB的中点,设平面 , 经过直线 , 且平面 , 平面 , 若平面 , 则异面直线与所成角的余弦值为.

-
2、已知函数 , 当时,函数的零点为.
-
3、已知 , , 设 , 的夹角为 , 则的最小值为.
-
4、如图,在矩形ABCD中, , , 沿矩形对角线BD将折起形成四面体ABCD,在这个过程中,下列结论正确的是( )
 A、在四面体ABCD中,当时, B、四面体ABCD的体积的最大值为 C、在四面体ABCD中,BC与平面ABD所成的角可能为 D、四面体ABCD的外接球的半径为定值
A、在四面体ABCD中,当时, B、四面体ABCD的体积的最大值为 C、在四面体ABCD中,BC与平面ABD所成的角可能为 D、四面体ABCD的外接球的半径为定值 -
5、某电视台的夏日水上闯关节目一共有三关,第一关与第二关的过关率分别为 , , 只有通过前一关才能进入下一关,每一关都有两次闯关机会,且通过每关相互独立.一选手参加该节目,则下列结论正确的是( )A、该选手闯过第一关的概率为 B、该选手单独闯过第二关的概率为 C、该选手能进入第三关的概率为 D、该选手能进入第三关的概率为
-
6、在中,内角A,B,C所对的边分别是a,b,c,则( )A、若 , 则 B、若是单位圆的内接三角形,则 C、若 , 则 D、若 , 则是锐角三角形
-
7、在中, , , , 若 , 则等于( )A、7 B、8 C、12 D、13
-
8、在三棱锥中,平面 , , .若 , A,B,C,D四点都在球的表面上,则球的表面积为( )A、 B、 C、 D、
-
9、已知外接圆的圆心为 , 半径为1,点到近的距离分别为 , , .若 , 则( )A、 B、1 C、 D、2
-
10、某湖中有一小岛 , 沿湖有一条正南方向的公路,一辆汽车在公路处测得小岛在南偏西的方向上,汽车行驶2公里到达处后,又测得小岛在南偏西的方向上,如图所示,则小岛到公路的距离为( )
 A、公里 B、公里 C、公里 D、公里
A、公里 B、公里 C、公里 D、公里 -
11、已知为坐标原点, , , , 若为直线OC上一动点,当取最小值时,( )A、 B、 C、 D、
-
12、不透明的口袋中装有50个大小相同的红球、白球和黑球,其中红球有20个,从口袋中摸出一个球,若摸出白球的概率是0.2,则摸出黑球的概率是( )A、0.2 B、0.3 C、0.4 D、0.6
-
13、若棱长为的正方体的内切球的表面积为 , 则( )A、2 B、4 C、 D、
-
14、如图,已知全集 , 集合 , 则图中阴影部分表示的集合是( )
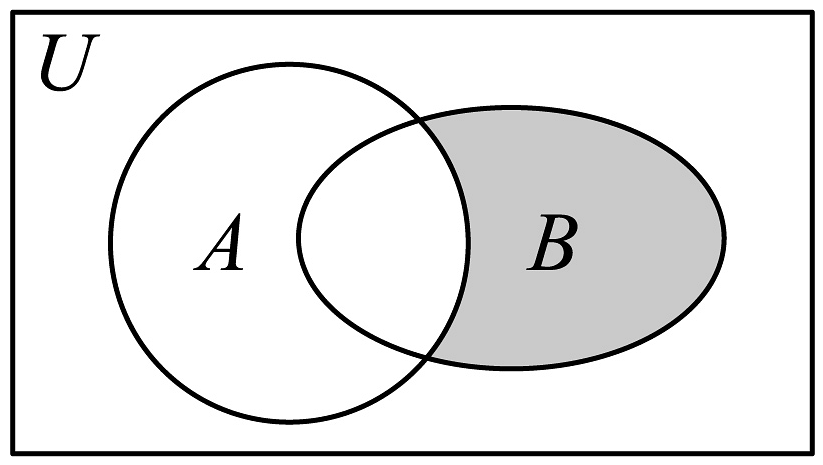 A、 B、 C、 D、
A、 B、 C、 D、 -
15、某学校为了解本校历史、物理方向学生的学业水平模拟测试数学成绩情况,分别从物理方向的学生中随机抽取60人的成绩得到样本甲,从历史方向的学生中随机抽取人的成绩得到样本乙,根据两个样本数据分别得到如下直方图:

已知乙样本中数据在的有10个.
(1)、求和乙样本直方图中的值;(2)、试估计该校物理方向的学生本次模拟测试数学成绩的平均值和历史方向的学生本次模拟测试数学成绩的中位数(同一组中的数据用该组区间中点值为代表);(3)、若本校历史方向的学生约为300人,估计其中数学成绩在85分以上的人数. -
16、一个圆锥的侧面展开图是半径为2,圆心角为的扇形,则该圆锥的表面积为 .
-
17、下列说法正确的是( )A、某人在玩掷骰子游戏,掷得数字5的概率是 , 则此人掷6次骰子一定能掷得一次数字5 B、为了了解全国中学生的心理健康情况,应该采用普查的方式 C、一组数据8,8,7,10,6,8,9的众数和中位数都是8 D、若甲组数据的方差 , 乙组数据的方差 , 则乙比甲稳定
-
18、已知是定义在上的奇函数,且若对任意的m, , , 都有.
(1)若 , 求实数a的取值范围;
(2)若不等式对任意和都恒成立,求实数t的取值范围.
-
19、已知关于x的函数y=(m+6)x2+2(m-1)x+m+1恒有零点.(1)、求m的范围;(2)、若函数有两个不同零点,且其倒数之和为-4,求m的值.
-
20、已知 , 是方程的两根,求下列各式的值.(1)、(2)、