相关试卷
-
1、函数在区间上的图象是一条连续不断的曲线,且满足 , 函数的图象关于点对称,则( )A、的图象关于点对称 B、8是的一个周期 C、一定存在零点 D、
-
2、已知函数的图象过点 , 且两条相邻对称轴之间的距离为 , 则下列说法正确的是( )A、 B、在上单调递增 C、直线为函数图象的一条对称轴 D、在上的值域为
-
3、几何学史上有一个著名的米勒问题:“设是锐角的一边上的两点,试在边上找一点 , 使得最大.”如图,其结论是:点为过两点且和射线相切的圆的切点.根据以上结论解决以下问题:在平面直角坐标系中,给定两点 , 点在轴上移动,则的最大值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、已知等差数列的前项和为 , 若 , 则( ).A、4 B、 C、 D、6
-
5、已知方程表示的曲线是椭圆,则实数的取值范围是( ).A、 B、 C、 D、
-
6、样本数据15,13,12,31,29,25,43,19,17,38的中位数为( ).A、19 B、22 C、21 D、18
-
7、已知椭圆:的左焦点为 , 椭圆上任意一点到的距离最大值为6.(1)、求椭圆的方程;(2)、过原点且斜率为的直线与椭圆交于M,N两点.
(i)当时,设直线 , 的斜率分别是 , , 求证:为定值;
(ⅱ)过点作垂直于的直线交于 , 交圆:于P,Q两点,记 , 的面积分别为 , 求的取值范围.
-
8、如图,在矩形纸片中, , , 沿将折起,使点D到达点P的位置,点P在平面的射影H落在边上.
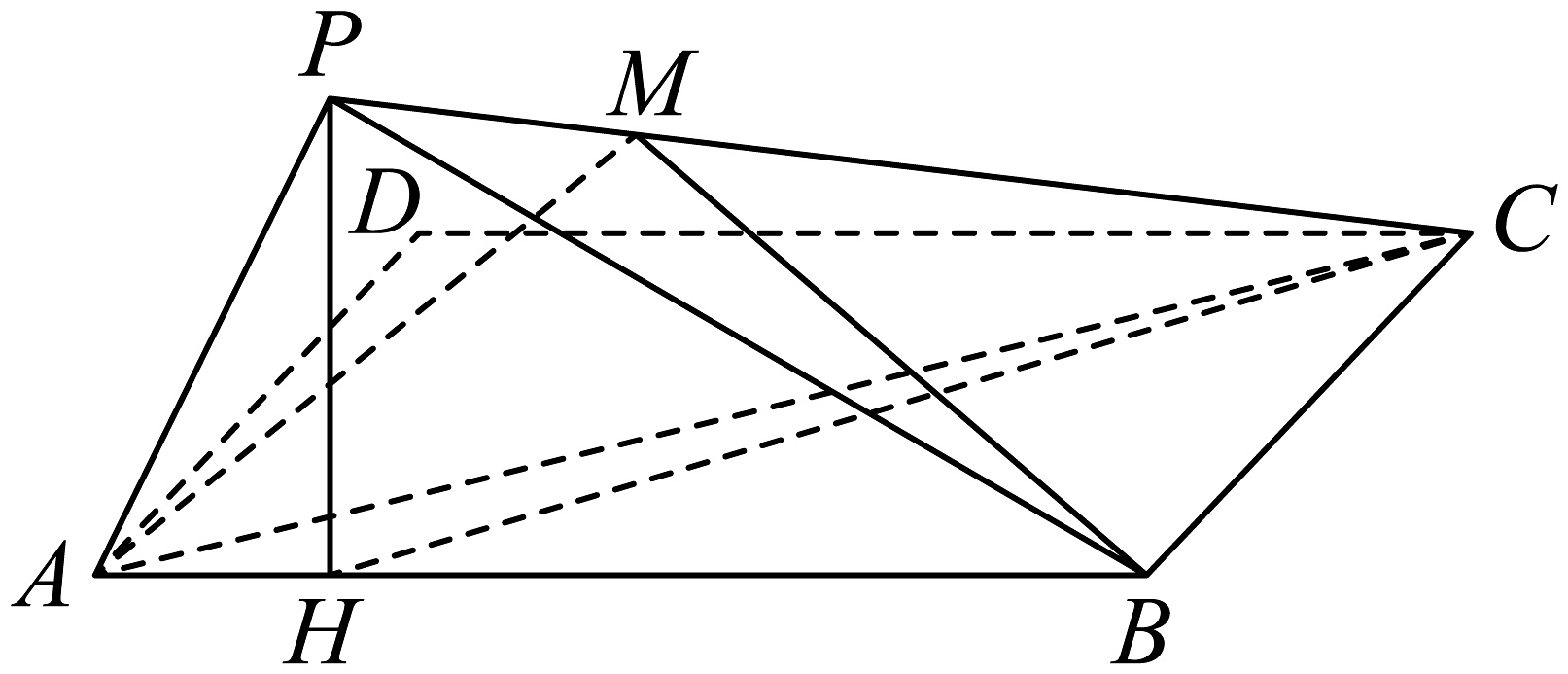 (1)、求三棱锥的体积;(2)、若M是棱上的一个动点,是否存在点M,使得平面与平面的夹角正切值为 , 若存在,求点M到平面的距离;若不存在,请说明理由.
(1)、求三棱锥的体积;(2)、若M是棱上的一个动点,是否存在点M,使得平面与平面的夹角正切值为 , 若存在,求点M到平面的距离;若不存在,请说明理由. -
9、已知函数.(1)、当时,求曲线在点处的切线方程;(2)、当时,设 , 讨论函数的单调性;(3)、若函数在上有且仅有2个零点,求实数的取值范围.
-
10、某汽车配件厂生产了一种塑胶配件,质检人员在这批配件中随机抽取了100个,将其质量指标值(单位:分)作为一个样本,得到如图所示的频率分布直方图.
 (1)、求的值;(2)、求这组数据的平均数(同一组中的数据用该组区间的中点值为代表);(3)、当配件的质量指标值不小于80分时,配件为“优秀品”,以频率估计概率.在这批产品中有放回地随机抽取3件产品,随机变量表示:抽得的产品为“优秀品”的个数,求的分布列及数学期望.
(1)、求的值;(2)、求这组数据的平均数(同一组中的数据用该组区间的中点值为代表);(3)、当配件的质量指标值不小于80分时,配件为“优秀品”,以频率估计概率.在这批产品中有放回地随机抽取3件产品,随机变量表示:抽得的产品为“优秀品”的个数,求的分布列及数学期望. -
11、记的内角A,B,C所对的边分别为a,b,c,且.(1)、求B;(2)、设D为边的中点,若 , , 求的面积.
-
12、已知圆的方程为 , 直线的方程为 , 直线被圆截得的弦中长度为整数的共有条.
-
13、在五一小长假期间,要从6人中选若干人在3天假期值班(每天只需1人值班),不出现同一人连续值班2天,则可能的安排方法有种.
-
14、若随机变量服从二项分布 , , 则.
-
15、我们把称为双曲余弦函数,其函数表达式为 , 相应地双曲正弦函数的函数表达式为.若直线与双曲余弦函数曲线和双曲正弦函数曲线分别相交于点A,B,曲线在点A处的切线与曲线在点B处的切线相交于点P,则( )A、是奇函数 B、 C、在区间上随m的增大而减小,在区间上随m的增大而增大 D、的面积为定值
-
16、已知是抛物线:的焦点,过点且倾斜角为135°的直线与交于 , 两点,则( )A、 B、 C、 D、以为直径的圆与抛物线C的准线只有1个公共点
-
17、下列说法正确的是( )A、若回归方程为 , 则变量x与y负相关 B、运用最小二乘法求得的经验回归直线方程一定经过样本点的中心 C、若散点图中所有点都在直线上,则相关系数 D、若决定系数的值越接近于1,表示回归模型的拟合效果越好
-
18、对 , 设是关于x的方程的实数根,数列满足其中符号表示不超过的最大整数,则( )A、1013 B、1015 C、2025 D、2027
-
19、已知正方体的棱长为4,点为的中点,若点 , A,C,都在球O的表面上,则球O的表面积为( )A、11π B、12π C、36π D、44π
-
20、已知双曲线:的焦距为10,左、右焦点分别为 , , 过点作斜率不为0的直线与双曲线的左、右支分别交于 , 两点.若的内切圆与直线相切于点H,且 , 则双曲线的渐近线方程为( ).A、 B、 C、 D、