相关试卷
-
1、已知二次函数 .(1)、若 , 求的解集;(2)、若方程在上有解,求实数a的取值范围.
-
2、2025年是“全民体重管理年”,健康体重成为社会关注的新焦点.为了提升人们体重管理意识和技能,预防控制超重肥胖,某市开展“体重管理知识”宣传活动.举办了“体重管理”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(成绩均为不低于40分的整数)进行适当分组后(每组为左闭右开的区间),得到如图所示的频率分布直方图.
 (1)、求图中a的值与该样本数据的第60百分位数;(2)、根据该频率分布直方图,估计1000个参赛选手中有多少人能得60分及以上.
(1)、求图中a的值与该样本数据的第60百分位数;(2)、根据该频率分布直方图,估计1000个参赛选手中有多少人能得60分及以上. -
3、已知函数在上恰有2个零点,则a的取值范围是 .
-
4、已知甲,乙两个投篮命中率分别是 , 并且他们投篮互不影响,每人投篮1次,则恰好有一个人命中的概率为 .
-
5、计算: .
-
6、若球的半径为2,为直径,中点为P,则下列说法正确的是( )A、球面上任意一点到P距离的最大值为3 B、过P作球O的截面,则截面面积的最小值是 C、若某正方体的外接球是球O,则点P到该正方体各面距离的最大值是 D、若某正四面体的外接球是球O,则点P在该正四面体上的轨迹长度是
-
7、已知点 , 则以下说法正确的是( )A、 B、 C、 D、在上的投影向量是
-
8、如图,已知正方体的棱长为1,点P是上底面内的一个动点.设平面与平面的夹角为 , 平面与平面的夹角为 , 若 , 则下图中阴影部分表示P点轨迹的是( )
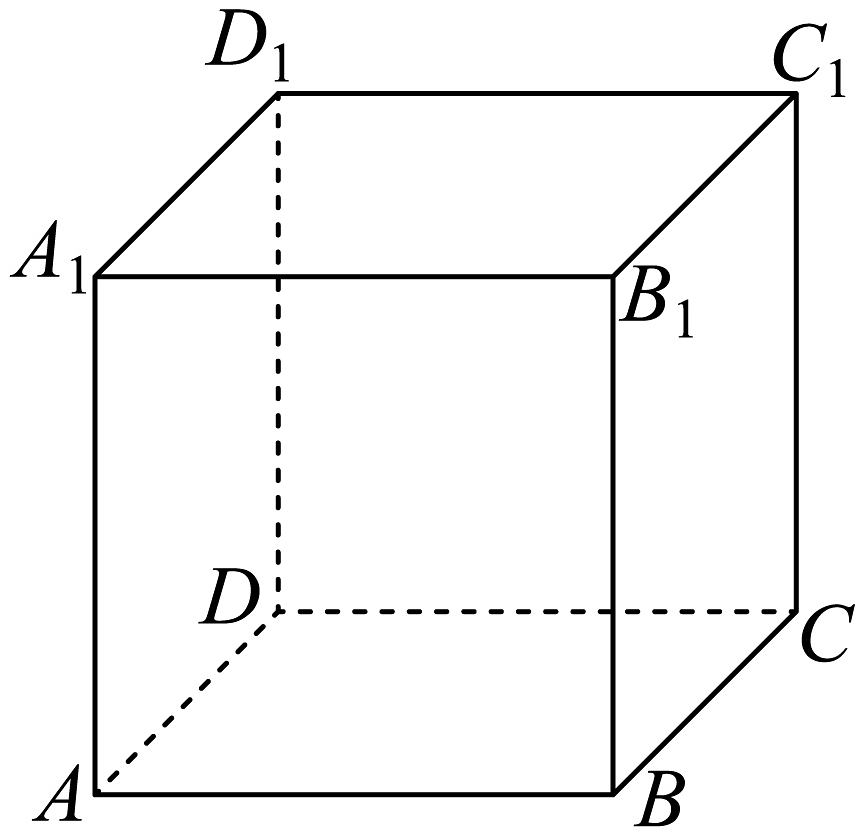 A、
A、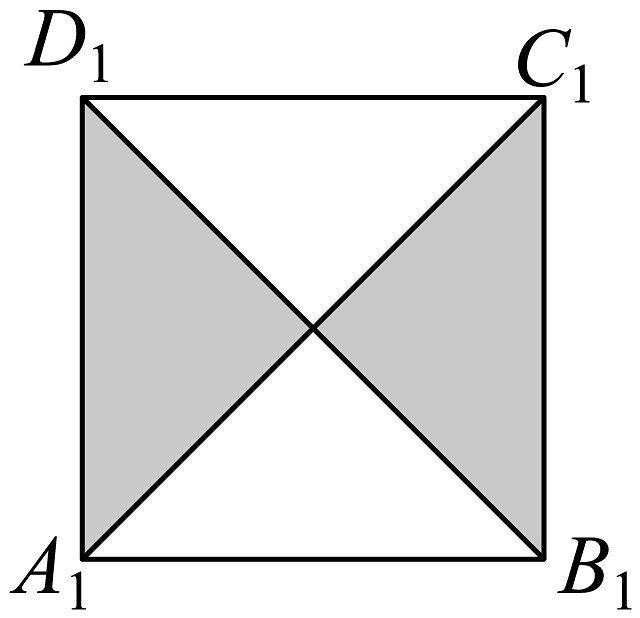 B、
B、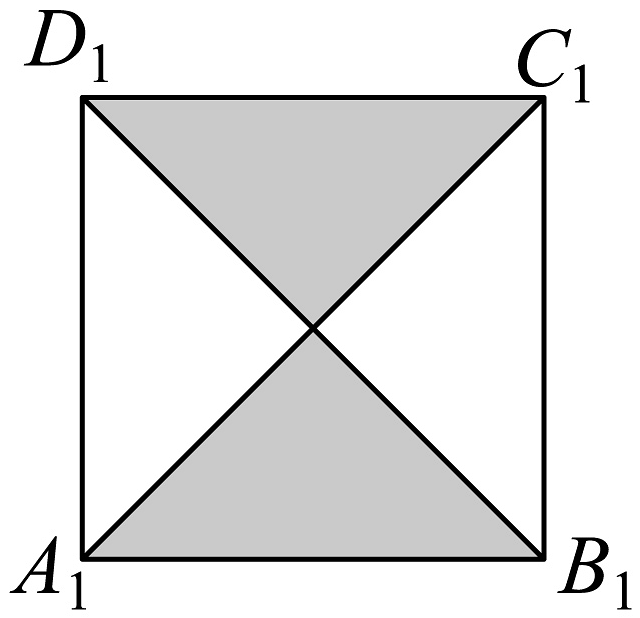 C、
C、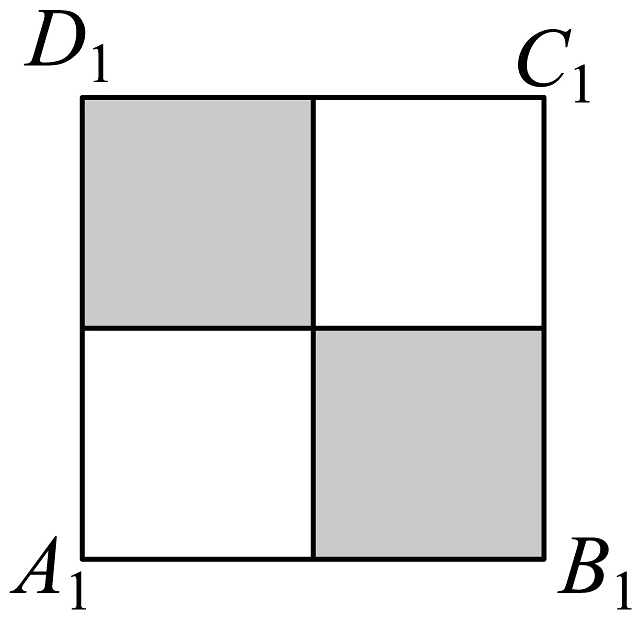 D、
D、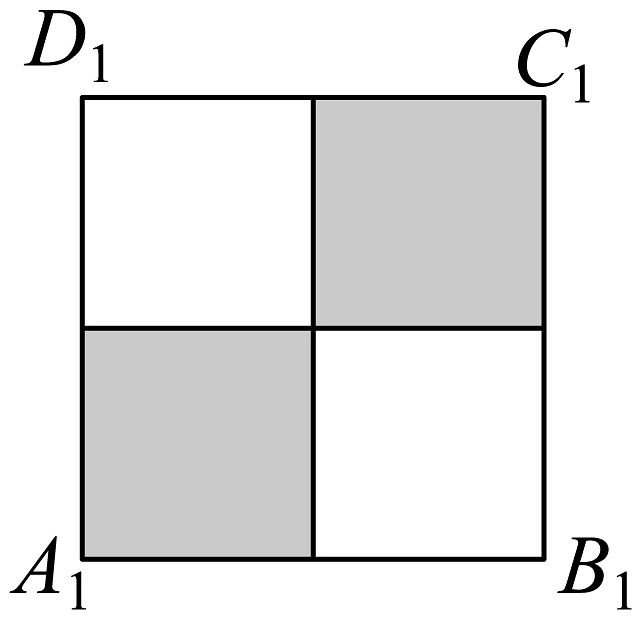
-
9、如图是某函数的部分图象,则该函数最有可能的解析式是( )
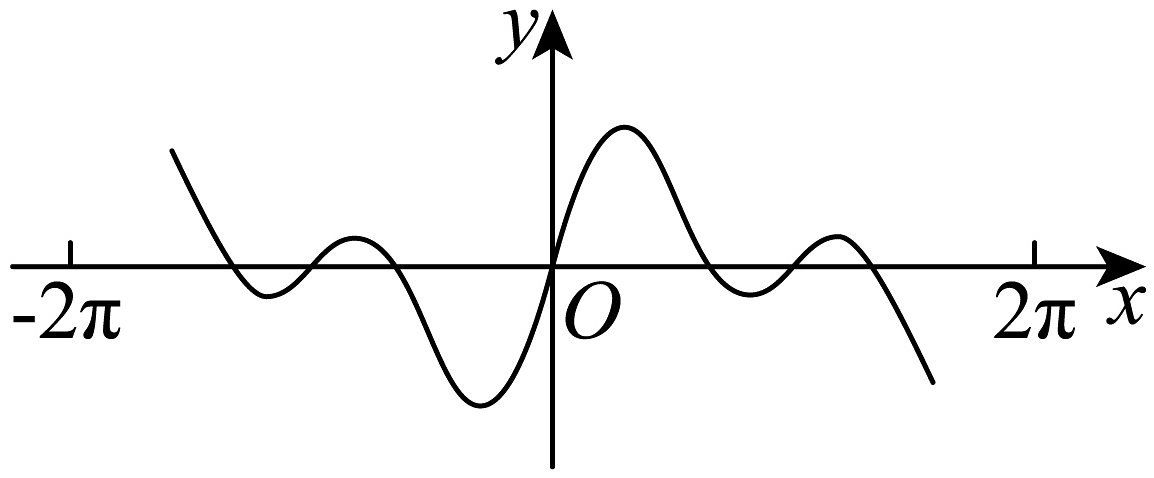 A、 B、 C、 D、
A、 B、 C、 D、 -
10、以下说法正确的是( )A、 B、 C、 D、
-
11、设样本空间含有等可能的样本点,且 , 则( )A、 B、 C、 D、
-
12、某次测量中得到的样本数据如下:82,84,84,86,86,86,88,88,88,88.若样本数据恰好是样本数据都加2后所得,则两样本的下列数字特征对应相同的是( )A、众数 B、平均数 C、中位数 D、方差
-
13、已知复数 , 则z在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
14、设集合 , 则( )A、 B、 C、 D、
-
15、若函数满足:对 , 都有 , 则称该函数具有性质 , 下列函数具有性质的是( )A、 B、 C、 D、
-
16、已知函数是偶函数.(1)、求的值;(2)、若 , , , 不等式对任意恒成立,求的取值范围.
-
17、如图,四棱锥的底面是菱形,且平面 , E,F分别是棱PB,PC的中点.
 (1)、求证:平面PAD.(2)、求证:平面平面PAC.(3)、若 , 求直线DF和平面PAB所成角的正弦值.
(1)、求证:平面PAD.(2)、求证:平面平面PAC.(3)、若 , 求直线DF和平面PAB所成角的正弦值. -
18、中国新能源汽车产业发展势头迅猛,社会关注度持续增长.大数据显示,不同品牌的新能源汽车,其关注群体有不同的年龄分布.某网站面向关注新能源汽车的站内用户群体做了一个问卷调查,从关注品牌A的网友中随机抽取300人,并将他们按年龄分成了 , , , , (单位:岁)这五组,并画出频率分布直方图如图所示.
 (1)、求图中a的值和80%分位数(精确到小数点后一位);(2)、根据以上数据,估计该网站用户中关注新能源品牌A的网友的平均年龄.
(1)、求图中a的值和80%分位数(精确到小数点后一位);(2)、根据以上数据,估计该网站用户中关注新能源品牌A的网友的平均年龄. -
19、已知正实数x,y满足 , 则的取值范围.
-
20、已知正三角形ABC边长为12,点E为AB边的中点, , 若点P是边上的动点,则满足的点P有个