相关试卷
-
1、如图,八面体的每一个面都是边长为4的正三角形,且顶点B,C,D,E,在同一个平面内.若点在四边形内(包含边界)运动,当时,则点的轨迹的长度为 .
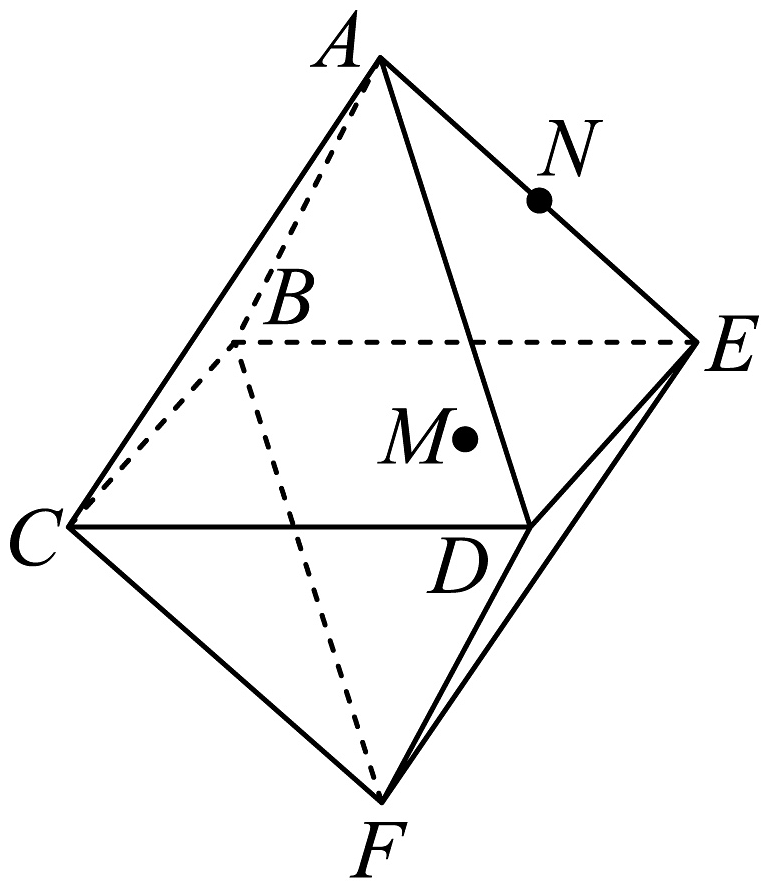
-
2、当时,的解集为 .
-
3、使成立的一个充分而非必要的条件是 .
-
4、著名数学家狄利克雷在数学领域成就显著,以其命名的函数 , 被称为狄利克雷函数,其中为实数集,为有理数集,下面关于狄利克雷函数的正确结论是( )A、对于任意的 , 都有 B、函数是偶函数 C、若且为有理数,则对任意的恒成立 D、在图象上存在不同的三个点 , 使得为直角三角形
-
5、假设某人在出生起180天内的体力、情绪、智力呈周期性变化,它们的变化规律遵循如图所示的正弦型曲线模型:
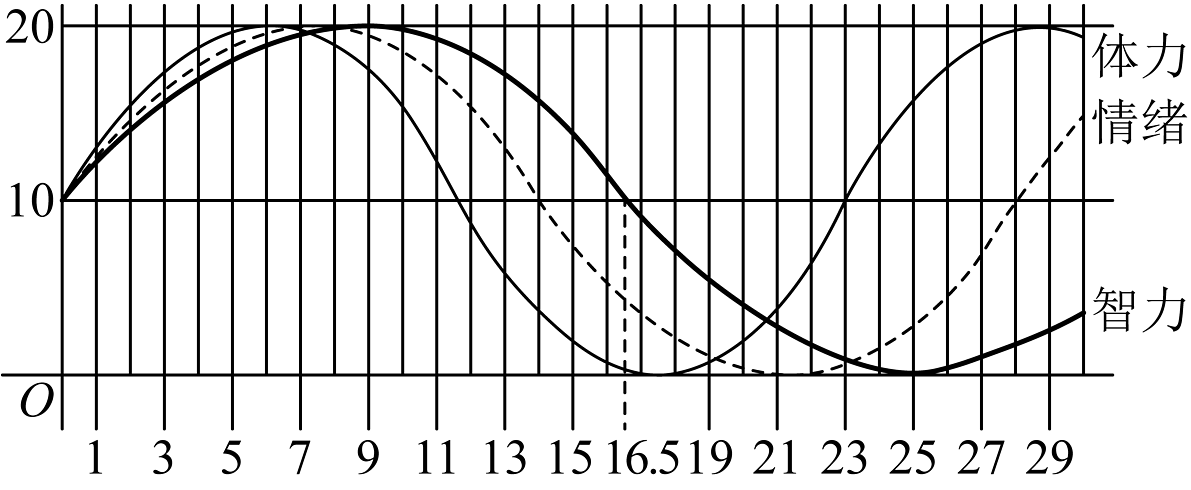
记智力曲线为 , 情绪曲线为 , 体力曲线为 , 且三条曲线的起点位于坐标系的同一点处、均为可向右延伸,则( )
A、智力曲线的最小正周期是三个曲线中最大的 B、在出生起180天内,体力共有7次达高峰值 C、第94天时,情绪值小于15 D、第62天时,智力曲线和情绪曲线均处于上升期 -
6、对于一个古典概型的样本空间和事件A,B,C,D,用表示事件中的样本点个数.若 , , , , , , , , 则( )A、与对立 B、与不对立 C、与互斥 D、与相互独立
-
7、已知函数 , 若 , 则的取值范围是( )A、 B、 C、 D、
-
8、已知向量 , , 若 , 则实数( )A、3 B、6 C、 D、
-
9、已知一组数据39,41,44,46,49,50,x,55的第65百分位数是50,那么实数的取值范围是( )A、 B、 C、 D、
-
10、已知 , , 则( )A、 B、 C、 D、或
-
11、如图,圆台的侧面展开图扇环的圆心角为 , 其中 , 则该圆台的高为( )
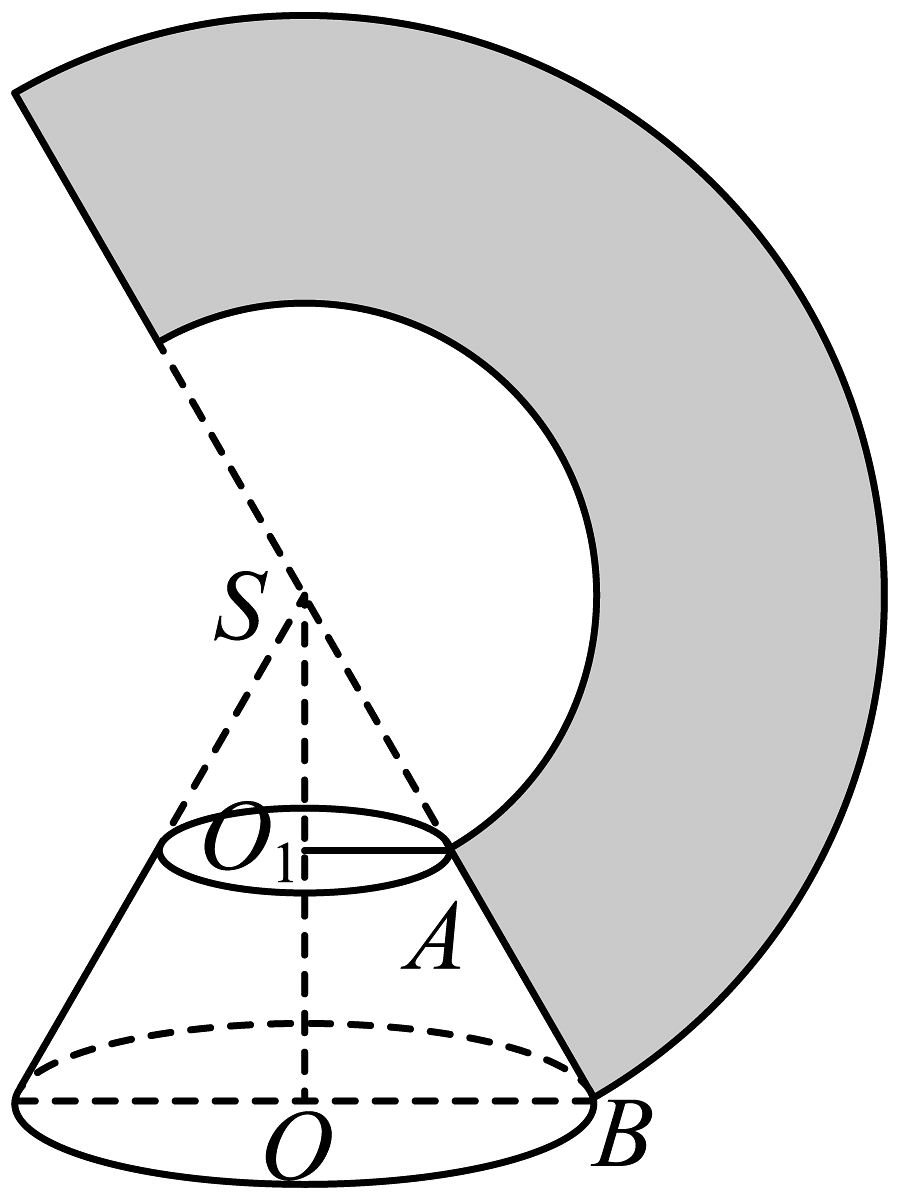 A、 B、 C、1 D、4
A、 B、 C、1 D、4 -
12、已知复数 , , 在复平面内,复数和所对应的两点之间的距离是( )A、 B、10 C、 D、5
-
13、设集合 , , 则集合的元素个数为A、4 B、3 C、2 D、1
-
14、已知.(1)、求点到直线的距离;(2)、求的外接圆的方程.
-
15、已知直线过点 , 且在轴上的截距为在轴上的截距的两倍,则直线的方程是.
-
16、下列说法正确的有( )A、若直线经过第一、二、四象限,则在第二象限 B、任何一条直线都有倾斜角,都存在斜率 C、方程能表示平行轴的直线 D、直线的斜率越大,倾斜角越大
-
17、某商家为吸引顾客,准备了两份奖品,凡是进店消费即可参与抽奖,奖品被抽完即抽奖活动终止.抽奖的规则如下:在一个不透明的盒子中有放回地取球(小球大小和质地相同),取出红球,则不获奖,取出白球,则获奖.刚开始盒子中有个白球和个红球,参与抽奖的顾客从盒子中随机抽取1个球,若不获奖,则将球放回,该顾客抽奖结束,下一名顾客继续抽奖.若获奖,则将球放回后再往盒子中加个红球,该顾客再继续抽奖.若第二次抽奖不获奖,则将球放回,该顾客只获得一份奖品,抽奖结束,下一名顾客继续抽奖;若第二次抽奖获奖,则该顾客获得两份奖品,整个抽奖活动结束.该活动深受顾客喜欢,假设这两份奖品没被抽完前始终有顾客参与抽奖.(1)、求第名和第名顾客各抽中一份奖品的概率;(2)、求这两份奖品都被第名顾客抽取的概率;(3)、求由第名顾客终止抽奖活动的概率.
-
18、(1)过的重心G作直线l,若l与边平行,与分别交于D,E两点,求与的面积比;
(2)在中,若 , 其中 , 过O作直线l,与线段分别交于D,E两点,求证:;
(3)在等腰直角中, , 分别为的中点,将沿折起,得到四棱锥 , 在二面角处于过程中,作的角平分线交于点M,记与平面的交点为N,过N作直线l,与线段分别交于P,Q两点,记四棱锥的体积为 , 四棱锥的体积为V,求的最小值.
-
19、如图,在中, , 是的角平分线,且 .
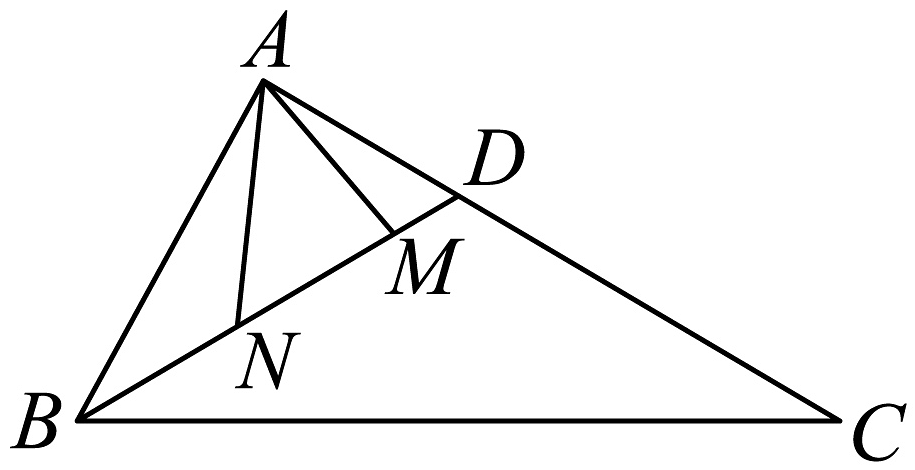 (1)、求;(2)、若是线段上动点,且 , 记为 .
(1)、求;(2)、若是线段上动点,且 , 记为 .(i)用表示;
(ii)求面积的最小值.
-
20、在三棱锥中,是的中点,且 .
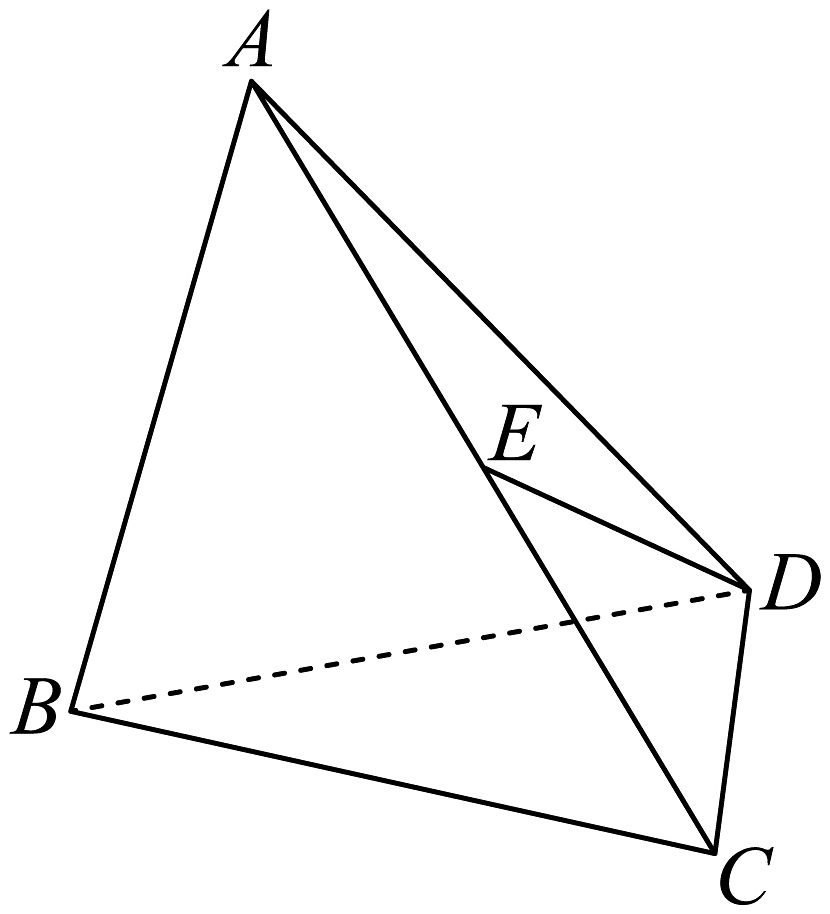 (1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.
(1)、求证:平面平面;(2)、求直线与平面所成角的正弦值.