-
1、已知(1)、当时,求不等式的解集;(2)、若在上为增函数,求的取值范围.
-
2、已知集合 , .(1)、若 , 求 , ;(2)、若 , 求实数的取值范围.
-
3、计算.
-
4、已知的定义域为 , 则的定义域是.
-
5、下列说法正确的是( )A、函数在定义域内是减函数 B、若 , 则函数的最大值为 C、若不等式对一切实数恒成立,则 D、若 , , , 则的最小值为2
-
6、已知集合 , , 则下列选项中正确的是( )A、集合有32个子集 B、 C、中所含元素的个数为10个 D、
-
7、已知幂函数 , 则以下结论正确的是( )A、的定义域为 B、是减函数 C、的值域为 D、是偶函数
-
8、若定义在上的偶函数在上单调递减,且 , 则满足的的取值范围是( )A、 B、 C、 D、
-
9、函数的图象大致为( )A、
 B、
B、 C、
C、 D、
D、
-
10、下列函数中最小值为4的是( )A、 B、 C、 D、
-
11、设函数 , 则( )A、是奇函数,且在上单调递增 B、是奇函数,且在上单调递减 C、是偶函数,且在上单调递增 D、是偶函数,且在上单调递减
-
12、已知集合 , 则的值为( )A、0 B、1 C、 D、1或
-
13、下列说法正确的是( )A、 , B、“且”是“”的充要条件 C、 , D、“”是“”的必要不充分条件
-
14、已知全集 , 集合 , , 则( )A、 B、 C、 D、
-
15、某汽车销售公司为了提升公司的业绩,将最近一段时间内每日的汽车销售情况进行了统计,如图所示.
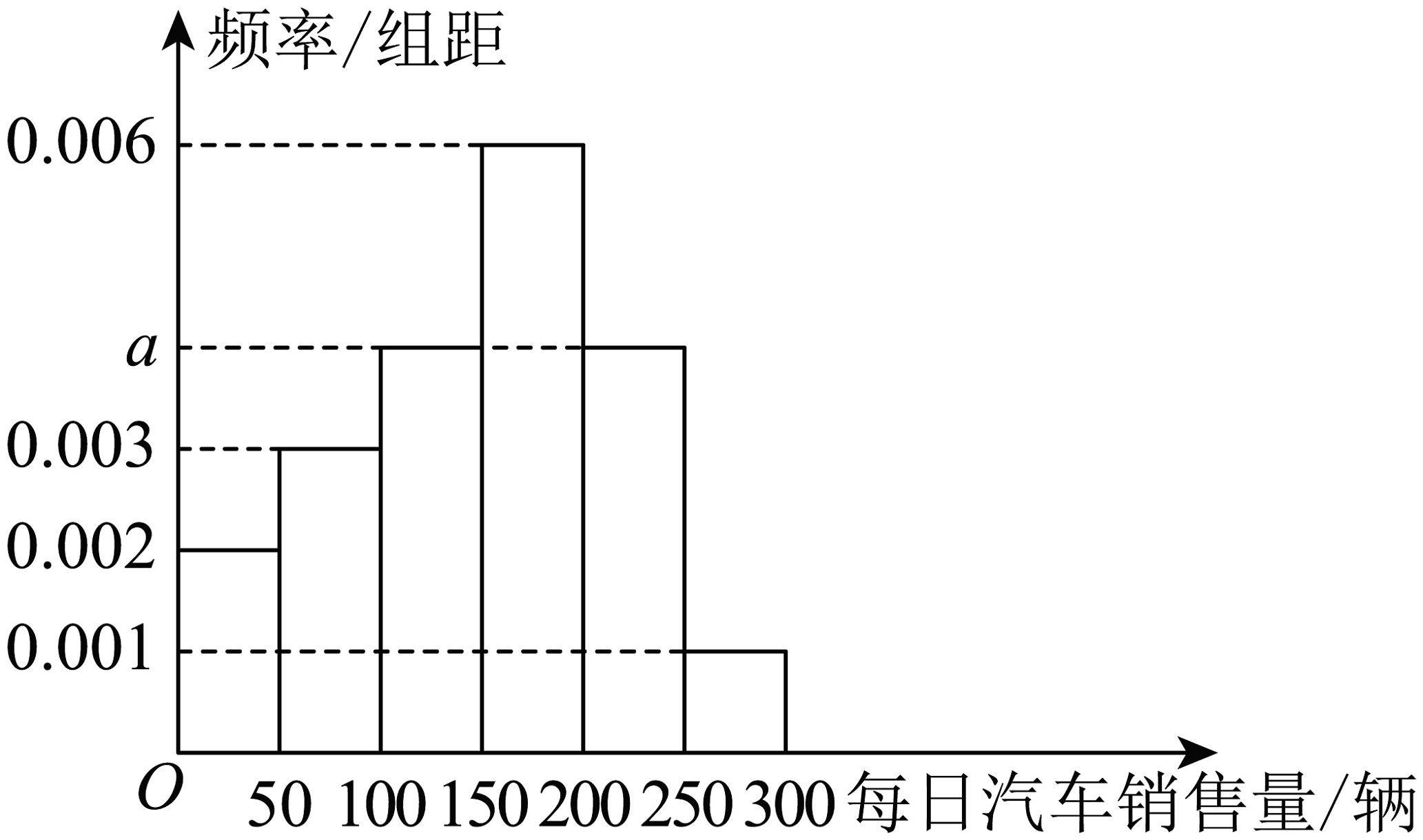 (1)、求的值,并求该公司这段时间内每日汽车销售量的第60百分位数;(2)、以频率估计概率,若在这段时间内随机选择4天,设每日汽车销售量在内的天数为 , 在恰有1天的汽车销售量不超过150辆的条件下,求的分布列及数学期望;(3)、为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥中,、均是边长为2的正三角形, , 现从写有数字1~8的八个标签中随机选择两个分别贴在、两个顶点,记顶点、上的数字分别为和 , 若为侧棱上一个动点,满足 , 当“二面角大于”即为中奖,求中奖的概率.
(1)、求的值,并求该公司这段时间内每日汽车销售量的第60百分位数;(2)、以频率估计概率,若在这段时间内随机选择4天,设每日汽车销售量在内的天数为 , 在恰有1天的汽车销售量不超过150辆的条件下,求的分布列及数学期望;(3)、为增加销售量,公司规定顾客每购买一辆汽车可以进行一次抽奖活动,规则如下:在三棱锥中,、均是边长为2的正三角形, , 现从写有数字1~8的八个标签中随机选择两个分别贴在、两个顶点,记顶点、上的数字分别为和 , 若为侧棱上一个动点,满足 , 当“二面角大于”即为中奖,求中奖的概率. -
16、两个有共同底面的正三棱锥与 , 它们的各顶点均在半径为1的球面上,若二面角的大小为 , 则的边长为 .
-
17、某圆锥母线长为1,其侧面积与轴截面面积的比值为 , 则该圆锥体积为.
-
18、已知函数 , 则下列结论中正确的是( )A、函数有两个零点 B、恒成立 C、若方程有两个不等实根,则的范围是 D、直线与函数图象有两个交点
-
19、在三棱柱中,点在棱上,且 , 点为的中点,点在棱上,若平面 , 则( )A、2 B、3 C、4 D、5
-
20、阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数(且)的点的轨迹是圆,后人将这个圆称为阿氏圆.已知动点到点与点的距离之比为2,记动点的轨迹为曲线.
(1)求曲线的方程;
(2)过点作曲线的切线,求切线方程.