版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、函数 $f (x) = A sin (ω x + φ) (A > 0, ω > 0, |φ| < \frac{π}{2})$ 的部分图象如图所示，则下列结论正确的是（）

A、 $f (x) = sin (2 x + \frac{π}{3})$ B、 $f (x) = sin (2 x - \frac{π}{3})$ C、 $f (x) = sin (x + \frac{π}{3})$ D、 $f (x) = sin (x - \frac{π}{3})$

查看解析
2、已知函数 $f (x)$ 是定义在 $R$ 上的奇函数， $f (x) = f (x + 4)$ ，且 $f (- 1) = - 1$ ，则 $f (2024) + f (2025) =$ （）

A、 $- 1$ B、0 C、1 D、2

查看解析
3、已知曲线 $C_{1} : y = sin x, C_{2} : y = sin (2 x + \frac{π}{3})$ .
①把 $C_{1}$ 向左平移 $\frac{π}{3}$ 个单位长度，再将所有点的横坐标变为原来的2倍，得到 $C_{2}$
②把 $C_{1}$ 向左平移 $\frac{π}{3}$ 个单位长度，再将所有点的横坐标变为原来的 $\frac{1}{2}$ 倍，得到 $C_{2}$
③把 $C_{1}$ 上所有点的横坐标变为原来的 $\frac{1}{2}$ 倍，再向左平移 $\frac{π}{3}$ 个单位长度，得到 $C_{2}$
④把 $C_{1}$ 上所有点的横坐标变为原来的 $\frac{1}{2}$ 倍，再向左平移 $\frac{π}{6}$ 个单位长度，得到 $C_{2}$ ，
上列说法中正确的是（）

A、①③ B、②③ C、①④ D、②④

查看解析
4、已知幂函数的图象经过点 $P (2, \frac{1}{4})$ ，该幂函数的大致图象为（）

A、 B、 C、 D、

查看解析
5、求值： $\frac{tan \frac{π}{12}}{1 - {tan}^{2} \frac{π}{12}} =$ （）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{6}$

查看解析
6、“四边形是菱形”是“四边形是平行四边形”的（）

A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不必要又不充分条件

查看解析
7、命题 $P : \forall x \in (0, \frac{π}{2}), sin x \leq x$ ，则 $\neg p$ 为（）

A、 $\forall x \in (0, \frac{π}{2}), sin x \geq x$ B、 $\forall x \in (0, \frac{π}{2}), sin x > x$ C、 $\exists x \in (0, \frac{π}{2}), sin x \leq x$ D、 $\exists x \in (0, \frac{π}{2}), sin x > x$

查看解析
8、若全集 $U = \{- 4, - 3, - 1, 0, 1, 3, 4\}$ ，集合 $A = \{- 3, - 1, 0, 1\}, B = \{- 4, 0, 1, 3\}$ ，则 $(∁_{U} B) \cap A =$ （）

A、 $\{3, - 1\}$ B、 $\{0, 1\}$ C、 $\{- 3, - 1\}$ D、 $\{- 3, - 1, 4\}$

查看解析
9、若存在常数 $t$ ，使得数列 $\{a_{n}\}$ 满足 $a_{n + 1} - a_{1} a_{2} a_{3} \dots a_{n} = t (n \geq 1, n \in N)$ ，则称数列 $\{a_{n}\}$ 为“ $H (t)$ 数列”．

(1)、判断数列：1，3，5，10，152是否为“ $H (2)$ 数列”，并说明理由；

(2)、若数列 $\{a_{n}\}$ 是首项为2的“ $H (t)$ 数列”，数列 $\{b_{n}\}$ 是等比数列，且 $\{a_{n}\}$ 与 $\{b_{n}\}$ 满足 $\sum_{i = 1}^{n} a_{i}^{2} = a_{1} a_{2} a_{3} \dots a_{n} + \log_{2} b_{n}$ ，求 $t$ 的值和数列 $\{b_{n}\}$ 的通项公式；

(3)、若数列 $\{a_{n}\}$ 是“ $H (t)$ 数列”， $S_{n}$ 为数列 $\{a_{n}\}$ 的前 $n$ 项和， $a_{1} > 1$ ， $t > 0$ ，证明： $t > S_{n + 1} - S_{n} - e^{S_{n} - n}$ ．

查看解析
10、已知复数z满足 $z (1 - i) = {|1 + i|}^{2}$ ，则 $z =$ （）

A、 $1 - i$ B、 $1 + i$ C、 $- 1 - i$ D、 $- 1 + i$

查看解析
11、定义运算： $|\begin{matrix} m & n \\ p & q \end{matrix}| = m q - n p$ ，已知函数 $f (x) = |\begin{matrix} \ln x & x - 1 \\ 1 & a \end{matrix}|$ ， $g (x) = \frac{1}{x} - 1$ ．

(1)、若函数 $f (x)$ 的最大值为0，求实数a的值；

(2)、若函数 $h (x) = f (x) + g (x)$ 存在两个极值点 $x_{1}$ ， $x_{2}$ ，证明： $\frac{h (x_{1}) - h (x_{2})}{x_{1} - x_{2}} - a + 2 < 0$ ；

(3)、证明： $(1 + \frac{1}{2^{2}}) (1 + \frac{1}{3^{2}}) (1 + \frac{1}{4^{2}}) ... (1 + \frac{1}{n^{2}}) < e$ ．

查看解析
12、已知椭圆 $E : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点别为 $F_{1}$ ， $F_{2}$ ，离心率为 $\frac{\sqrt{2}}{2}$ ，过点 $F_{1}$ 的动直线l交E于A，B两点，点A在x轴上方，且l不与x轴垂直， $△ A B F_{2}$ 的周长为 $4 \sqrt{2}$ ，直线 $A F_{2}$ 与E交于另一点C，直线 $B F_{2}$ 与E交于另一点D，点P为椭圆E的下顶点，如图．

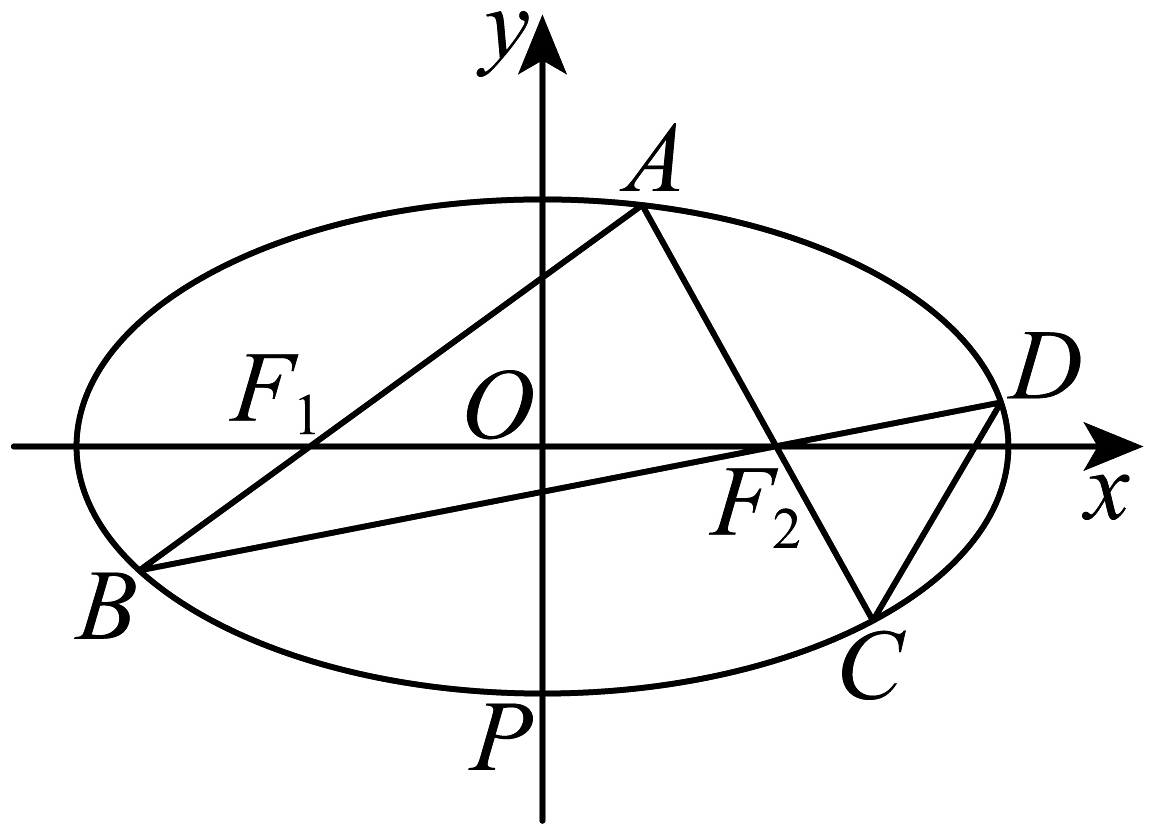(1)、求E的方程；

(2)、证明：直线CD过定点．

查看解析
13、某校为了解本校学生课间进行体育活动的情况，随机抽取了50名男生和50名女生，通过调查得到如下数据：50名女生中有10人课间经常进行体育活动，50名男生中有20人课间经常进行体育活动．

(1)、请补全 $2 \times 2$ 列联表，试根据小概率值 $α = 0.05$ 的独立性检验，判断性别与课间经常进行体育活动是否有关联；
性别
体育活动
合计
课间不经常进行体育活动
课间经常进行体育活动
男
女
合计

(2)、以样本的频率作为概率的值，在全校的男生中任取4人，记其中课间经常进行体育活动的人数为 $X$ ，求 $X$ 的分布列、数学期望和方差．
附表：
$α$
0.1
0.05
0.01
0.005
0.001
$x_{α}$
2.706
3.841
6.635
7.879
10.828
附： $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ ．

查看解析
14、若 ${(2 - x)}^{7} = a_{0} + a_{1} (1 + x) + a_{2} {(1 + x)}^{2} + \dots + a_{7} {(1 + x)}^{7}$ ，则 $a_{0} + a_{1} + a_{2} + \dots + a_{7}$ 的值为．

查看解析
15、我国5G技术研发试验在2016~2018年进行，分为5G关键技术试验、5G技术方案验证和5G系统验证三个阶段.2020年初以来，5G技术在我国已经进入高速发展的阶段，5G手机的销量也逐渐上升．某手机商城统计了2022年5个月5G手机的实际销量，如下表所示：
月份
2022年1月
2022年2月
2022年3月
2022年4月
2022年5月
月份编号x
1
2
3
4
5
销量y（部）
50
96
a
185
227
若y与x线性相关，且求得回归直线方程为 $\hat{y} =$ $45 x + 5$ ，则下列说法正确的是（）

A、 $a = 142$ B、 $y$ 与 $x$ 正相关 C、 $y$ 与 $x$ 的相关系数为负数 D、2022年7月该手机商城的5G手机销量约为365部

查看解析
16、若“ $\exists x \in [4, 6]$ ， $x^{2} - a x - 1 > 0$ ”为假命题，则实数 $a$ 的取值可以为（）

A、8 B、7 C、6 D、5

查看解析
17、双曲线 $C : \frac{x^{2}}{a^{2}} - \frac{y^{2}}{5} = 1 (a > 0)$ 的左､右焦点分别为 $F_{1}, F_{2}$ ，离心率为 $\frac{\sqrt{5}}{2}$ ，右支上一点 $P$ 满足 $P F_{1} ⊥ P F_{2}$ ，直线 $l$ 平分 $∠ F_{1} P F_{2}$ ，过点 $F_{1}, F_{2}$ 作直线 $l$ 的垂线，垂足分别为 $A, B$ .设 $O$ 为坐标原点，则 $△ O A B$ 的面积为（）

A、 $2 \sqrt{5}$ B、 $4 \sqrt{5}$ C、10 D、 $10 \sqrt{2}$

查看解析
18、有 $5$ 个人到南京、镇江、扬州的三所学校去应聘，若每人至多被一个学校录用，每个学校至少录用其中一人，则不同的录用情况种数是（）

A、90 B、150 C、390 D、420

查看解析
19、在空间直角坐标系中， $P (0, 0, 0), A (1, 0, 0), B (0, 2, 0), C (0, 0, 3)$ ，三角形 $A B C$ 重心为 $G$ ，则点 $P$ 到直线 $A G$ 的距离为（）

A、 $\frac{6}{7}$ B、 $\frac{\sqrt{221}}{17}$ C、 $\frac{2 \sqrt{17}}{17}$ D、 $\frac{\sqrt{5}}{3}$

查看解析
20、设 $a = \frac{1}{2} \cos 6 ° - \frac{\sqrt{3}}{2} \sin 6 °$ ， $b = 2 \sin 13 ° \cos 13 °$ ， $c = \sqrt{\frac{1 - \cos 50^{°}}{2}}$ ，则有（）

A、 $c < b < a$ B、 $a < b < c$ C、 $a < c < b$ D、 $b < c < a$

查看解析

上一页 973 974 975 976 977 下一页跳转

性别	体育活动		合计
性别	课间不经常进行体育活动	课间经常进行体育活动
男
女
合计

月份	2022年1月	2022年2月	2022年3月	2022年4月	2022年5月
月份编号x	1	2	3	4	5
销量y（部）	50	96	a	185	227

$α$	0.1	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828