版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、已知椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{a^{2} - 6} = 1$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，则椭圆 $C$ 的长轴长为（）

A、 $2 \sqrt{3}$ B、 $4 \sqrt{2}$ C、 $4 \sqrt{3}$ D、 $6 \sqrt{2}$

查看解析
2、我国著名数学家华罗庚曾说：“数缺形时少直观，形缺数时难入微，数形结合百般好，隔裂分家万事休．”在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来研究函数图象的特征．我们从这个商标中抽象出一个图象如图，其对应的函数可能是（）

A、 $f (x) = \frac{1}{|x - 1|}$ B、 $f (x) = \frac{1}{||x| - 1|}$ C、 $f (x) = \frac{1}{x^{2} - 1}$ D、 $f (x) = \frac{1}{x^{2} + 1}$

查看解析
3、

(1)、已知 $x > 1$ ，求函数 $y = \frac{4}{x - 1} + x$ 的最小值；

(2)、已知正数 $x, y$ 满足 $4 x + y = 1$ ，求 $\frac{1}{x} + \frac{1}{y}$ 的最小值.

查看解析
4、如图，在四棱锥 $P - A B C D$ ， $P A ⊥$ 平面 $A B C D$ ，底面 $A B C D$ 是直角梯形，其中 $A D / / B C$ ， $A B ⊥ A D$ ， $P A = 4, A B = A D = \frac{1}{2} B C = 2,$ ， E为棱 $B C$ 上的点，且 $B E = \frac{1}{4} B C$ .

(1)、求证： $D E ⊥$ 平面 $A P C$ ；

(2)、求平面 $A P C$ 与平面 $P C D$ 所成夹角的正弦值.

查看解析
5、若直线l的方向向量是 $\vec{e} = (- 1, \sqrt{3}) ，$ 则直线l的倾斜角是（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看解析
6、已知 $a = 2023^{2025}$ ， $b = 2024^{2024}$ ， $c = 2025^{2023}$ ，则（）

A、 $a > c > b$ B、 $b > c > a$ C、 $a > b > c$ D、 $c > a > b$

查看解析
7、已知曲线C的方程为： $\{\begin{array}{l} \frac{x^{2}}{4} + \frac{y^{2}}{3} = 1 (y \geq 0) \\ x^{2} + y^{2} = 4 (y < 0) \end{array}$ ， $M (- 1, 0)$ ， $N (1, 0)$ ，过M的直线交曲线C于A、B两点（A在B的上方），已知 $∠ A M N = α$ ， $∠ A N M = β$ ，下列命题正确的是（）

A、 $\sin α + \sin β = 2 \sin (α + β)$ B、 $\tan \frac{α}{2} + 3 \tan \frac{β}{2}$ 的最小值是2 C、 $△ A B N$ 周长的最大值是 $4 + 2 \sqrt{5}$ D、若 $α = \frac{π}{3}$ ，将 $△ A M N$ 沿 $M N$ 翻折，使面 $A M N ⊥$ 面 $M N B$ ，则折后 $|A B| = \frac{3 + \sqrt{13}}{2}$

查看解析
8、下列说法中正确的是（）

A、数据1，2，2，3，4，5的极差与众数之和为7 B、若随机变量X服从二项分布 $X ~ B (20, p)$ ，且 $E (X) = 8$ ，则 $D (X) = 4.8$ C、X和Y是分类变量，若 $χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ 值越大，则判断“X与Y独立”的把握性越大 D、若随机变量X服从正态分布 $X ~ N (2, σ^{2})$ ，且 $P (X > 5) = 0.2$ ，则 $P (- 1 < X < 5) = 0.6$

查看解析
9、已知函数 $f (x) = (a - 2) x^{2} + b x - a + 1$ （a， $b \in R$ 且 $a \neq 2$ ）在区间 $[1, 2]$ 上有零点，则 $a^{2} + b^{2}$ 的最小值为（）

A、 $\frac{3}{2}$ B、 $\frac{1}{2}$ C、2 D、1

查看解析
10、函数 $y = \sin (2 ω x + φ) (ω > 0)$ 的部分图象如图所示，直线 $y = \frac{1}{2}$ 与其交于A，B两点，若 $|A B| = \frac{π}{3}$ ，则 $ω =$ （）

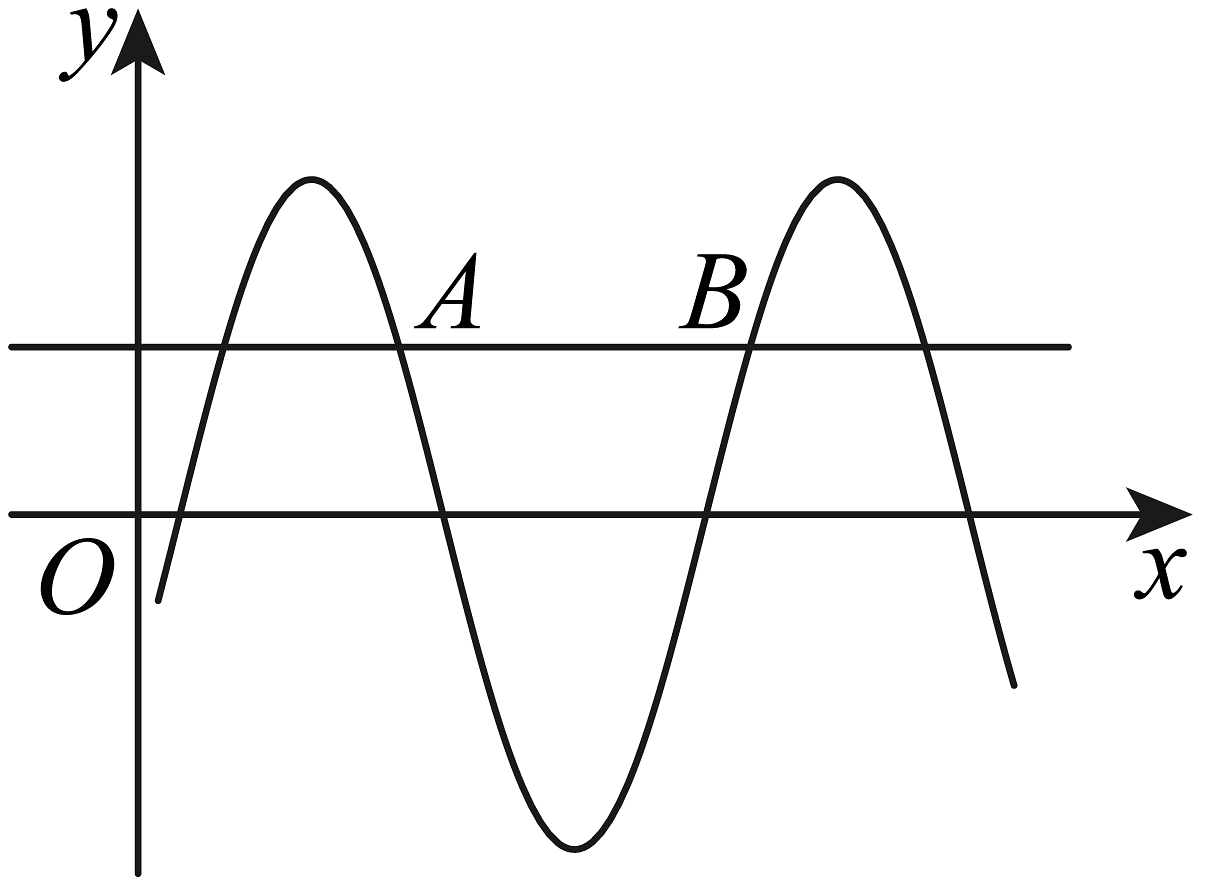A、4 B、3 C、2 D、1

查看解析
11、在 $△ A B C$ 中，D是BC上一点，满足 $\vec{B D} = 2 \vec{D C}$ ， M是AD的中点，若 $\vec{B M} = λ \vec{B A} + μ \vec{B C}$ ，则 $λ + μ =$ （）

A、 $\frac{5}{4}$ B、 $\frac{7}{8}$ C、 $\frac{5}{6}$ D、 $\frac{5}{8}$

查看解析
12、若命题“ $\exists x \in R$ ， $x^{2} + 2 x + a < 0$ 成立”是真命题，则实数a的取值范围是（）

A、 $a \leq 1$ B、 $a < 1$ C、 $a \geq 1$ D、 $a > 1$

查看解析
13、设复数 $z_{1}$ ， $z_{2}$ 在复平面内对应的点关于实轴对称， $z_{1} = 2 - i$ ，则 $\frac{z_{1}}{z_{2}} =$ （）

A、 $\frac{3}{5} - \frac{4}{5} i$ B、 $\frac{3}{5} + \frac{4}{5} i$ C、 $1 + \frac{4}{5} i$ D、 $1 - \frac{4}{5} i$

查看解析
14、已知集合 $A = \{0, - 1\}$ ， $B = \{0, 1, 2 - a\}$ 且 $A \subseteq B$ ，则a等于（）

A、1 B、 $- 1$ C、 $- 3$ D、3

查看解析
15、已知方程 $\frac{x^{2}}{7 - t} + \frac{y^{2}}{t - 1} = 1$ 表示的曲线为C，则下列四个结论中正确的是（）

A、当 $1 < t < 7$ 时，曲线C是椭圆 B、当 $t > 7$ 或 $t < 1$ 时，曲线C是双曲线 C、若曲线C是焦点在x轴上的椭圆，则 $4 < t < 7$ D、若曲线C是焦点在y轴上的双曲线，则 $t > 7$

查看解析
16、已知 $A$ 、 $B$ 是椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 长轴的两顶点， $M$ 是椭圆上的一点，直线 $A M$ 与 $B M$ 斜率之积 $k_{A M} \cdot k_{B M} > - \frac{1}{4}$ ，则此椭圆的离心率取值范围是（）

A、 $(\frac{1}{4}, 1)$ B、 $(\frac{1}{2}, 1)$ C、 $(\frac{\sqrt{2}}{2}, 1)$ D、 $(\frac{\sqrt{3}}{2}, 1)$

查看解析
17、已知抛物线 $C : y^{2} = 2 p x (p > 0)$ 的焦点F在直线 $l : y = x - 1$ 上．

(1)、求C的方程；

(2)、过点 $P (0, - 1)$ 的直线交C于M，N两点，又点Q在线段MN上，且 $\frac{|P M|}{|P N|} = \frac{|Q M|}{|Q N|}$ ，证明：点Q在定直线上．

查看解析
18、在四棱锥 $P - A B C D$ 中，底面ABCD是边长为2的正方形，且 $P A = A B$ ， $P A ⊥$ 底面ABCD，点E满足 $2 \vec{P E} = \vec{P C}$ ．

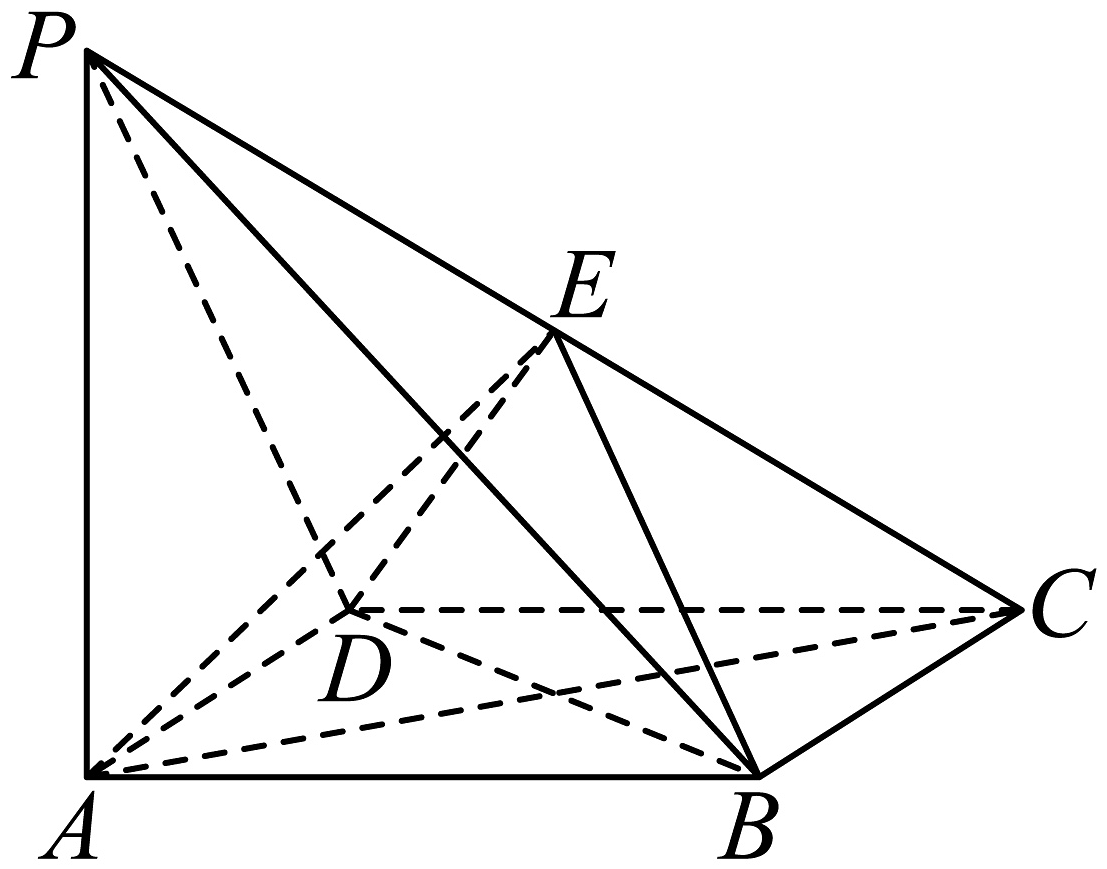(1)、证明： $B D ⊥$ 平面PAC；

(2)、求平面ABE与平面BDE的夹角的大小．

查看解析
19、2024年5月底，各省教育厅陆续召开了2024年高中数学联赛的相关工作，某市经过初次选拔后有小明，小王，小红三名同学成功进入决赛，在决赛环节中三名同学同时解答一道有关组合数论的试题．已知小明成功解出这道题的概率是 $\frac{3}{4}$ ，小明，小红两名同学都解答错误的概率是 $\frac{1}{12}$ ，小王、小红两名同学都成功解出的概率是 $\frac{1}{4}$ ，这三名同学解答是否正确相互独立.

(1)、分别求出小王，小红两名同学成功解出这道题的概率；

(2)、求三人中至少有两人成功解出这道题的概率．

查看解析
20、已知函数 $f (x) = (x + 1) \ln x$ ，记 $f^{'} (x)$ 为 $f (x)$ 的导函数．

(1)、求曲线 $f (x)$ 在点 $(1, f (1))$ 处的切线方程；

(2)、求 $f^{'} (x)$ 的最值．

查看解析

上一页 965 966 967 968 969 下一页跳转