相关试卷
-
1、已知圆 , 点是直线上的点,则( )A、圆上有两个点到直线的距离为2 B、圆上只有一个点到直线的距离为2 C、从点向圆引切线,切线长的最小值为 D、从点向圆引切线,切线长的最小值是
-
2、已知复数 , 则( )A、的虚部为31i B、 C、为纯虚数 D、
-
3、已知复数z满足 , 为z的共轭复数,则的最大值为( )A、7 B、9 C、25 D、49
-
4、掷两枚质地均匀的正方体骰子,记事件“第一枚骰子向上的点数为偶数”,事件“第二枚骰子向上的点数为奇数”,则( )A、与互为对立事件 B、与互斥 C、 D、
-
5、抛物线的焦点坐标为( )A、 B、 C、 D、
-
6、甲、乙两人独立地攻克一道难题,已知两人能攻克的概率分别是 , , 则该题被攻克的概率为( )A、 B、 C、 D、
-
7、设 , 则z在复平面内所对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
8、函数的零点所在的区间可能是( )A、 B、 , C、 , D、 ,
-
9、已知点是双曲线上任意一点.(1)、求证:点P到双曲线C的两条渐近线的距离的乘积是一个常数;(2)、已知点 , 求的最小值.
-
10、如图,矩形是圆柱的轴截面,分别是上、下底面圆周上的点,且 .
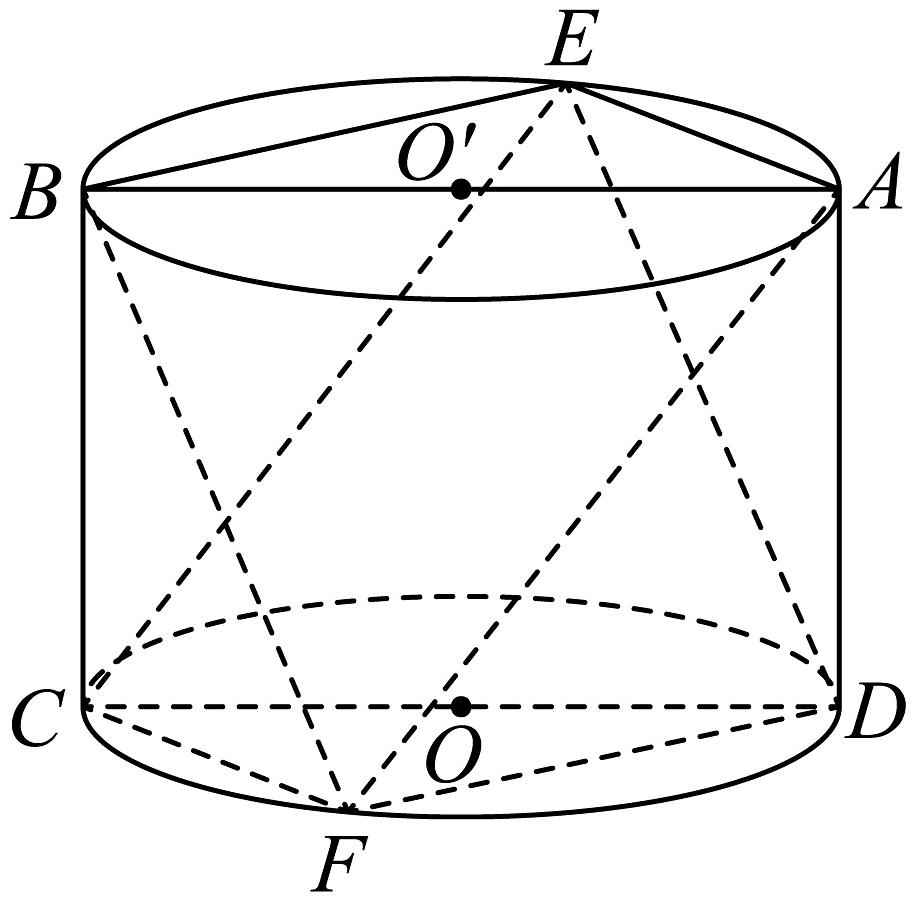 (1)、求证:;(2)、若四边形为正方形,求平面与平面夹角的正弦值
(1)、求证:;(2)、若四边形为正方形,求平面与平面夹角的正弦值 -
11、已知分别是椭圆的右顶点,上顶点和右焦点,若过三点的圆恰与轴相切,则的离心率为 .
-
12、在梯形中, , 则( )A、 B、 C、 D、
-
13、若是方程的实数解,则称是函数与的“复合稳定点”.若函数且与有且仅有两个不同的“复合稳定点”,则的取值范围为( )A、 B、 C、 D、
-
14、造型
 可以看作图中曲线C的一部分,已知C过坐标原点O,且C上的点满足横坐标大于 , 到点的距离与到定直线的距离之积为
可以看作图中曲线C的一部分,已知C过坐标原点O,且C上的点满足横坐标大于 , 到点的距离与到定直线的距离之积为 (1)、求a的值;(2)、当点在C上时,求证:(3)、如图,过点F作两条互相垂直的弦,分别交曲线C于 , , , , 其中 , 求四边形面积的最小值.
(1)、求a的值;(2)、当点在C上时,求证:(3)、如图,过点F作两条互相垂直的弦,分别交曲线C于 , , , , 其中 , 求四边形面积的最小值. -
15、已知为等差数列, , , 记.(1)、求数列 , 的通项公式;(2)、在与之间插入n个数,使这个数组成一个公差为的等差数列,
(i)求数列的前n项和
(ii)在数列中是否存在3项 , , 其中m,k,p成等差数列成等比数列?若存在,求出这样的3项;若不存在,请说明理由.
-
16、已知双曲线的渐近线方程为 , 点在双曲线C上.(1)、求C的方程;(2)、过点的直线l交双曲线C的左支于A,B两点,记直线PA,PB的斜率分别为 , , 是否存在常数 , 使得恒成立?若存在,求的值;若不存在,请说明理由.
-
17、如图,在直三棱柱中, , , , E为的中点,点F满足 , 其中
 (1)、若平面 , 求的值;(2)、当时,求平面与平面夹角的余弦值.
(1)、若平面 , 求的值;(2)、当时,求平面与平面夹角的余弦值. -
18、在平面直角坐标系中,圆经过点 , 且与圆相切于点(1)、求直线的方程;(2)、求圆的标准方程.
-
19、已知抛物线 , 点在C上,k为常数,按照如下方式依次构造点和过点作斜率为k的直线与C的另一交点为 , 过点作斜率为的直线与C的另一交点为 , 记的坐标为 , 的坐标为 , 直线的斜率为 , 则.
-
20、任取一个正整数,若是奇数,就将该数乘3再加上若是偶数,就将该数除以反复进行上述两种运算,经过有限次步骤后,必进入循环圈这就是数学史上著名的“冰雹猜想”又称“角谷猜想”等如取正整数 , 根据上述运算法则得出 , 共需经过3个步骤变成简称为3步“雹程”现给出冰雹猜想的递推关系如下:已知数列满足:为正整数 , , 当时,使得需要步雹程.