相关试卷
-
1、已知点是离心率为的椭圆:上的一点.(1)、求椭圆的方程;(2)、点在椭圆上,点关于坐标原点的对称点为 , 直线和的斜率都存在且不为 , 试问直线和的斜率之积是否为定值?若是,求此定值;若不是,请说明理由;(3)、斜率为的直线交椭圆于、两点,求面积的最大值,并求此时直线的方程.
-
2、如图,在四棱锥中,平面 , 底面是直角梯形,其中 , , , , 为棱上的点,且 , 点在棱上(不与点 , 重合).
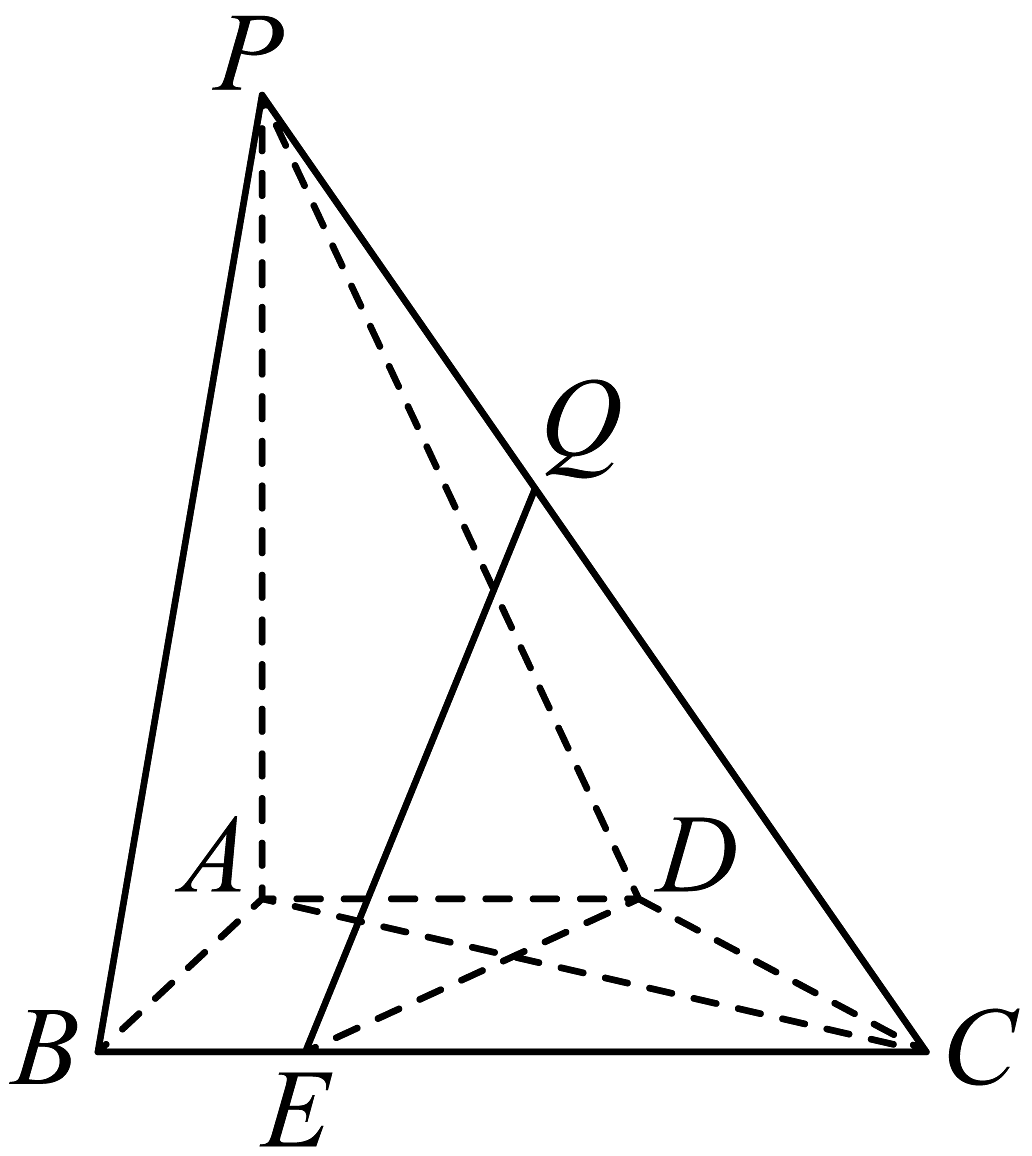 (1)、求证:平面平面;(2)、求二面角的平面角的余弦值;(3)、直线能与平面垂直吗?若能,求出的值;若不能,请说明理由.
(1)、求证:平面平面;(2)、求二面角的平面角的余弦值;(3)、直线能与平面垂直吗?若能,求出的值;若不能,请说明理由. -
3、设平面内两个非零向量的夹角为 , 定义一种运算“”: . 试求解下列问题:(1)、已知向量满足 , 求的值;(2)、①若 , 用坐标表示;
②在平面直角坐标系中,已知点 , 求的值;
(3)、已知向量 , 求的最小值. -
4、如图,某公园有一块扇形人工湖OMN,其中圆心角 , 半径为1千米,为了增加观赏性,公园在人工湖中划分出一片荷花池,荷花池的形状为矩形(四个顶点都落在扇形边界上);再建造一个观景台,形状为 , 记
 (1)、当角取何值时,荷花池的面积最大?并求出最大面积.(2)、若在OA的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元不计桥的宽度;且建造观景台的费用为每平方千米16万元,求建造总费用的范围.
(1)、当角取何值时,荷花池的面积最大?并求出最大面积.(2)、若在OA的位置架起一座观景桥,已知建造观景桥的费用为每千米8万元不计桥的宽度;且建造观景台的费用为每平方千米16万元,求建造总费用的范围. -
5、已知在中, , , 且 .(1)、求的值;(2)、求的长度.
-
6、已知向量 , .(1)、若 , 求;(2)、若向量 , , 求与夹角的余弦值.
-
7、若平面向量 , , 满足 , , , , 则的最小值为 .
-
8、关于平面向量有下列四个命题:
①若 , 则;
②已知 , .若 , 则.
③非零向量和 , 满足 , 则与的夹角为30°.
④.
其中正确的命题为.
-
9、已知是第一象限角,且 , 则.
-
10、摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为60米,转盘直径为50米,设置有24个座舱,摩天轮开启前,距地面最近的点为0号座舱,距地面最远的座舱为12号,座舱逆时针排列且均匀分布,游客甲坐2号舱位,乙坐6号舱位,开启后按逆时针方向匀速旋转,开启后的第8分钟这一时刻,游客甲和乙首次距离地面高度相同,游客甲在摩天轮转动过程中距离地面的高度为米,下列说法正确的是( )A、关于的函数解析式为 B、开启后第20分钟这一时刻游客甲和乙第二次距离地面高度相同 C、开启后第10分钟游客乙距离地面47.5米 D、开启后第10分钟至第18分钟游客甲和乙运动方向相同(上升或下降)
-
11、已知向量 , , 满足 , , , 则( )A、 B、当时, C、当时, D、在上的投影向量的坐标为
-
12、我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明,后人称其为“赵爽弦图”,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图所示.在“赵爽弦图”中,若 , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、互相垂直且有公共原点的两条数轴构成平面直角坐标系,但如果平面坐标系中两条坐标轴不垂直,则这样的坐标系称为“斜坐标系”.如图,在斜坐标系中,过点作两坐标轴的平行线,其在轴和轴上的截距分别作为点的坐标和坐标,记.若斜坐标系中,轴正方向和轴正方向的夹角为 , 则该坐标系中和两点间的距离为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、已知向量 , 且在上的投影向量为 , 则与的夹角为( )A、 B、 C、 D、
-
15、已知等边三角形的边长是 , 、分别是、的中点,则( )A、 B、 C、 D、
-
16、已知 , , , 若 , , 三点共线,则( )A、 B、 C、 D、2
-
17、在中, , , 则的值为( )A、2 B、3 C、4 D、5
-
18、已知在平面四边形中, , , . 将沿BD翻折至 , , 点在线段BD上,且 , .(1)、求证:面;(2)、求三棱锥外接球的半径;(3)、求直线CF与平面所成角的正弦值的取值范围.
-
19、每年的10月1日是国庆节,为庆祝该节日,某学校举办了“知识竞赛”.竞赛共分两轮,即每位参赛选手均须参加两轮比赛,已知在第一轮比赛中,选手甲,乙胜出的概率分别为 , ;在第二轮比赛中,选手甲,乙胜出的概率分别为p,q.假设甲,乙两人在每轮比赛中是否胜出互不影响.(1)、若 , 求乙恰好有一轮胜出的概率;(2)、若甲,乙各有一轮胜出的概率为 , 甲,乙两轮都胜出的概率为 .
①求p,q的值;
②求甲,乙两人至少有一人两轮都胜出的概率.
-
20、在中,角A,B,C所对的边分别为a,b,c,且 .(1)、求角B;(2)、若的角平分线交AC于点D, , , 求BD;(3)、若的外接圆的半径为 , 求的取值范围.