相关试卷
-
1、已知函数.(1)、求的定义域;(2)、证明:在上单调递减.
-
2、已知函数的图像关于点对称,且在上有且只有两条对称轴,则.
-
3、命题“ , ”的否定是.
-
4、.
-
5、已知 , 则( )A、的最小正周期是 B、在上单调递减 C、直线是图象的一条对称轴 D、在上的所有零点和为
-
6、设函数.若 , 且 , 则( )A、 B、 C、 D、
-
7、下列函数中,为奇函数且在上单调递增的是( )A、 B、 C、 D、
-
8、若关于x的不等式在上恒成立,则m的取值范围是( )A、 B、 C、 D、
-
9、已知 , , , 则( )A、 B、 C、 D、
-
10、已知函数 , 则( )A、在上单调递增且值域为 B、在上单调递减且值域为 C、在上单调递增且值域为 D、在上单调递减且值域为
-
11、已知 , 则( )A、 B、 C、 D、
-
12、函数的图象大致形状是( )A、
 B、
B、 C、
C、 D、
D、
-
13、若扇形的面积为1cm2 , 周长为4cm,则扇形圆心角的弧度数为( )A、1 B、2 C、3 D、4
-
14、已知集合 , 则( )A、 B、 C、或 D、或
-
15、长度为6的线段 , 设线段中点为G,线段的两个端点P和Q分别在x轴和y轴上滑动.(1)、求点G的轨迹方程;(2)、设点G的轨迹与x轴交点分别为A,B(A点在左),与y轴交点分别为C,D(C点在上),设H为第一象限内点G的轨迹上的动点,直线与直线交于点M,直线与直线交于点N.试判断直线与的位置关系,并证明你的结论.
-
16、已知圆心为的圆经过点和 , 且圆心在直线上.(1)、求圆的标准方程及过点的切线方程;(2)、直线与圆相交于两点,且 , 求实数的值.
-
17、已知空间内三点 , , .(1)、求以向量 , 为一组邻边的平行四边形的面积;(2)、若向量与向量 , 都垂直,且 , 求向量的坐标.
-
18、已知圆 , 圆 , 分别为圆和圆上的动点,为直线上的动点,则的最小值为 .
-
19、如图所示,一隧道内设双行线公路,其截面由一段圆弧和一个长方形构成.已知隧道总宽度AD为m,行车道总宽度BC为m,侧墙EA、FD高为2m,弧顶高MN为5m.为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5m.请计算车辆通过隧道的限制高度是 .
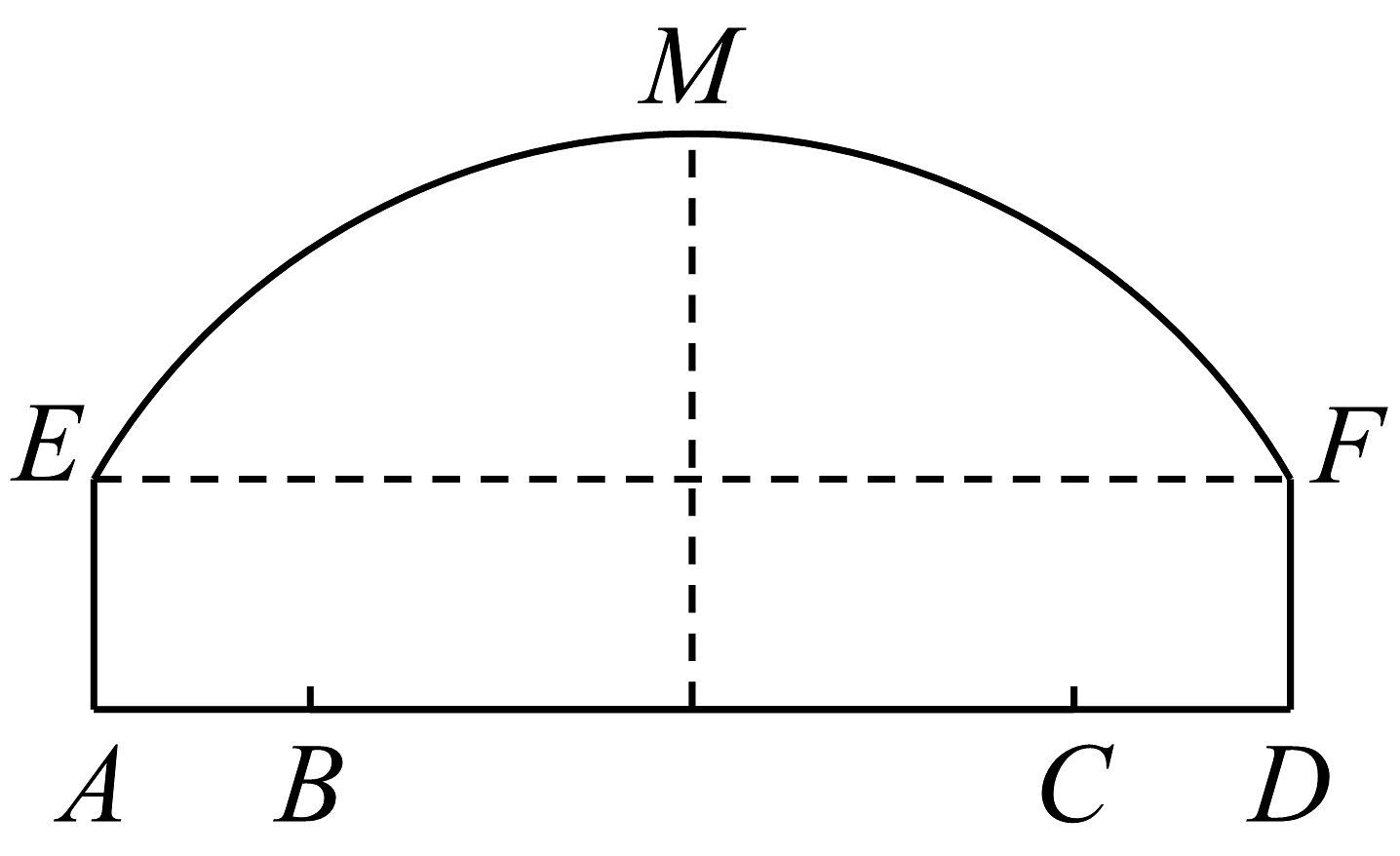
-
20、给出下列命题,其中正确的命题是( )A、若 , 则或 B、若向量是向量的相反向量,则 C、在正方体中, D、若空间向量、、满足 , , 则