相关试卷
-
1、已知函数且.若 , 则.
-
2、“阿基米德多面体”也称半正多面体,是由两种或多种正多边形面组成,而又不属于正多面体的凸多面体,体现了数学的对称美.如图,某广场的一张石凳就是一个阿基米德多面体,它是由正方体截去八个一样的四面体得到的二十四等边体,若它所有的棱长都为2,则( )
 A、该石凳的表面积为 B、该石凳的体积为 C、直线与的夹角为 D、平面
A、该石凳的表面积为 B、该石凳的体积为 C、直线与的夹角为 D、平面 -
3、已知、是椭圆的左、右焦点,点在上,是上的动点,轴,垂足为 , 且为的中点,则( )A、的最大值为 B、的最小值为 C、点的轨迹方程为 D、的最小值为
-
4、已知函数 , 则( )A、函数为偶函数 B、曲线的一个对称中心为 C、在区间单调递增 D、的最大值为2
-
5、设函数 , 其中 , 若 , 则( )A、2 B、4 C、6 D、8
-
6、如图,在等边中, , 以为直径分别作半圆,是两段半圆弧上的动点,则的取值范围是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
7、设函数是奇函数, , 若 , 则( )A、 B、0 C、1 D、2
-
8、的展开式中,含的项的系数是( )A、 B、 C、30 D、60
-
9、已知数据的方差 , 则( )A、 B、 C、1 D、0
-
10、复数满足 , 则在复平面内对应的点的轨迹为( )A、圆 B、双曲线的一支 C、椭圆 D、抛物线
-
11、已知集合 , 则( )A、 B、 C、 D、
-
12、定义:若非零向量 , 函数的解析式满足 , 则称为的“线性函数”,为的“线性向量”,(1)、若向量为函数的“线性向量”,求(2)、若函数为向量的“线性函数”,在中, , 且 , 求的值;(3)、若函数为向量的“线性函数”,且当时,方程存在4个不相等的实数根,求实数的取值范围.
-
13、如图,在正四棱锥中,所有棱长均为 , 点是棱的中点,点是底面内任意一点,点到侧面的距离分别为 .
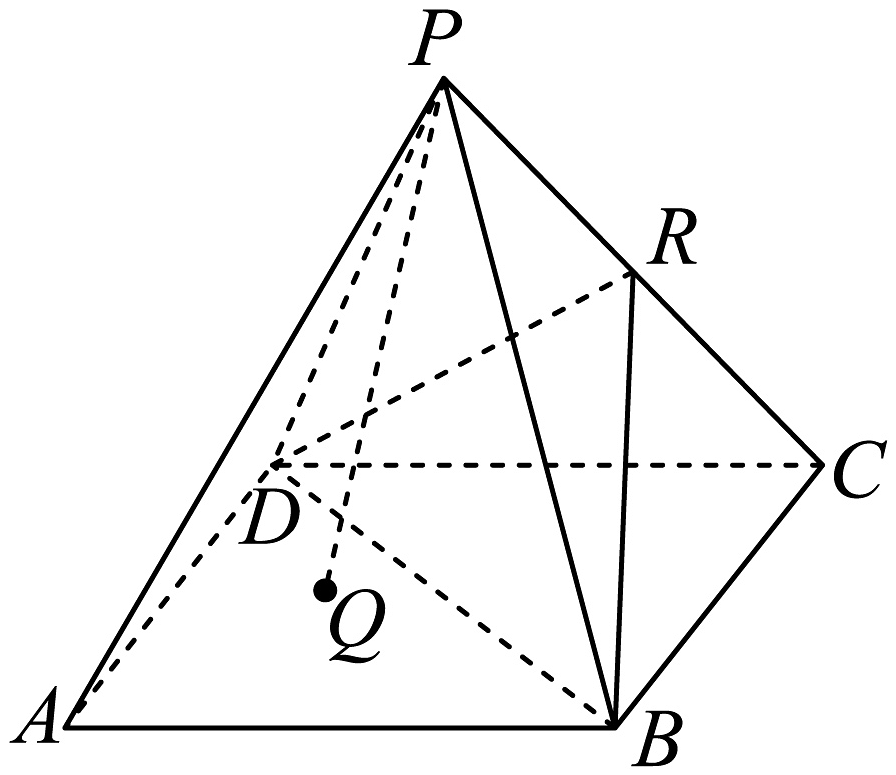 (1)、证明:平面平面;(2)、求;(3)、记与侧面所成的角分别为 , 证明: .
(1)、证明:平面平面;(2)、求;(3)、记与侧面所成的角分别为 , 证明: . -
14、在中,角 , , 的对应边分别为 , , , .(1)、求;(2)、若 , , 求的面积.
-
15、已知复数和它的共轭复数满足.(1)、求;(2)、若是关于的方程的一个根,求复数的模长.
-
16、已知向量 , , 且与垂直.(1)、求;(2)、若与互相垂直,求实数的值.
-
17、已知 , 且为第三象限角,则.
-
18、三棱锥中,顶点P在平面ABC的射影为O,满足 , A点在侧面PBC上的射影H是的垂心, , 此三棱锥体积的最大值是.
-
19、如图,在平面直角坐标系中, , 则下列说法正确的有( )
 A、 B、四边形的面积为 C、外接圆的周长为 D、
A、 B、四边形的面积为 C、外接圆的周长为 D、 -
20、已知且 , 点为线段上的动点, , 则下列结论正确的是( )A、 B、若为线段的中点,则 C、 D、的取值范围为