版本：

全部人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）上教版（2020）人教新课标A版人教新课标B版苏教版北师大版湘教版沪教版人教版（旧版）

相关试卷

1、在 $Rt △ A B C$ 中，内角 $A, B, C$ 的对边分别为 $a, b, c$ ，已知 $\frac{\cos A}{a} = \frac{\cos B + \cos C}{b + c} .$

(1)、求角 $A$ ；

(2)、已知 $c \neq 2 b, a = 2 \sqrt{3}$ ，点 $P, Q$ 是边 $A C$ 上的两个动点（ $P, Q$ 不重合），记 $∠ P B Q = θ$ .
①当 $θ = \frac{π}{6}$ 时，设 $△ P B Q$ 的面积为 $S$ ，求 $S$ 的最小值：
②三角和差化积公式是一组应用广泛的三角恒等变换式，其形式如图：
$\sin α \cdot \cos β = \frac{1}{2} [\sin (α + β) + \sin (α - β)]$
$\cos α \cdot \sin β = \frac{1}{2} [\sin (α + β) - \sin (α - β)]$
$\cos α \cdot \cos β = \frac{1}{2} [\cos (α + β) + \cos (α - β)]$
$\sin α \cdot \sin β = - \frac{1}{2} [\cos (α + β) - \cos (α - β)]$
它在工程学、绘图测量学等方面，有着广泛的应用．现记 $∠ B P Q = α, ∠ B Q P = β$ ，请利用该公式，探究是否存在实常数 $θ$ 和 $k$ ，对于所有满足题意的 $α, β$ ，都有 $\sin 2 α + \sin 2 β + k = 4 k \sin α \sin β$ 成立？若存在，求出 $θ$ 和 $k$ 的值；若不存在，说明理由．

查看解析
2、某小区拟用一块半圆形地块（如图所示）建造一个居民活动区和绿化区．已知半圆形地块的直径 $A B = 4$ 千米，点 $O$ 是半圆的圆心，在圆弧上取点 $C$ 、 $D$ ，使得 $B C = D C$ ，把四边形 $A B C D$ 建为居民活动区，并且在居民活动区周围铺上一条由线段 $A B$ ， $B C$ ， $C D$ 和 $D A$ 组成的塑胶跑道，其它部分建为绿化区．设 $∠ C O B = θ$ ，且 $\frac{π}{6} \leq θ < \frac{π}{2}$ ；

(1)、求塑胶跑道的总长 $l$ 关于 $θ$ 的函数关系式；

(2)、当 $θ$ 为何值时，塑胶跑道的总长 $l$ 最长，并求出 $l$ 的最大值．

查看解析
3、在 $△ A B C$ 中，已知 $A B = 4$ ， $A C = 10$ ， $∠ B A C = 60^{\circ}$ ， $B C$ 、 $A C$ 边上的两条中线 $A M$ 、 $B N$ 相交于点 $G$ .

(1)、求 $B N$ 、 $A M$ 的长；

(2)、求 $∠ M G N$ 的余弦值.

查看解析
4、已知 $|\vec{a}| = 4, |\vec{b}| = 3, (2 \vec{a} - 3 \vec{b}) \cdot (2 \vec{a} + \vec{b}) = 13$ ．

(1)、求 $\vec{a}$ 与 $\vec{b}$ 的夹角；

(2)、若 $\vec{a}$ 在 $\vec{b}$ 方向上的投影向量为 $\vec{c}$ ，求 $\vec{c} \cdot (\vec{a} + \vec{b})$ 的值．

查看解析
5、已知 $\tan (α + \frac{π}{6}) = \frac{1}{2}$ ， $\tan (\frac{π}{12} + β) = \frac{1}{3}$ ，则 $\tan (α - 2 β) =$ ．

查看解析
6、若 $z \in C$ 且 $|z| = 1$ ，则 $|z - 1 - 2 i|$ 的最小值是．

查看解析
7、如图所示，已知角 $α, β (0 < α < β < \frac{π}{2})$ 的始边为 $x$ 轴的非负半轴，终边与单位圆的交点分别为 $A, B$ ， $M$ 为线段 $A B$ 的中点，射线 $O M$ 与单位圆交于点 $C$ ，则（）

A、 $∠ A O B = β - α$ B、 $|O M| = cos \frac{β - α}{2}$ C、点 $C$ 的坐标为 $(cos \frac{α + β}{2}, sin \frac{α + β}{2})$ D、点 $M$ 的坐标为 $(cos \frac{α + β}{2} cos \frac{β - α}{2}, sin \frac{α + β}{2} sin \frac{β - α}{2})$

查看解析
8、在 $△ A B C$ 中，角 $A, B, C$ 所对的边分别为 $a, b, c$ ，已知 $(a + b) : (b + c) : (c + a) = 5 : 6 : 7$ ，则下列结论正确的是（）

A、 $sin A : sin B : sin C = 2 : 3 : 4$ B、 $△ A B C$ 为钝角三角形 C、若 $a = 6$ ，则 $△ A B C$ 的面积是 $6 \sqrt{15}$ D、若 $△ A B C$ 外接圆半径是 $R$ ，内切圆半径为 $r$ ，则 $\frac{R}{r} = \frac{16}{5}$

查看解析
9、已知复数 $z_{1}, z_{2}$ 是关于 $x$ 的方程 $x^{2} + b x + 1 = 0 (- 2 < b < 2, b \in R)$ 的两根，则下列说法中正确的是（）

A、 ${\bar{z}}_{1} = z_{2}$ B、 $\frac{z_{1}}{z_{2}} \in R$ C、 $|z_{1} \cdot z_{2}| = 1$ D、若 $b = 1$ ，则 $z_{1}^{3} = z_{2}^{3} = 1$

查看解析
10、“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的 $logo$ 很相似，故形象地称其为“奔驰定理”.奔驰定理：已知 $O$ 是 $△ A B C$ 内的一点， $△ B O C$ ， $△ A O C$ ， $△ A O B$ 的面积分别为 $S_{A}, S_{B}, S_{C}$ ，则有 $S_{A} \cdot \vec{O A} + S_{B} \cdot \vec{O B} + S_{C} \cdot \vec{O C} = \vec{0}$ .设 $O$ 是锐角 $△ A B C$ 内的一点， $∠ B A C$ ， $∠ A B C$ ， $∠ A C B$ 分别是 $△ A B C$ 的三个内角，以下命题正确的有（）

A、若 $\vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$ ，则 $O$ 为 $△ A B C$ 的重心 B、若 $\vec{O A} + \vec{2 O B} + 3 \vec{O C} = \vec{0}$ ，则 $S_{A} : S_{B} : S_{C} = 1 : 2 : 3$ C、若 $| \vec{O A} | = | \vec{O B} | = 2$ ， $∠ A O B = \frac{5 π}{6}$ ， $2 \vec{O A} + 3 \vec{O B} + 4 \vec{O C} = \vec{0}$ ，则 $S_{△ A B C} = \frac{9}{2}$ D、若 $O$ 为 $△ A B C$ 的垂心，则 $\tan ∠ B A C \cdot \vec{O A} + \tan ∠ A B C \cdot \vec{O B} + \tan ∠ A C B \cdot \vec{O C} = \vec{0}$

查看解析
11、分别以锐角三角形 $A B C$ 的边AB，BC，AC为旋转轴旋转一周后得到的几何体体积之比为 $\sqrt{3} : \sqrt{6} : 2$ ，则 $\cos B =$ （）

A、 $\frac{5 \sqrt{3}}{12}$ B、 $\frac{5 \sqrt{2}}{12}$ C、 $\frac{3 \sqrt{2}}{8}$ D、 $\frac{\sqrt{6}}{12}$

查看解析
12、已知正三角形 $A B C$ 的边长为2，动点 $P$ 满足 $|P C| = 1$ ，则 $\vec{P A} \cdot \vec{P B}$ 的最小值为（）

A、 $4 - 2 \sqrt{2}$ B、 $3 - 2 \sqrt{2}$ C、 $3 - 2 \sqrt{3}$ D、 $4 - 2 \sqrt{3}$

查看解析
13、已知 $\overset{⃑}{a}$ ， $\overset{⃑}{b}$ 为不共线向量，且 $\overset{⃑}{A B} = 2 \overset{⃑}{a} + \overset{⃑}{b}$ ， $\overset{⃑}{B C} = - \overset{⃑}{a} + 4 \overset{⃑}{b}$ ， $\overset{⃑}{C D} = 3 (\overset{⃑}{a} - \overset{⃑}{b})$ ，则（）

A、 $A$ 、 $B$ 、 $C$ 三点共线 B、 $A$ 、 $B$ 、 $D$ 三点共线 C、 $B$ 、 $C$ 、 $D$ 三点共线 D、 $A$ 、 $C$ 、 $D$ 三点共线

查看解析
14、已知向量 $\vec{a} = (1, 2), \vec{b} = (- 1, 1), \vec{c} = (m, 2)$ ，且 $(\vec{a} - 2 \vec{b}) ⊥ \vec{c}$ ，则实数 $m =$ （）

A、-1 B、0 C、1 D、任意实数

查看解析
15、复数 $z = (2 - i) (|4 - 3 i| + i)$ 的共轭复数为（）

A、 $11 + 3 i$ B、 $51 + 23 i$ C、 $9 + 3 i$ D、 $49 + 23 i$

查看解析
16、已知关于 $x$ 的不等式 $a x^{2} + b x + c > 0$ 的解集为 ${x ∣ - 2 < x < 7}$ ，其中 $a, b, c$ 为常数，则不等式 $c x^{2} + b x + a \leq 0$ 的解集是（）

A、 $\{x |- \frac{1}{2} \leq x \leq \frac{1}{7}\}$ B、 $\{x |x \leq - \frac{1}{7}$ ，或 $x \geq \frac{1}{2}\}$ C、 $\{x |x \leq - \frac{1}{2}$ ，或 $x \geq \frac{1}{7}\}$ D、 $\{x |- \frac{1}{7} \leq x \leq \frac{1}{2}\}$

查看解析
17、若复数z满足 $(1 + z) (1 - i) = 2$ ，则复数z的虚部为（）

A、i B、－i C、1 D、－1

查看解析
18、三棱台 $A B C - A_{1} B_{1} C_{1}$ 的底面是正三角形， $A A_{1} ⊥$ 平面 $A B C$ ， $A B = 4$ ， $A_{1} B_{1} = 2$ ， $A A_{1} = \sqrt{3}$ ， E是 $A B$ 的中点，平面 $A_{1} C_{1} E$ 交平面 $A B C$ 于直线l．

(1)、求证： $A C ∥ l$ ；

(2)、求直线 $B_{1} C$ 与平面 $A_{1} C_{1} E$ 所成角的正弦值．

查看解析
19、已知函数 $f (x) = 2 \sin (ω x + φ)$ （ $ω > 0$ ， $| φ | < π$ ）的图象如图所示，点 $A (0, - 1)$ ， $B (x_{0}, 1)$ 在曲线 $f (x)$ 上，若 $| A B | = \sqrt{13}$ ，则（）

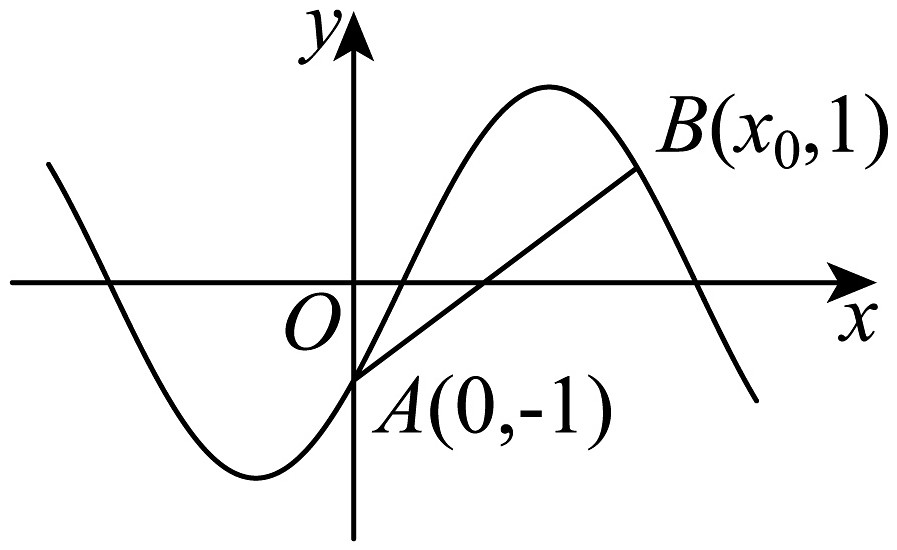A、 $φ = - \frac{π}{6}$ B、 $f (x)$ 的图象关于点 $(\frac{1}{2}, 0)$ 对称 C、 $f (x)$ 在 $[7, 11]$ 上单调递减 D、若将 $f (x)$ 图象每个点的横坐标变为原来的 $\frac{π}{t} (t > 0)$ 倍后在 $(0, 2 π)$ 上有且仅有2个极值点，则 $t \in (\frac{5}{2}, 4]$

查看解析
20、下列说法中正确的是（）

A、若随机变量 $X \sim B (10, p)$ ，且 $E (X) = 3$ ，则 $D (X) = 2.1$ B、某射击运动员在一次训练中 $10$ 次射击成绩 $（$ 单位：环 $）$ 如下： $6$ ， $5$ ， $7$ ， $9$ ， $6$ ， $8$ ， $9$ ， $7$ ， $9$ ， $5$ ，这组数据的 $75$ 百分位数为 $7$ C、若随机变量 $ξ \sim N (μ, σ^{2})$ ，且 $P (ξ > 3) = P (ξ < - 1) = p$ ，则 $P (1 \leq ξ \leq 3) = \frac{1}{2} - p$ D、若变量y关于变量x的线性回归方程为 $\hat{y} = x + t$ ，且 $\bar{x} = 4$ ， $\bar{y} = 2 t$ ，则 $t = \frac{4}{3}$

查看解析

上一页 1033 1034 1035 1036 1037 下一页跳转