-
1、已知点 , 圆: .(1)、求圆过点的最短弦所在的直线方程;(2)、若圆与直线相交于 , 两点,为原点,且 , 求的值.
-
2、已知直线: , 经过点 .(1)、若 , 求直线的方程;(2)、在(1)的条件下,求与之间的距离;(3)、若与轴、轴的正半轴交于 , 两点,求的最小值.
-
3、已知空间三点 , , , 设 , .(1)、求的值;(2)、若向量与互相垂直,求实数的值.
-
4、点在椭圆上,是椭圆的一个焦点,为的中点,若 , 则 .
-
5、直线的倾斜角为 .
-
6、如图,直三棱柱中, , , , 分别为棱和的中点,为棱上的动点,则下列说法正确的是( )
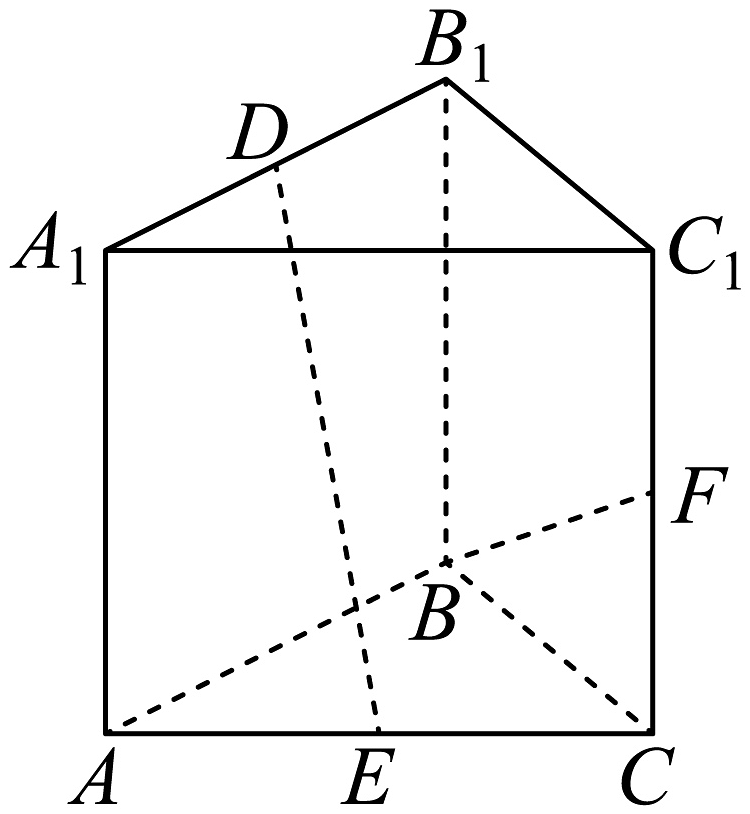 A、 B、该三棱柱的体积为4 C、直线与平面所成角的正切值的最大值为 D、过 , , 三点截该三棱柱的截面面积为
A、 B、该三棱柱的体积为4 C、直线与平面所成角的正切值的最大值为 D、过 , , 三点截该三棱柱的截面面积为 -
7、已知直线: , 则下列说法正确的是( )A、点到直线的距离为 B、直线的截距式方程为 C、直线的一个方向向量为 D、若直线与圆相切,则
-
8、已知圆:与圆:有两条公切线,则实数的取值范围( )A、 B、 C、 D、
-
9、如图,在三棱锥中,已知是上靠近的三等分点,是的中点,则( )
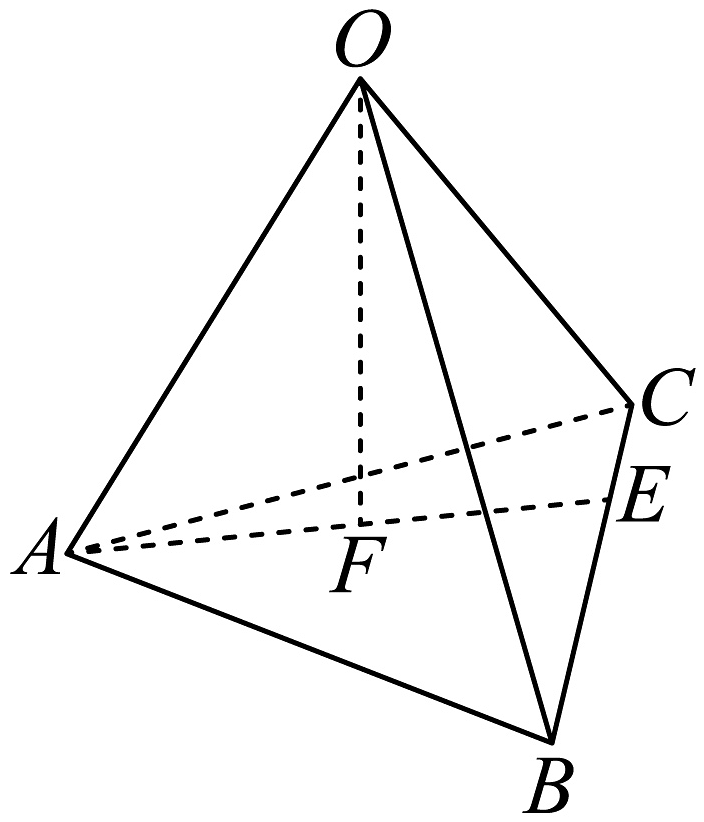 A、 B、 C、 D、
A、 B、 C、 D、 -
10、经过点作圆的切线,则切线方程为( )A、 B、 C、 D、
-
11、已知 , 分别为椭圆的左右焦点,为椭圆上一点,若 , 则为( )A、1 B、4 C、6 D、7
-
12、已知直线:与: , 若 , 则为( )A、 B、0 C、 D、
-
13、已知直线过、两点,则该直线的斜率为( )A、 B、 C、 D、
-
14、对于数集M,定义M的特征函数: , 对于两个数集 , 定义.(1)、已知集合 ,
(i)求的值,并用列举法表示;
(ii)若用表示有限集合M所包含的元素个数,已知集合X是正整数集的子集,求的最小值(无需证明);
(2)、证明:. -
15、已知是定义在上的函数,若满足且.(1)、求的解析式;(2)、判断的单调性,并利用定义证明你的结论;(3)、设函数 , 若对都有成立,求的取值范围.
-
16、习近平总书记一直重视生态环境保护,十八大以来多次对生态文明建设作出重要指示,在不同场合反复强调“绿水青山就是金山银山”,随着中国经济的快速发展,环保问题已经成为一个不容忽视的问题.某污水处理厂在国家环保部门的支持下,引进新设备,新上了一个从生活垃圾中提炼化工原料的项目.经测算,该项目月处理成本(元)与月处理量(吨)之间的函数关系可以近似地表示为 , 且每处理一吨生活垃圾,可得到能利用的化工原料的价值为400元.(1)、当时,判断该项目能否获利,如果获利,求出最大利润.(2)、该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
-
17、已知函数 .(1)、当时,函数在上单调,求b的取值范围;(2)、若的解集为 , 求关于x的不等式的解集.
-
18、已知集合为全体实数集,集合或 , .(1)、若 , 求和;(2)、若 , 求的取值范围.
-
19、已知 , 集合 , 集合 , 若中恰有两个整数,则实数的取值范围是.
-
20、已知是定义域为的偶函数,在上为单调增函数,且 , 则不等式的解集为 .