相关试卷
- 浙江省宁波市北仑区2017-2018学年九年级上学期科学期末考试试卷
- 浙江省宁波市江北区2017-2018学年九年级上学期科学期末考试试卷
- 浙江省宁波市鄞州区九校2017-2018学年八年级上学期科学期末考试试卷
- 浙江省宁波市东钱湖九校2017-2018学年七年级上学期科学期中联考试卷
- 浙江省宁波市海曙区2017-2018学年九年级上学期科学期中统考试卷
- 浙江省宁波鄞州区九校2017-2018学年九年级上学期科学月考试卷
- 浙江省宁波鄞州区九校2017-2018学年七年级上学期科学第一次月考试卷
- 浙江省宁波鄞州区九校2017-2018学年八年级上学期科学第一次月考试卷
- 2017-2018学年华师大版八年级上学期科学期中模拟试卷
- 2017-2018学年华师大版九年级上学期科学期中模拟试卷
-
1、酸的共性实质上就是的性质,酸的个性实质上是的性质
-
2、酸的个性
盐酸
浓盐酸具有性
与硝酸银溶液反应,生成
硫酸
浓硫酸具有、、腐蚀性
与硝酸钡溶液反应,生成
-
3、酸的通性
酸的通性
反应情况
化学方程式
(1)能与指示剂作用
能使紫色石蕊试液变 , 不能使无色酚酞试液变色
/ (2)能与活泼金属反应
生成盐和氢气
(3)能与金属氧化物反应
生成盐和水
+
(4)能与碱反应
生成盐和水
(5)能与某些盐反应
生成新盐和新酸
-
4、如图所示为甲、乙、丙三种物质的转化关系(“→”表示反应一步实现,反应条件略去),下列各组物质中不能实现该转化关系的是( )
选项
甲
乙
丙

A
C
CO2
co
B
Zn
ZnO
Zn(NO3)2
C
Ca(OH)2
CaCO3
CaCl2
D
KOH
KNO3
K2SO4
A、A B、B C、C D、D -
5、将一定质量的铁粉加入Mg(NO3)2和Cu(NO3)2 的混合溶液中,充分反应后过滤,得滤渣和滤液。下列说法正确的是 ( )A、滤渣质量与加入的铁粉质量可能相等 B、滤液中一定有 Mg(NO3)2、 Fe(NO3)2 , 可能有 Cu(NO3)2 C、若加入的铁粉过量,则得到的滤液呈无色 D、若向滤渣中加入稀盐酸,有气泡生成,则滤渣中一定有 Cu、 Fe、 Mg
-
6、锰(Mn)和镍(Ni)是两种不常见的金属,为了比较锰、镍和铁的金属活动性,小明在老师的指导下进行了实验,结果如下表:
项目
加金属锰
加金属铁
加金属镍
硝酸锰溶液
有金属析出
无金属出现
则三种金属的活动性顺序为 ( )
A、Fe> Ni> Mn B、Mn> Fe> Ni C、Ni> Mn> Fe D、Fe> Mn> Ni -
7、如图是小科组装的实验装置,小科在a装置的锥形瓶中加入了一定量的金属锌,将针管中的稀盐酸注入锥形瓶中,观察到 b 装置中液面____(填“左高右低”“左低右高”或“不变”);下列药品组合也能产生同样现象的是____(填字母)。
 A、稀盐酸和金属铜 B、氢氧化钠固体和水
A、稀盐酸和金属铜 B、氢氧化钠固体和水 -
8、将质量相等的 Mg、 Al、 Zn三种金属分别放入质量和质量分数均相等的三份稀硫酸中,反应结束后,生成氢气的质量关系不可能是图中的 ( )A、
 B、
B、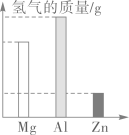 C、
C、 D、
D、
-
9、将 A、B 两种金属分别放入等质量且等质量分数的稀硫酸中,生成氢气的质量与反应时间的关系如图所示,下列结论合理的是( )
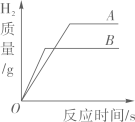 A、金属活动性:A>B B、相对原子质量:A<B C、与金属 A 反应的硫酸一定是过量的 D、与金属B反应的硫酸一定是过量的
A、金属活动性:A>B B、相对原子质量:A<B C、与金属 A 反应的硫酸一定是过量的 D、与金属B反应的硫酸一定是过量的 -
10、判断下列说法的正误,并对错误的说法分析指正。(1)、有单质和化合物生成的反应一定是置换反应
分析指正:。
(2)、在金属活动性顺序中,排在前面的金属都能把排在后面的金属从其盐溶液中置换出来分析指正:。
(3)、等质量的镁和铝与足量稀硫酸反应,镁生成的氢气比铝少分析指正:。
(4)、铁锈能阻止铁继续被锈蚀分析指正:。
(5)、铝比铁耐腐蚀是因为铝不如铁活泼分析指正:。
(6)、氢气、一氧化碳、炭粉分别与黑色的氧化铜反应,都发生了置换反应分析指正:。
(7)、有机化合物中都含有碳元素分析指正:。
(8)、含有氧元素的化合物即为氧化物分析指正:。
(9)、混合物一定是由多种元素组成的分析指正:。
-
11、

-
12、
反应类型
概念
特点
形式
反应
由两种或两种以上物质生成一种物质的反应
多变一
A+B+……→C
反应
由一种物质生成两种或两种以上物质的反应
一变多
A→B+C+……
反应
由一种单质跟一种化合物发生反应生成另一种单质和另一种化合物的反应
单换单
AB+C→A+CB
反应
两种化合物互相交换成分生成两种新化合物的反应
两交换价不变
AB+CD→AD+CB
-
13、
 (1)、在金属的活动性顺序中,金属位置越靠前,活动性就越。(2)、排在氢的金属可以把酸(非氧化性酸)里的氢置换出来,而排在氢的金属不能把酸(非氧化性酸)里的氢置换出来。这里的酸通常指盐酸和稀硫酸而不是浓硫酸(或硝酸),因为金属与浓硫酸(或硝酸)等反应不产生氢气。(3)、一种活动性较的金属能把另一种活动性较的金属从它的盐的水溶液中置换出来。(4)、三种金属的活动性太强,在与盐溶液反应时,会先与溶液中的水发生反应,生成对应的碱和 H2 , 碱再与盐发生复分解反应。
(1)、在金属的活动性顺序中,金属位置越靠前,活动性就越。(2)、排在氢的金属可以把酸(非氧化性酸)里的氢置换出来,而排在氢的金属不能把酸(非氧化性酸)里的氢置换出来。这里的酸通常指盐酸和稀硫酸而不是浓硫酸(或硝酸),因为金属与浓硫酸(或硝酸)等反应不产生氢气。(3)、一种活动性较的金属能把另一种活动性较的金属从它的盐的水溶液中置换出来。(4)、三种金属的活动性太强,在与盐溶液反应时,会先与溶液中的水发生反应,生成对应的碱和 H2 , 碱再与盐发生复分解反应。注意:①置换反应中金属(钾、钙、钠除外)的活动性必须要强于盐中金属阳离子对应的金属;盐必须。
②Fe若参与反应,一定生成(填‘“Fe2+”或
③在金属活动性顺序中,距离的优先置换(例:将铁加入硝酸铜和硝酸银的混合溶液中,铁先置换出银)。
-
14、金属与稀盐酸或稀硫酸的反应
金属
现象
化学方程式(以稀硫酸为例)
镁
剧烈反应,产生大量气泡,溶液呈无色
铝
打磨过的铝放入酸中,剧烈反应,产生大量气泡,溶液呈无色
锌
反应较快,产生大量气泡,溶液呈无色
铁
有少量气泡产生,反应慢,溶液由无色变为色
铜
无任何现象
-
15、金属与氧气的反应
反应条件
金属
现象
化学方程式
常温
镁
打磨过的镁带在空气中表面逐渐变暗
铝
打磨过的铝在空气中表面逐渐变暗,生成一层致密的
点燃或加热
铁
常温下在干燥的空气中,铁很难与氧气反应,点燃后在氧气中能剧烈燃烧, , 生成 , 放出大量的热
铜
常温下在干燥的空气中很难反应,在空气中加热表面会生成黑色物质
高温下不反应
金
在空气中加热不变色
-
16、自然界中有许多“电鱼”,它们身体中的发电器官能产生电。研究表明,某电鱼在水中放电时(图甲),身体AB 段可看成电源和电阻(R1)两部分串联而成,其余部分和水的电阻为 R2 , 它们共同构成闭合电路,简化电路如图乙所示。电鱼放电时的电压(即电源电压)为U,电阻 为获得U 的大小,研究人员通过在水里加入氯化钠来改变R2 , 得到 A、B 两点间电压UAB和电路中电流I 的关系,如图丙所示。电鱼每次放电电压视为相同,电鱼的电阻不变。

请回答:
(1)、向水里加入氯化钠,目的是(填“增大”或“减小”)电阻R2。(2)、求电鱼放电时电压U 的大小。(3)、当 求电鱼放电时R2的电功率P2。 -
17、小科在“测量小灯泡的电功率”实验中,所用实验器材有:电压恒为3 V的电源一个,小灯泡(额定电压为2.5V)、电压表、电流表、滑动变阻器、开关各一个,导线若干。
 (1)、如图3-ZM-5甲所示是小科连接的实物电路,图中有一根导线连接错误,请你在连接错误的导线上打“×”并补画出正确的连线。(2)、电路连接正确后,发现接通开关,调节电路后电压表示数为2 V;接下来小科应该如何操作?。(3)、小科根据记录的多组Ⅰ、U数据,画出了通过小灯泡的电流随其两端电压变化的关系图像(如图乙所示),则小灯泡的额定功率为W。(4)、小科根据小灯泡的 I-U图像(如图乙所示),分析出小灯泡的电阻在增大,你认为原因是。
(1)、如图3-ZM-5甲所示是小科连接的实物电路,图中有一根导线连接错误,请你在连接错误的导线上打“×”并补画出正确的连线。(2)、电路连接正确后,发现接通开关,调节电路后电压表示数为2 V;接下来小科应该如何操作?。(3)、小科根据记录的多组Ⅰ、U数据,画出了通过小灯泡的电流随其两端电压变化的关系图像(如图乙所示),则小灯泡的额定功率为W。(4)、小科根据小灯泡的 I-U图像(如图乙所示),分析出小灯泡的电阻在增大,你认为原因是。 -
18、关于温度、热量、内能,下列说法正确的是 ( )A、0℃的冰没有内能 B、冰熔化时虽然温度保持不变,但它的内能增加 C、物体的温度越高,所含的热量越多 D、只要物体的温度不变,物体的内能就一定不变
-
19、图甲是某兴趣小组设计的一款“高空修枝”工具的示意图。使用时,一只手握紧杆子保持静止,另一只手用F1的力缓慢拉绳子,带动滑轮组工作,在A 点产生的拉力为 F2 , 从而使修剪刀绕O点转动,其刀口对树枝的力为 F3。某时刻,弹簧处于原长,若修剪刀的刀口对树枝施加的力 F3为960 N,F3'是树枝对刀口的力(图乙),此时绳端需施加的力F1为多大?(已知OB=8cm,OC=2cm,滑轮中各股绳子视为平行,工具自重和摩擦忽略不计)

-
20、电气化铁路的高压输电线,无论在严冬还是在酷夏都要绷直,才能使高压线与列车的电极接触良好,这就必须对高压线施加恒定的拉力。为此,工程师设计了如图甲所示的恒拉力系统,其简化原理图如图乙所示。实际测量得到每个水泥块的重力是 120 N。已知某次滑轮组对高压线的拉力至少需要8000 N。
 (1)、A、B、C 中属于动滑轮的是。(2)、计算至少需要悬挂的水泥块个数。(保留整数)(3)、在实际操作中共悬挂了 25 个水泥块,恰好使高压线与列车的电极接触良好。若某段时间内 P 点移动了 20 cm,请求出该过程中水泥块所做的功。
(1)、A、B、C 中属于动滑轮的是。(2)、计算至少需要悬挂的水泥块个数。(保留整数)(3)、在实际操作中共悬挂了 25 个水泥块,恰好使高压线与列车的电极接触良好。若某段时间内 P 点移动了 20 cm,请求出该过程中水泥块所做的功。