相关试卷
- 四川省自贡市2017年高考物理三诊试卷
- 四川省绵阳市三台中学2017-2018学年高二上学期物理开学考试试卷
- 四川省遂宁市2016-2017学年高一上学期物理期末考试试卷
- 四川省南充中学2016-2017学年高一上学期物理期末考试试卷
- 四川省广安市邻水县2016-2017学年高一上学期物理期末考试试卷
- 四川省成都市武侯区2016-2017学年高一上学期物理期末考试试卷
- 四川省南充市2017年高考物理一诊试卷
- 辽宁省锦州市2017年高考物理二模试卷
- 辽宁省大连市金州区得胜高中2016-2017学年高二下学期物理期末考试试卷(选修3-4、选修3-5)
- 辽宁省六校协作体2016-2017学年高一上学期物理期中考试试卷
-
1、对万有引力定律的描述,下列叙述符合史实的是( )A、开普勒通过分析第谷的天文观测数据,发现了万有引力定律 B、丹麦天文学家第谷经过多年的天文观测和记录,提出了“日心说”的观点 C、卡文迪什通过实验推算出来引力常量G的值,被誉为第一个能“称量地球质量”的人 D、由万有引力公式可知,当物体间的距离r趋于零时,万有引力趋于无穷大
-
2、如图所示的游戏装置固定在水平地面上,该装置由水平粗糙直轨道OB、竖直光滑圆弧轨道BCDEF、水平光滑直轨道FM和水平粗糙传送带MN平滑连接而成,其中圆弧轨道BCD与水平轨道FM不交叉。传送带以恒定速度v顺时针转动。一轻质弹簧左端固定,原长时右端处于О点。已知OB段长L1=1m,滑块与OB段的动摩擦因数=0.2,圆弧BCD半径R1=0.8m,圆弧DEF半径R2=0.4m。传送带长L2=3m,滑块与传送带的动摩擦因数=0.4。一质量m=0.5kg的滑块将弹簧压缩至A处(图中未标出,AO段光滑)由静止释放,滑块可视为质点,g取10m/s2 , 不计空气阻力。
 (1)、若弹簧弹性势能Ep=4.5J,求滑块最终静止的位置与管道最低点B的距离;(2)、若弹簧弹性势能Ep=11.25J,求滑块到达竖直光滑圆弧轨道BCD的D点时受到管道作用力大小;(3)、若弹簧弹性势能Ep=11.25J,求滑块平抛的水平距离x与传送带速度大小v的关系。
(1)、若弹簧弹性势能Ep=4.5J,求滑块最终静止的位置与管道最低点B的距离;(2)、若弹簧弹性势能Ep=11.25J,求滑块到达竖直光滑圆弧轨道BCD的D点时受到管道作用力大小;(3)、若弹簧弹性势能Ep=11.25J,求滑块平抛的水平距离x与传送带速度大小v的关系。 -
3、如图所示,倾角θ=30°的足够长斜面固定于水平地面上,将一小球(可视为质点)从斜面底端О以速度v0斜向上方抛出,速度方向与斜面间的夹角为α。经历一段时间,小球以垂直于斜面方向的速度打在斜面上的P点。已知重力加速度为g,不计空气阻力,求:
 (1)、小球抛出时的速度方向与斜面间的夹角α的正切值tanα;(2)、小球到斜面的最大距离;(3)、OP间距离。
(1)、小球抛出时的速度方向与斜面间的夹角α的正切值tanα;(2)、小球到斜面的最大距离;(3)、OP间距离。 -
4、如图所示,斜面ABC中AB段粗糙,BC段光滑。物块以10m/s的初速度从A点沿斜面向上滑行,到达C点速度恰好为零。已知BC段的长度为2m,物块上滑过程中,在AB段的加速度是BC段加速度的1.5倍,且物块在AB段和BC段运动的时间相等,g取10m/s2 , 求:
 (1)、斜面AB段的长度;(2)、物块与斜面AB段间的动摩擦因数。
(1)、斜面AB段的长度;(2)、物块与斜面AB段间的动摩擦因数。 -
5、利用如图甲的实验装置“探究加速度与物体受力、物体质量的关系”。
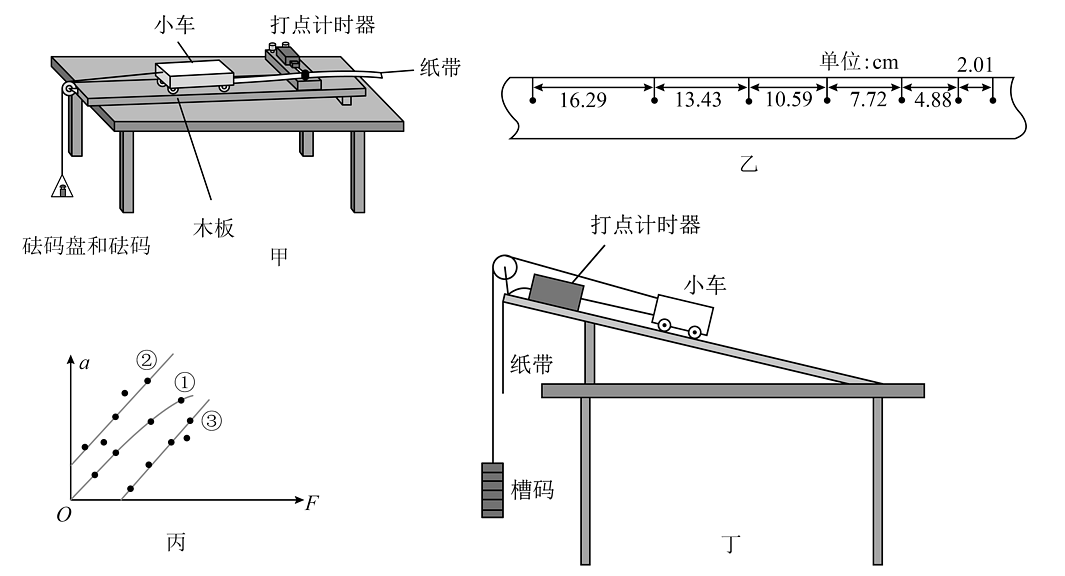 (1)、图乙是实验得到纸带的一部分,每相邻两计数点间有四个点未画出。相邻计数点的间距已在图中给出。打点计时器电源频率为50Hz,则小车的加速度大小为m/s2(结果保留3位有效数字)。(2)、实验得到的理想a-F图像应是一条过原点的直线,但由于实验误差影响,常出现如图丙所示的①、②、③三种情况。下列说法正确的是( )A、图线①的产生原因是摩擦力过大 B、图线②的产生原因是平衡摩擦力时长木板的倾角过大 C、图线③的产生原因是平衡摩擦力时长木板的倾角过大(3)、实验小组的同学觉得用图甲装置测量加速度较大时系统误差较大,所以大胆创新,选用图丁所示器材进行实验,测量小车质量M,所用交流电频率为50Hz,共5个槽码,每个槽码的质量均为m=10g。实验步骤如下:
(1)、图乙是实验得到纸带的一部分,每相邻两计数点间有四个点未画出。相邻计数点的间距已在图中给出。打点计时器电源频率为50Hz,则小车的加速度大小为m/s2(结果保留3位有效数字)。(2)、实验得到的理想a-F图像应是一条过原点的直线,但由于实验误差影响,常出现如图丙所示的①、②、③三种情况。下列说法正确的是( )A、图线①的产生原因是摩擦力过大 B、图线②的产生原因是平衡摩擦力时长木板的倾角过大 C、图线③的产生原因是平衡摩擦力时长木板的倾角过大(3)、实验小组的同学觉得用图甲装置测量加速度较大时系统误差较大,所以大胆创新,选用图丁所示器材进行实验,测量小车质量M,所用交流电频率为50Hz,共5个槽码,每个槽码的质量均为m=10g。实验步骤如下:i.安装好实验器材,跨过定滑轮的细线一端连接在小车上,另一端悬挂着5个槽码。调整轨道的倾角,用手轻拨小车,直到打点计时器在纸带上打出一系列等间距的点,表明小车沿倾斜轨道匀速下滑;
ii.保持轨道倾角不变,取下1个槽码(即细线下端悬挂4个槽码),让小车拖着纸带沿轨道下滑,根据纸带上打的点迹测出加速度a;
iii.逐个减少细线下端悬挂的槽码数量,重复步骤ii;
iv.以取下槽码的总个数n(1≤n≤5)的倒数为横坐标,为纵坐标,在坐标纸上作出关系图线。
已知重力加速度大小g=9.80m/s2 , 计算结果均保留三位有效数字,请完成下列填空:
①写出随变化的关系式(用M,m,g,a,n表示);
②测得关系图线的斜率为2.5s2/m,则小车质量M=kg。
-
6、如图所示,原长为L的弹性轻绳一端固定于天花板上的О点,另一端与水平地面上质量为m的滑块A相连,О点正下方L处有一光滑小钉B位于弹性绳右侧。当弹性绳处于竖直位置时,滑块A对地面的压力等于自身重力的一半。现有一水平拉力F作用在滑块A上,使其向右缓慢运动一段距离后撤去F,此时滑块A恰好能静止在地面上。已知弹性轻绳遵循胡克定律,其弹性势能 , 式中k为弹性绳的劲度系数,x为弹性绳的形变量。此过程中弹性绳始终处于弹性限度内,滑块A与地面间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度大小为g。对于该过程,下列说法正确的是( )
 A、滑块A对地面的压力大小不变 B、滑块A向右运动的距离为 C、滑块A克服摩擦力做的功为 D、拉力F做的功为
A、滑块A对地面的压力大小不变 B、滑块A向右运动的距离为 C、滑块A克服摩擦力做的功为 D、拉力F做的功为 -
7、如图所示,在某行星表面有一倾斜的圆盘,绕垂直于盘面的固定对称轴以恒定角速度转动,盘面与水平面的夹角为30°,质量为m的小物块(可视为质点)距转轴距离为L,与圆盘保持相对静止。已知角速度为时,小物块恰好相对滑动,物块与盘面间的动摩擦因数为(最大静摩擦力等于滑动摩擦力),星球的半径为R,引力常量为G,则下列说法正确的是( )
 A、当物块以角速度随圆盘匀速转动到最高点时,物块所受摩擦力方向沿盘面向下 B、当物体以角速度随圆盘匀速转动到最高点时,物块所受摩擦力大小 C、该行星的第一宇宙速度为 D、该行星的密度为
A、当物块以角速度随圆盘匀速转动到最高点时,物块所受摩擦力方向沿盘面向下 B、当物体以角速度随圆盘匀速转动到最高点时,物块所受摩擦力大小 C、该行星的第一宇宙速度为 D、该行星的密度为 -
8、某种窗户支架如图甲所示,其工作原理简化图如图乙所示。ad杆的a点通过较链固定在滑槽导轨中,d点通过饺链固定在窗户底面,滑块可在滑槽导轨中自由滑动,bc杆的c点通过饺链固定在滑块上,b点通过饺链固定在ad杆上。某次关闭窗户的过程中,ad杆绕a点匀速转动,则下列说法正确的是( )
 A、b点的线速度等于d点的线速度 B、d点的加速度大小不变 C、c点速度大小始终不变 D、b点和c点的速度大小可能相等
A、b点的线速度等于d点的线速度 B、d点的加速度大小不变 C、c点速度大小始终不变 D、b点和c点的速度大小可能相等 -
9、粗糙水平地面上有一质量为M、倾角为30°的粗糙楔形物体C,斜面上有一个质量为2m的物块B,B通过平行于斜面的轻绳绕过定滑轮Р与结点О连接,结点处悬挂一质量为m的小球A。初始时OP间轻绳水平,拉力F与水平方向夹角 , 如图所示。现让拉力F顺时针缓慢转动90°且保持α大小不变,转动过程B、C始终保持静止。下列说法正确的是( )
 A、拉力F一直减小 B、绳对B的拉力一直增大 C、B、C间的摩擦力先增大再减小 D、物体C对地面的压力先增大再减小
A、拉力F一直减小 B、绳对B的拉力一直增大 C、B、C间的摩擦力先增大再减小 D、物体C对地面的压力先增大再减小 -
10、如图所示,与水平面成θ30°角的传送带正以v=10m/s的速度顺时针运行,A、B两端相距l40m。现每隔1s把质量m1kg的工件(视为质点)轻放在传送带上的A端,当每个工件离开B端时恰好在A端放上一个工件,工件与传送带间的动摩擦因数 , g取10m/s2 , 下列说法正确的是( )
 A、传送带上始终有6个工件 B、两个工件间的最小距离为2.5m C、工件在传送带上时,先受到沿传送带向上的摩擦力,后不受摩擦力 D、满载时与空载时相比,电机对传送带的牵引力增大了30N
A、传送带上始终有6个工件 B、两个工件间的最小距离为2.5m C、工件在传送带上时,先受到沿传送带向上的摩擦力,后不受摩擦力 D、满载时与空载时相比,电机对传送带的牵引力增大了30N -
11、如图为电影《流浪地球2》中的“太空电梯”,假若质量为m的宇航员乘坐这种固定在赤道上的“太空电梯”上升,电梯运行到距离地面高度h处停止。已知地球的半径为R,表面的重力加速度为g,自转周期为T,引力常量为G,假若同步卫星距离地面的高度为H,下列说法正确的是( )
 A、宇航员在“太空电梯”中处于静止状态时,处于平衡状态 B、当h=H,万有引力小于宇航员做圆周运动的向心力 C、当h>H,宇航员受到向下的压力为 D、当h<H,宇航员受到向上的支持力为
A、宇航员在“太空电梯”中处于静止状态时,处于平衡状态 B、当h=H,万有引力小于宇航员做圆周运动的向心力 C、当h>H,宇航员受到向下的压力为 D、当h<H,宇航员受到向上的支持力为 -
12、如图所示是运动员将网球在边界A处正上方B点正对球网水平向右击出,恰好过网C的上边沿落在D点的示意图,不计空气阻力,已知AB=h1 , 网高 , AC=x,重力加速度为g,下列说法中正确的是( )
 A、落点D距离网的水平距离为 B、网球的初速度大小为 C、若击球高度低于h1 , 应减小击球速度,才能让球落在对方界内 D、若击球高度低于 , 无论球的初速度多大,球都不可能落在对方界内
A、落点D距离网的水平距离为 B、网球的初速度大小为 C、若击球高度低于h1 , 应减小击球速度,才能让球落在对方界内 D、若击球高度低于 , 无论球的初速度多大,球都不可能落在对方界内 -
13、如图所示,吊篮A、物体B、物体C的质量分别为m、2m、3m,B和C分别固定在竖直弹簧两端,弹簧的质量不计。整个系统在轻绳悬挂下处于静止状态,重力加速度为g,现将悬挂吊篮的轻绳剪断,在轻绳刚断的瞬间( )
 A、吊篮A的加速度大小为g B、物体B的加速度大小为1.5g C、物体C的加速度大小为1.5g D、A、C间的弹力大小为mg
A、吊篮A的加速度大小为g B、物体B的加速度大小为1.5g C、物体C的加速度大小为1.5g D、A、C间的弹力大小为mg -
14、某人站在力的传感器(连着计算机)上完成下蹲、起立动作,计算机屏幕上显示出力的传感器示数F随时间t变化的情况如图所示,g取10m/s2。下列说法正确的是( )
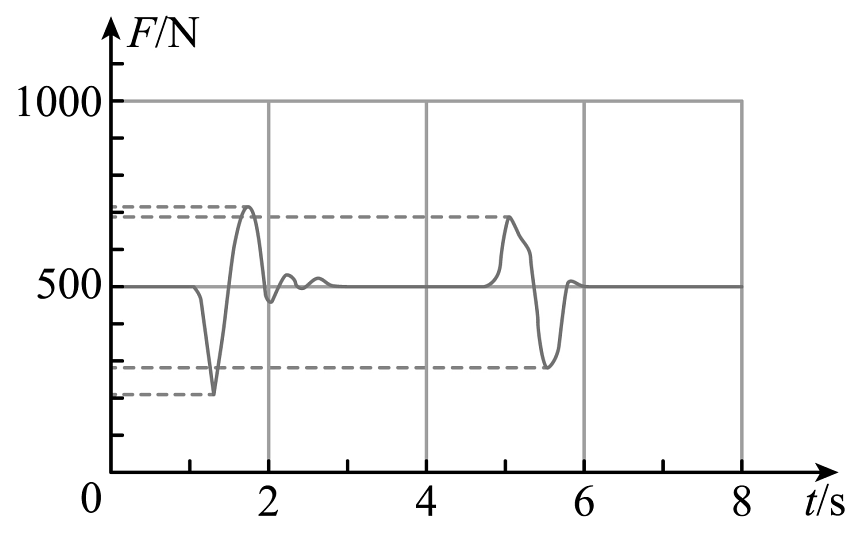 A、该人下蹲时间约为0.5s B、下蹲过程该人一直处于失重状态 C、起立过程该人一直处于超重状态 D、该人下蹲过程的最大加速度约为6m/s2
A、该人下蹲时间约为0.5s B、下蹲过程该人一直处于失重状态 C、起立过程该人一直处于超重状态 D、该人下蹲过程的最大加速度约为6m/s2 -
15、“笛音雷”是某些地区春节期间常放的一种鞭炮,其着火后一段时间内的速度—时间图像如图所示(取竖直向上为正方向),其中时刻为“笛音雷”起飞时刻、DE段是斜率大小为重力加速度g的直线。不计空气阻力,则关于“笛音雷”的运动,下列说法正确的是( )
 A、“笛音雷”在t2时刻上升至最高点 B、t3~t4时间内“笛音雷”做自由落体运动 C、t0~t1时间内“笛音雷”的平均速度小于 D、t1~t2时间内“笛音雷”的加速度先减小后增大
A、“笛音雷”在t2时刻上升至最高点 B、t3~t4时间内“笛音雷”做自由落体运动 C、t0~t1时间内“笛音雷”的平均速度小于 D、t1~t2时间内“笛音雷”的加速度先减小后增大 -
16、具有“主动刹车系统”的汽车与正前方静止障碍物之间的距离小于安全距离时,会立即开始主动刹车,车主可根据需要设置安全距离。某车的安全距离为15m,若汽车正以54km/h的速度在路面上行驶,遇紧急情况主动刹车后做匀减速直线运动,加速度大小为6m/s2 , 下列说法正确的是( )A、汽车刹车时间为3s B、汽车不能安全停下 C、汽车开始“主动刹车”后第1s末的速度为10m/s D、汽车开始“主动刹车”后第3s内的平均速度为1.5m/s
-
17、如图所示,在质量为的物块甲上系着两条细绳,其中长的细绳另一端连着轻质圆环,圆环套在水平棒上可以滑动,圆环与棒间的动摩擦因数。另一细绳跨过光滑定滑轮与重力为的物块乙相连,定滑轮固定在距离圆环的地方,系统处于静止状态,与棒的夹角为 , 两绳夹角为。当时,圆环恰好开始滑动。最大静摩擦力等于滑动摩擦力, , , 。求:
 (1)、绳与棒间的夹角;(2)、物块甲的质量。
(1)、绳与棒间的夹角;(2)、物块甲的质量。 -
18、如图,整个空间有场强大小为的匀强电场,方向水平向右。为竖直面的绝缘光滑轨道,其中部分是水平轨道,部分是半径为的四分之一圆弧,两段轨道相切于点。P为水平轨道上的一点,且 , 把一质量、带电荷量小球从P点由静止释放,小球将在轨道内运动,重力加速度 , 求:
(1)小球到达点时的速率;
(2)小球从点到点的过程中动能的最大值;
(3)小球离开C点后再次到达同一水平高度时与P点的距离。

-
19、一个右端开口左端封闭的U形玻璃管中装有水银,左侧封有一定质量的空气,如图所示,已知,空气柱长是40cm,两侧水银面高度差56cm,若左侧距管顶66cm处的k点处突然断开,断开处上方水银能否流出?这时左侧上方封闭气柱将变为多高?(设大气压强为1.013×105Pa)

-
20、轮固定在同一转轴上,轮用皮带连接且不打滑。边缘点A、B,已知轮的半径比 , 当转轴匀速转动时,则( )
 A、A、B线速度之比为 B、A、B角速度之比为 C、A、B加速度之比为 D、A、B周期之比为
A、A、B线速度之比为 B、A、B角速度之比为 C、A、B加速度之比为 D、A、B周期之比为