相关试卷
-
1、当圆截直线所得的弦长最短时,实数( )A、-1 B、 C、1 D、
-
2、已知 , 两直线 , 若 , 则的最小值为( )A、12 B、20 C、26 D、32
-
3、已知复数满足 , 则( )A、 B、 C、 D、
-
4、已知平面 , , 直线 , 且 , 则“”是“∥”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
5、在空间直角坐标系中,点关于轴的对称点的坐标为( )A、 B、 C、 D、
-
6、如图,已知圆的方程为 , 直线与圆交于 , (在上方),直线与圆交于 , (在上方).原点在圆内.设交轴于点 , 交轴于点 .
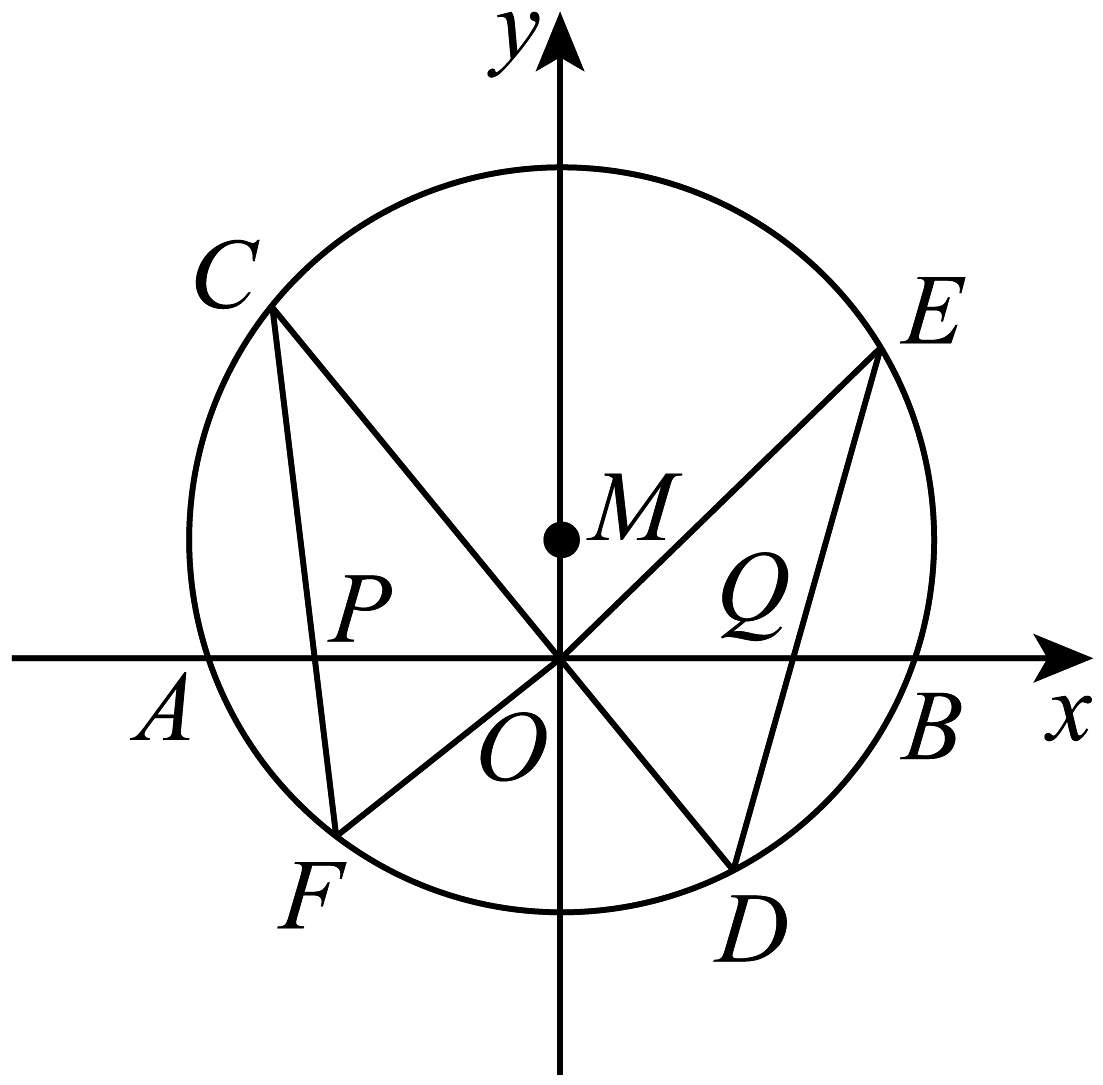 (1)、当 , , , 时,分别求线段和的长度;(2)、①求证:;
(1)、当 , , , 时,分别求线段和的长度;(2)、①求证:;②猜想和的大小关系,并证明.
-
7、已知椭圆的左、右焦点分别为 , 若斜率为的直线过椭圆的焦点以及点.点P是椭圆上与左、右顶点不重合的点,且的面积最大值.(1)、求椭圆的方程;(2)、过点的直线交椭圆于点、 , 且满足(为坐标原点),求直线的方程.
-
8、如图,平面ABCD, , , , , ,
 (1)、求直线CE与平面BDE所成角的正弦值;(2)、求平面BDE与平面BDF的夹角.
(1)、求直线CE与平面BDE所成角的正弦值;(2)、求平面BDE与平面BDF的夹角. -
9、已知 , , . 求:(1)、BC边上的中线所在的直线方程;(2)、AB边垂直平分线方程;
-
10、已知椭圆的长轴长为4,离心率为.若分别是椭圆的上,下顶点,分别为椭圆的上,下焦点,为椭圆上任意一点,且 , 则的面积为.
-
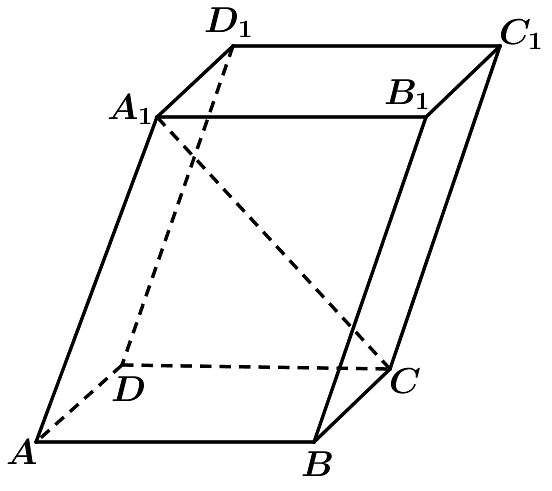
11、如图,在平行六面体中,底面是边长为1的正方形,若 , 且 , 则的长为 .
-
12、已知点到直线l:的距离为d,则d的可能取值是( )A、0 B、1 C、 D、4
-
13、古希腊著名数学家阿波罗尼斯发现:已知平面内两个定点及动点 , 若且 , 则点的轨迹是圆. 后来人们将这个圆以他的名字命名,称为阿波罗尼斯圆(简称“阿氏圆”).在平面直角坐标系中,已知 , 直线 , 直线 , 若为的交点,则的最小值为( )A、 B、 C、 D、
-
14、将边长为1的正方形沿对角线翻折,使得二面角的平面角的大小为 , 若点 , 分别是线段和上的动点,则的取值范围为( )A、 B、 C、 D、
-
15、已知圆和圆恰有三条公共切线,则的最小值为( )A、6 B、36 C、10 D、
-
16、已知椭圆的左、右焦点分别为 , 过点作直线与椭圆交于两点,设 , 若内切圆的面积为 , 则( )A、 B、 C、 D、
-
17、如图,四棱锥的底面是矩形,设 , , , 是棱上一点,且 , 则( )
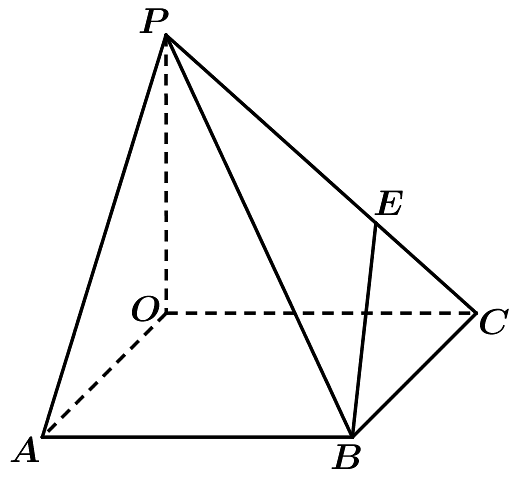 A、 B、 C、 D、
A、 B、 C、 D、 -
18、已知两个非零向量它们平行的充要条件是( )A、 B、 C、 D、存在非零实数k,使
-
19、直线: , 直线: , 则直线是的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
-
20、已知直线l经过点和 两点,则直线l的倾斜角是( )A、 B、45° C、60° D、120°