相关试卷
-
1、已知()在处取得极值.(1)、求实数的值;(2)、求的单调区间;(3)、求在区间上的最大值和最小值.
-
2、已知点 , 点Р是圆C:上的任意一点,线段PA的垂直平分线与直线CP交于点E.(1)、求点E的轨迹方程;(2)、若直线与点E的轨迹有两个不同的交点F和Q,且原点О总在以FQ为直径的圆的内部,求实数m的取值范围.
-
3、已知函数 , 其导函数为 , 则的值为( )A、1 B、2 C、3 D、4
-
4、函数的单调递增区间是.
-
5、对于任意两个正数 , 记曲线与直线 , , 轴围成的曲边梯形的面积为 , 并约定和 , 德国数学家莱布尼茨(Leibniz)最早发现.关于 , 下列说法正确的是( )A、 B、 C、 D、
-
6、如图是函数的图象,则下列说法正确的是( )
 A、在上单调递减 B、在上单调递增 C、在区间上的最大值为3,最小值为 D、在上有最大值3,有最小值
A、在上单调递减 B、在上单调递增 C、在区间上的最大值为3,最小值为 D、在上有最大值3,有最小值 -
7、定义:在一个有穷数列的每相邻两项之间插入这两项的和,形成新的数列,我们把这样的操作称为该数列的一次“和扩充”,例如:数列经过第一次“和扩充”后得到数列;第二次“和扩充”后得到数列 . 设数列经过次“和扩充”后得到的数列的项数为 , 所有项的和为 .(1)、若 , 求;(2)、求不等式的解集;(3)、是否存在数列 , 使得数列为等比数列?请说明理由.
-
8、已知双曲线的焦距为8,右焦点为 , 直线与双曲线在一、三象限的交点分别为 , 且 .(1)、求双曲线的方程及的面积;(2)、直线与双曲线交于两点,若直线与轴分别交于点 , 且 . 证明:为定值.
-
9、为增加学生对于篮球运动的兴趣,学校举办趣味投篮比赛,第一轮比赛的规则为:选手需要在距离罚球线1米,2米,3米的三个位置分别投篮一次.在三个位置均投进得10分;在处投进,且在两处至少有一处未投进得7分;其余情况(包括三处均不投进)保底得4分.已知小王在三处的投篮命中率分别为 , 且在三处的投篮相互独立.(1)、设为小王同学在第一轮比赛的得分,求的分布列和期望;(2)、若第二轮比赛中设置两种参赛方法.方法1:按第一轮比赛规则进行比赛;方法2:选手可以选择在处缩短投篮距离0.5米,但得分会减少分.选手可以任选一种规则参加比赛.若小王在处缩短投篮距离0.5米后,投篮命中率会增加 . 请你根据统计知识,帮助小王同学选择采用哪种方法参加比赛更好.
-
10、在三棱柱中,侧面平面 , , 侧面为菱形,且为中点.
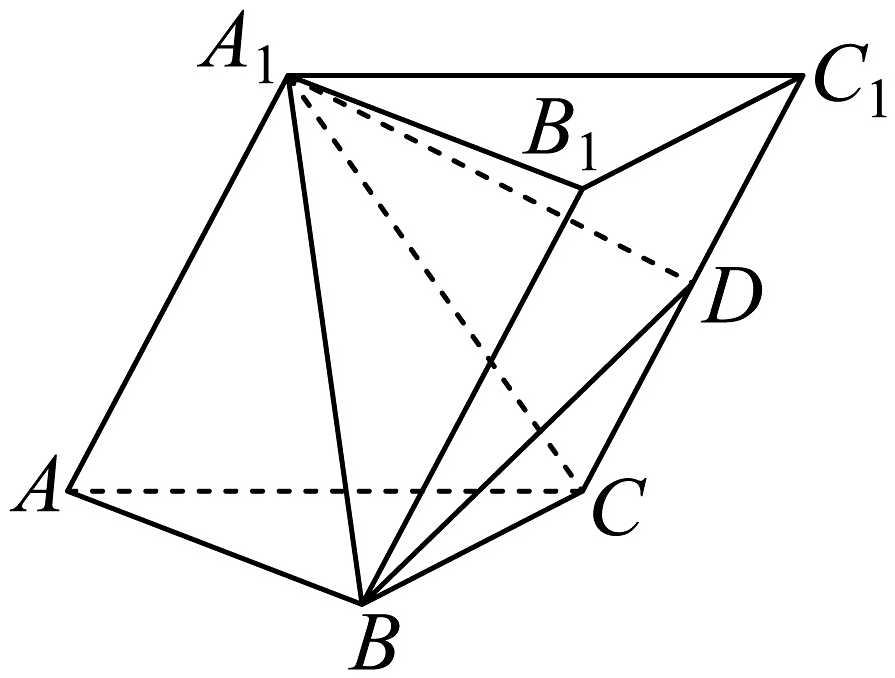 (1)、证明:平面;(2)、求二面角的余弦值.
(1)、证明:平面;(2)、求二面角的余弦值. -
11、已知函数的图象在点处的切线过点 .(1)、求实数的值;(2)、求的单调区间和极值.
-
12、已知抛物线的焦点为 , 直线交抛物线于两点,为抛物线的准线与轴的交点,直线分别交抛物线于两点(点异于点 , ),为坐标原点,则实数的取值范围为; .
-
13、已知 , 若 , 使成立,则 .
-
14、春节期间,小明一家3口、姑姑一家3口和爷爷,奶奶围坐圆桌聚餐,则在爷爷、奶奶相邻的前提下,小明一家3口均不相邻的概率为 .
-
15、如图所示,四面体的各棱长均为分别为棱的中点,为棱上异于顶点的点,则以下结论正确的为( )
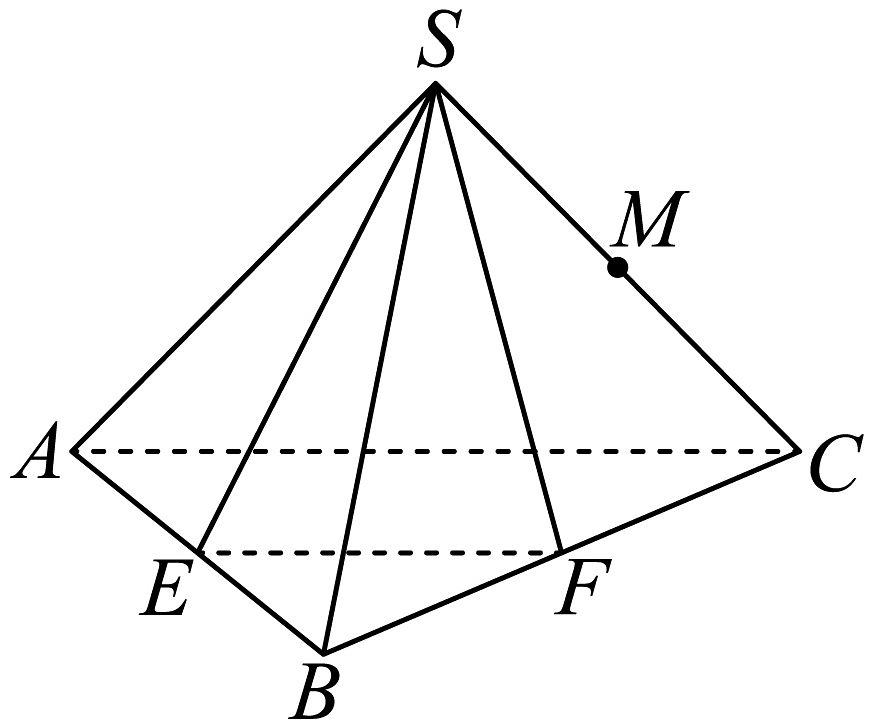 A、 B、直线与所成角的余弦值为 C、四面体的外接球体积为 D、平面截四面体所得的截面图形的周长最小值为8
A、 B、直线与所成角的余弦值为 C、四面体的外接球体积为 D、平面截四面体所得的截面图形的周长最小值为8 -
16、下列命题为真命题的是( )A、若 , 则 B、若 , 则 C、若的展开式中的常数项为60,则 D、若随机变量的方差 , 则
-
17、已知 , 若成立,则实数的最小值为( )A、2 B、3 C、4 D、5
-
18、设为数列的前项和, , 则“”是“数列是以为公比的等比数列”的( )A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件
-
19、已知非空集合 , 若 , 则实数的取值范围为( )A、 B、 C、 D、
-
20、已知定义在上的函数满足为偶函数,为奇函数,当时, , 则下列说法正确的是( )A、 B、函数为周期函数 C、函数为上的偶函数 D、