相关试卷
-
1、已知甲、乙两组数据已整理成如图所示的茎叶图,则甲组数据的中位数是 , 乙组数据的25%分位数是 .

-
2、若 , 则为 .
-
3、在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”的可能性最大的线路是( )
 A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Q
A、P→A→Q B、P→B→Q C、P→C→Q D、P→D→Q -
4、大多数居民在住宅区都会注意噪音问题.记为实际声压,通常我们用声压级(单位:分贝)来定义声音的强弱,声压级与声压存在近似函数关系: , 其中为常数,且常数为听觉下限阈值.若在某栋居民楼内,测得甲穿硬底鞋走路的声压为穿软底鞋走路的声压的倍,且穿硬底鞋走路的声压级为分贝,恰为穿软底鞋走路的声压级的倍.若住宅区夜间声压级超过分贝即扰民,该住宅区夜间不扰民情况下的声压为 , 则( )A、 , B、 , C、 , D、 ,
-
5、已知 , , , , 则( )A、 B、 C、 D、
-
6、在平行四边形ABCD中,设对角线AC与BD相交于点O,则( )A、 B、 C、 D、
-
7、已知 , 则“”是“”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
8、已知一组数的平均数 , 方差 , 则数据的平均数和方差分别是( )A、3,2 B、3,4 C、2,4 D、2,2
-
9、从装有两个红球和两个白球的口袋内任取两个球,则下列事件是对立事件的是( )A、“都是白球”与“至少有一个白球” B、“恰有一个白球”与“都是红球” C、“都是白球”与“都是红球” D、“至少有一个白球”与“都是红球”
-
10、下列函数中,既是偶函数又在区间上单调递增的是( )A、 B、 C、 D、
-
11、已知空间向量 , , , 若 , 则 .
-
12、为了研究学生每天整理数学错题的情况,某课题组在某市中学生中随机抽取了100名学生调查了他们期中考试的数学成绩和平时整理数学错题情况,并绘制了下列两个统计图表,图1为学生期中考试数学成绩的频率分布直方图,图2为学生一个星期内整理数学错题天数的扇形图.若本次数学成绩在110分及以上视为优秀,将一个星期有4天及以上整理数学错题视为“经常整理”,少于4天视为“不经常整理”. 已知数学成绩优秀的学生中,经常整理错题的学生占.
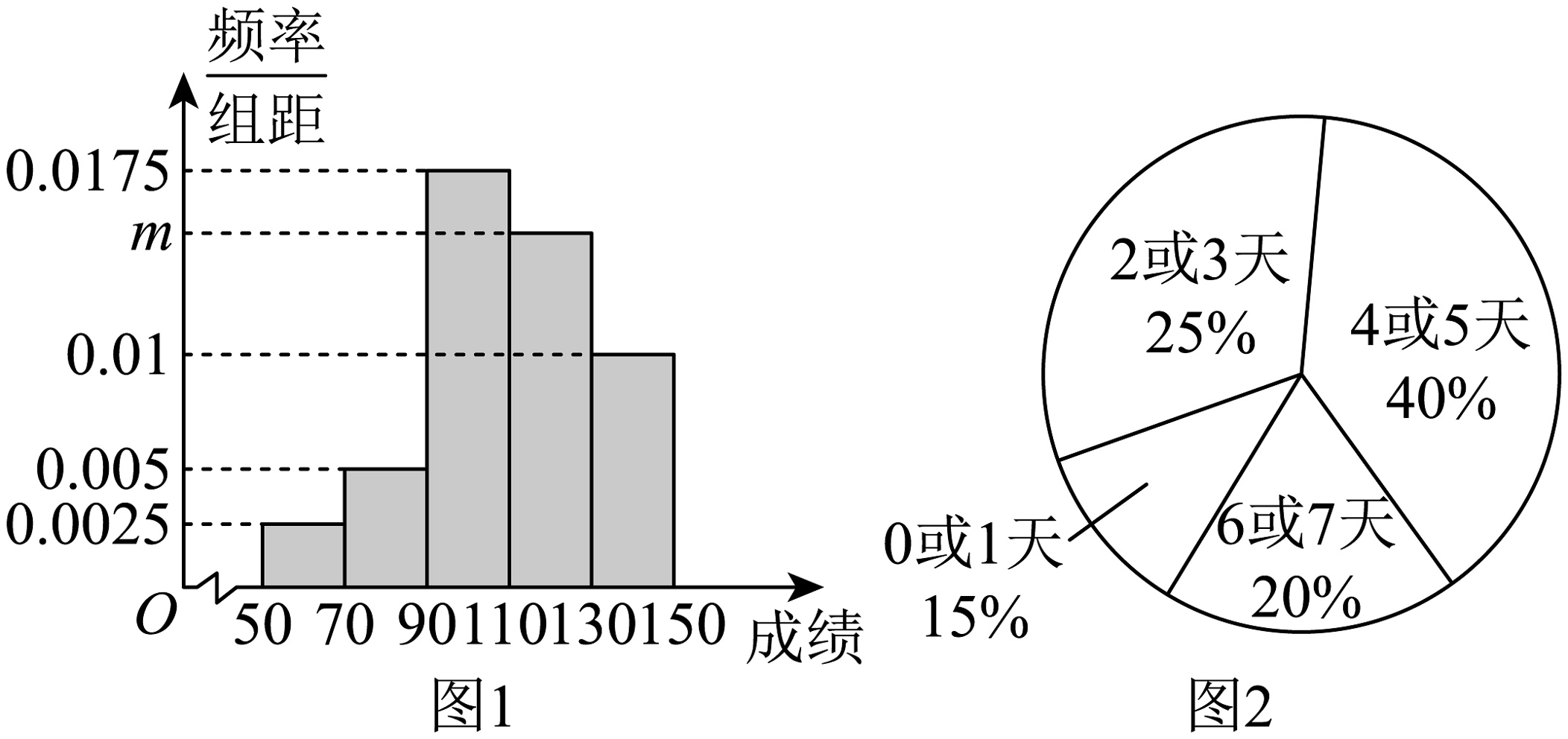
数学成绩优秀
数学成绩不优秀
合计
经常整理
不经常整理
合计
(1)、求图1中的值;(2)、根据图1、图2中的数据,补全上方列联表,并根据小概率值的独立性检验,分析数学成绩优秀与经常整理数学错题是否有关?附:
-
13、已知函数 , (注:是自然对数的底数).(1)、当时,求曲线在点处的切线方程;(2)、若只有一个极值点,求实数a的取值范围.
-
14、已知件产品中有件合格品和件次品,现从这件产品中分别采用有放回和不放回的方式随机抽取件,设采用有放回的方式抽取的件产品中合格品数为 , 采用无放回的方式抽取的件产品中合格品数为 .(1)、求;(2)、求的分布列及数学期望;(3)、比较数学期望与的大小.
-
15、已知集合 , 且满足 , , 求实数 , 的值.
-
16、已知函数 , 则不等式的解集为.
-
17、如图,二面角的大小为 , 其棱l上有两个点 , 线段与分别在这个二面角的两个面内,并且都垂直于棱l.若则两点间的距离为 .
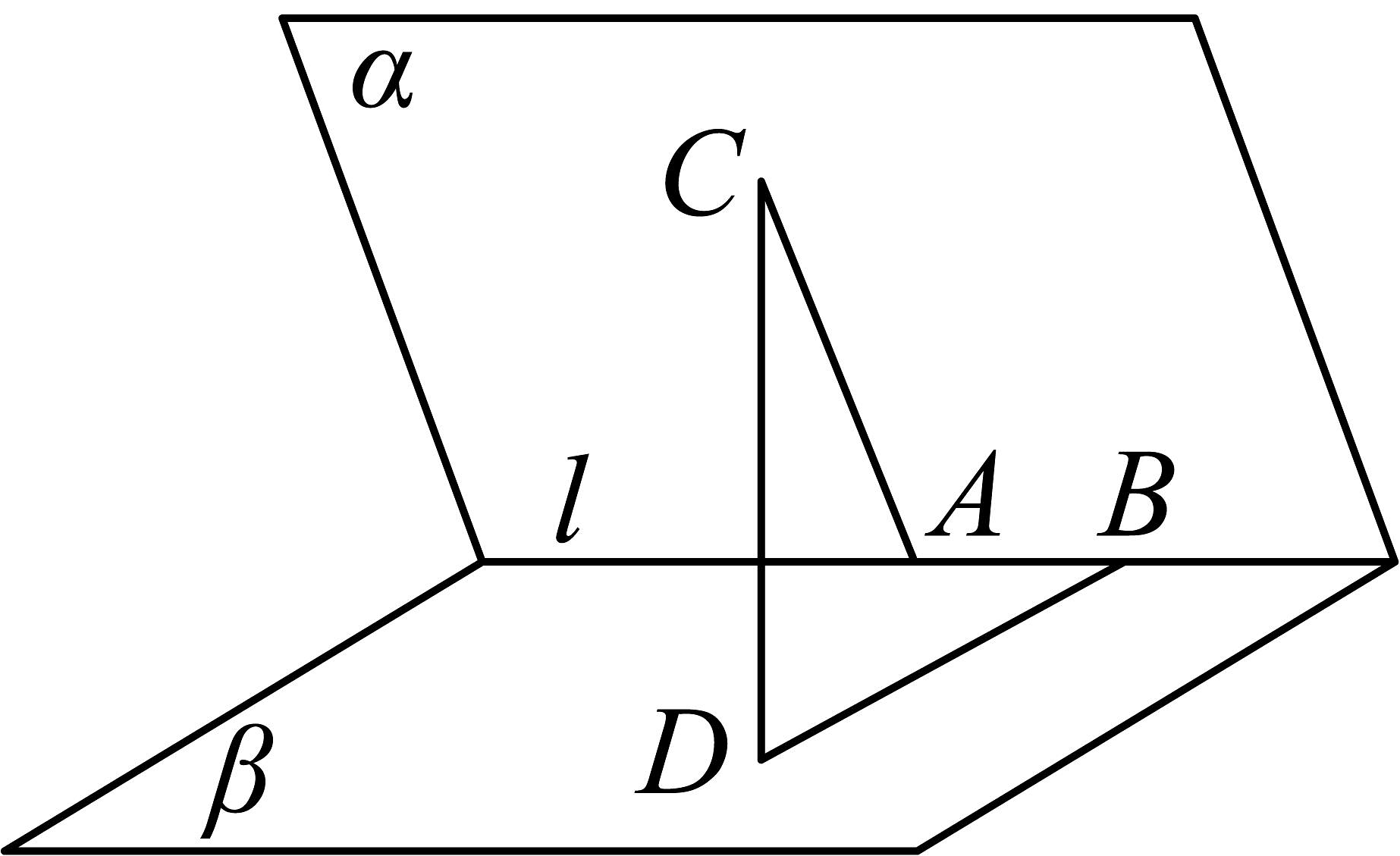
-
18、若 , 且 , 则的最大值为.
-
19、我国古代数学名著《九章算术》中将“底面为直角三角形且侧棱垂直于底面的三棱柱”称为“堑堵”.现有一如图所示的“暂堵” , 其中 , 若 , 则( )
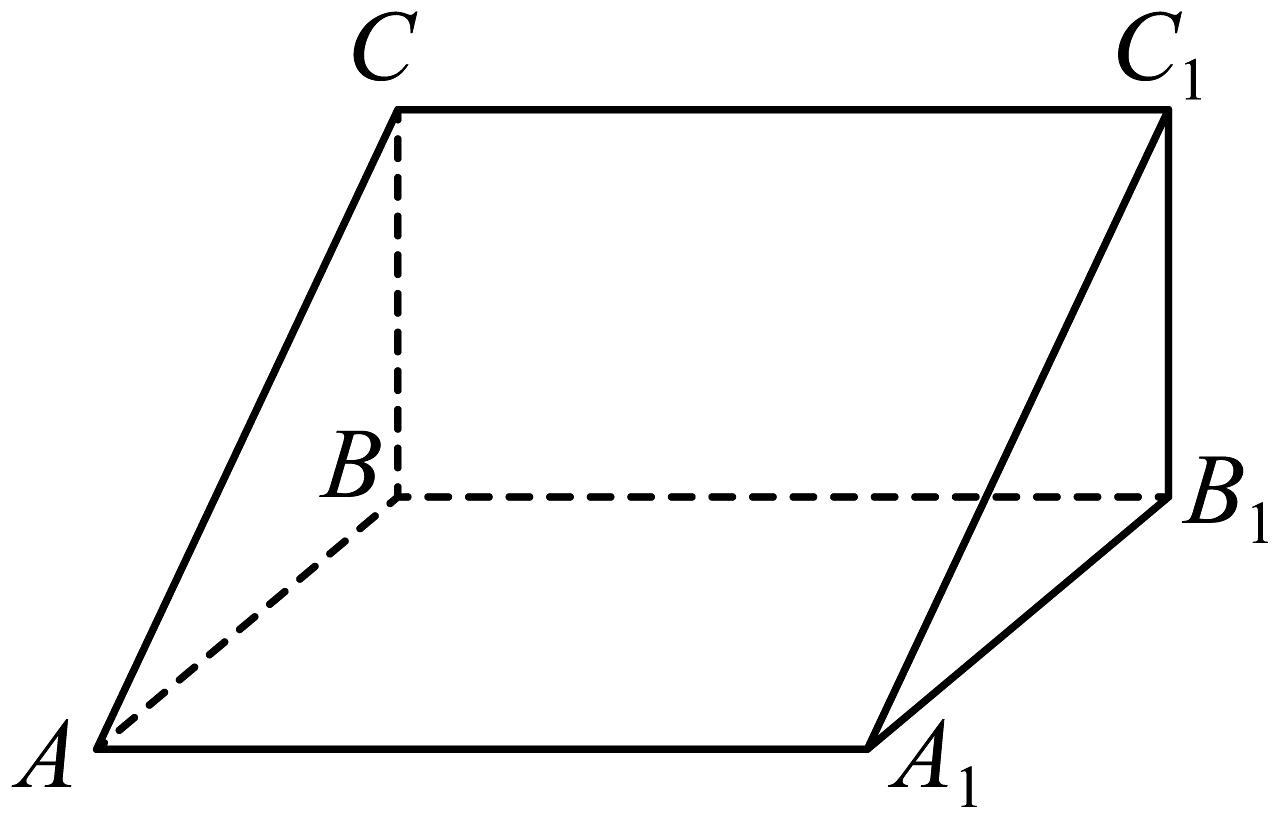 A、该“堑堵”的体积为2 B、该“堑堵”外接球的表面积为 C、若点P在该“堑堵”上运动,则的最大值为 D、该“堑堵”上,与平面所成角的正切值为
A、该“堑堵”的体积为2 B、该“堑堵”外接球的表面积为 C、若点P在该“堑堵”上运动,则的最大值为 D、该“堑堵”上,与平面所成角的正切值为 -
20、下列四个命题中假命题是( )A、 , B、 , C、 , 使 D、 ,