相关试卷
-
1、已知集合 , 集合 , 则( )A、 B、 C、 D、
-
2、已知角的顶点与原点重合,始边与x轴的非负半轴重合,终边在直线上.
(1)求的值;
(2)若 , 且 , 求的值.
-
3、已知函数的图象的两相邻零点之间的距离小于 , 为函数的极大值点,且 , 则实数的最小值为.
-
4、 .
-
5、已知函数 , 以下说法正确的有( )A、若的定义域是 , 则 B、若的定义域是 , 则 C、若恒成立,则 D、若 , 则的值域不可能是
-
6、已知 , , 且 , 下列结论中正确的是( )A、的最大值是 B、的最小值是 C、的最小值是8 D、的最小值是
-
7、设函数在R上存在导数 , 对任意的 , 有 , 且时, . 若 , 则实数a的取值范围为( )A、 B、 C、 D、
-
8、已知函数 , 则( )A、在区间上单调递增 B、在区间上单调递减 C、在区间上单调递增 D、在区间上单调递减
-
9、若函数的定义域为 , 则实数的取值范围是( )A、 B、 C、 D、
-
10、设集合 , 则( )A、 B、 C、 D、
-
11、如图,在长方体中, , 分别为 , 的中点, , 分别为 , 的中点,则下列说法正确的是( )
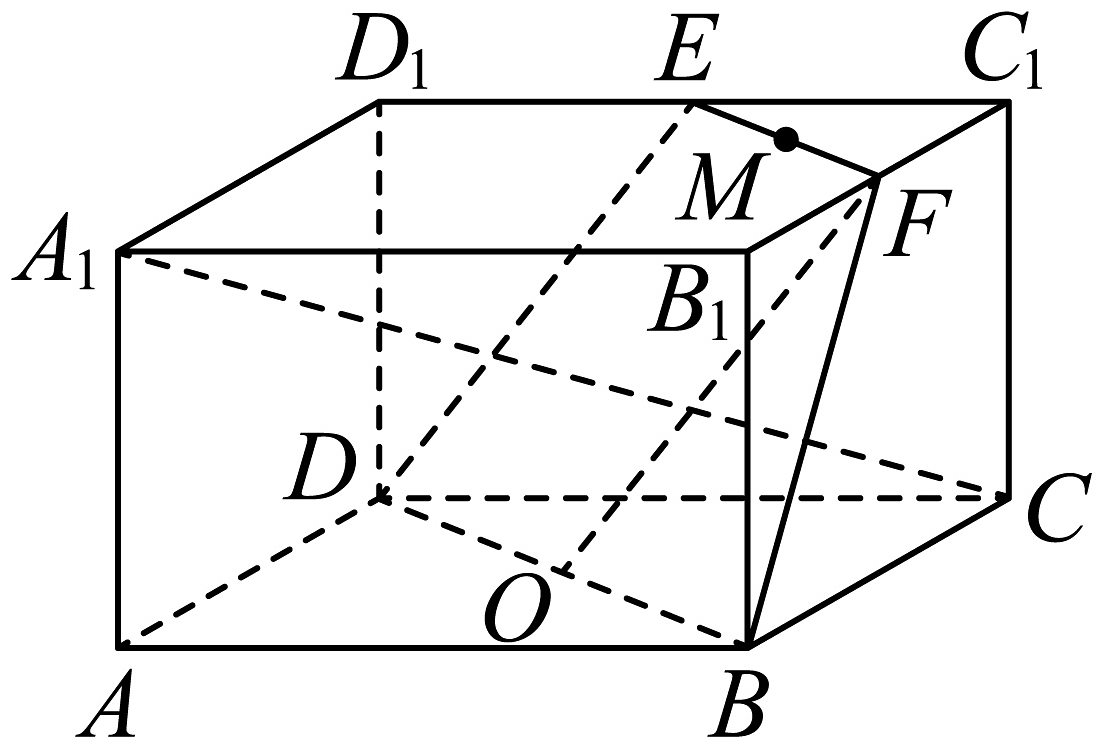 A、四点 , , , 在同一平面内 B、三条直线 , , 有公共点 C、直线与直线不是异面直线 D、直线上存在点使 , , 三点共线
A、四点 , , , 在同一平面内 B、三条直线 , , 有公共点 C、直线与直线不是异面直线 D、直线上存在点使 , , 三点共线 -
12、若函数为定义域上单调函数,且存在区间(其中),使得当时,的取值范围恰为 , 则称函数是D上的正函数,区间叫做等域区间.(1)、是否存在实数m,使得函数是上的正函数?若存在,请求出实数m的取值范围;若不存在,请说明理由.(2)、若 , 且不等式的解集恰为 , 求函数的解析式.并判断是否为函数的等域区间.
-
13、已知函数.(1)、求函数在上的单调递增区间;(2)、在中,分别为角的对边, , , 求面积的最大值.
-
14、的展开式中常数项为 .
-
15、若 , , , 则的最小值为 .
-
16、已知函数是定义在上的奇函数,且满足 , 当时, , 则下列说法正确的是( )A、 B、函数的图像关于直线对称 C、定义在上的函数满足 , 若曲线与恰有2025个交点 , 则 D、当实数时,关于的方程恰有四个不同的实数根
-
17、已知随机变量服从正态分布,即 , 则( )A、 B、 C、 D、
-
18、已知 , , 若 , 则实数( )A、 B、2 C、 D、1
-
19、已知复数满足 , 则( )A、 B、2 C、 D、
-
20、已知全集 , 集合 , 为素数 , 则( )A、 B、 C、 D、