相关试卷
-
1、某学校为了调查学生在一周生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在[50,60)内的学生有60人,则下列说法正确的是( )
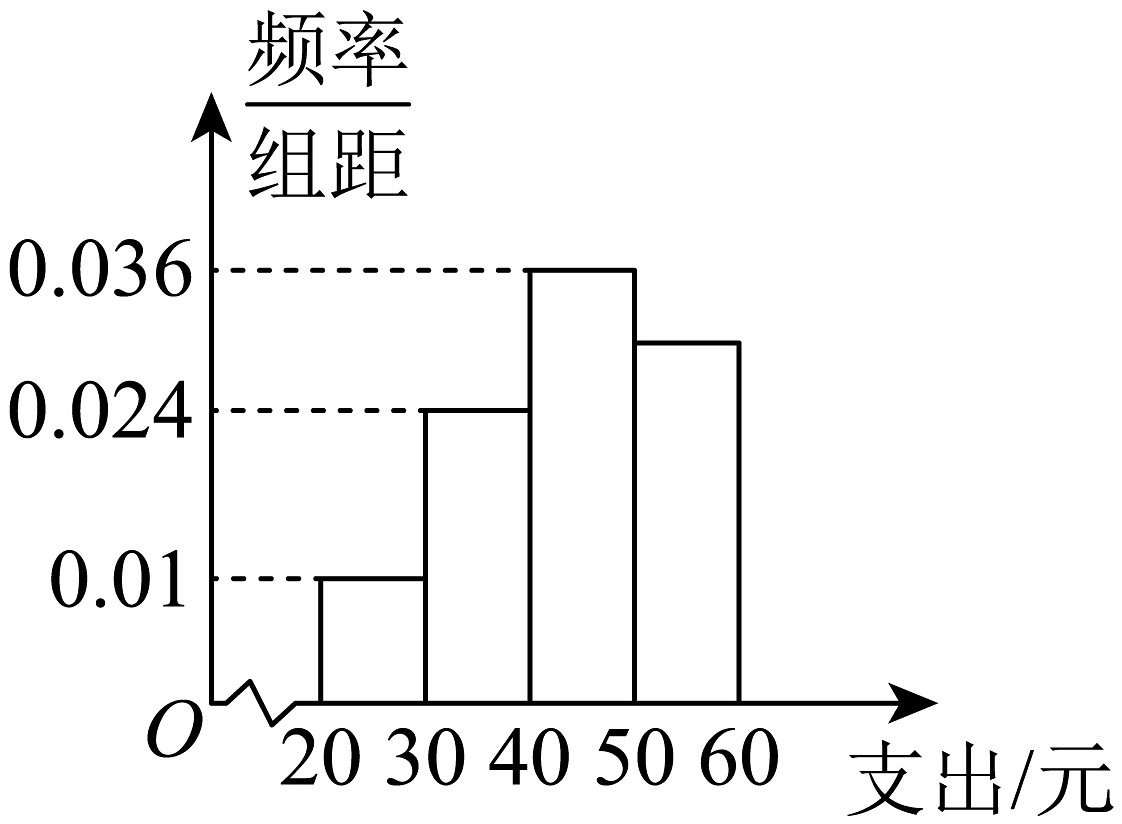 A、样本中支出在[50,60)内的频率为0.03 B、样本中支出不少于40元的人数为132 C、n的值为200 D、若该校有2000名学生,则估计有600人支出在[50,60)内
A、样本中支出在[50,60)内的频率为0.03 B、样本中支出不少于40元的人数为132 C、n的值为200 D、若该校有2000名学生,则估计有600人支出在[50,60)内 -
2、在中,若 , 则的形状是A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形
-
3、已知函数 , 若对于任意 , 恒成立,则实数的取值范围为( )A、 B、 C、 D、
-
4、若函数的值域为 , 则函数的值域为( )A、 B、 C、 D、
-
5、牛奶保鲜时间因储藏温度的不同而不同.假定保鲜时间与储藏温度的关系为(、为常量).若牛奶在0的冰箱中,保鲜时间约是100h,在5的冰箱中,保鲜时间约是80h,那么在10中的保鲜时间约是( )A、49h B、56h C、64h D、76h
-
6、设复数z满足 , 则( )A、1 B、2 C、 D、
-
7、下列四组函数中与是同一函数的是( )A、 B、 C、 D、
-
8、设等比数列的前项和为 , 前项的乘积为 . 若 , 则( )A、无最小值,无最大值 B、有最小值,无最大值 C、无最小值,有最大值 D、有最小值,有最大值
-
9、如图,在直三棱柱中,侧面是正方形, , 分别是棱的中点,且 .
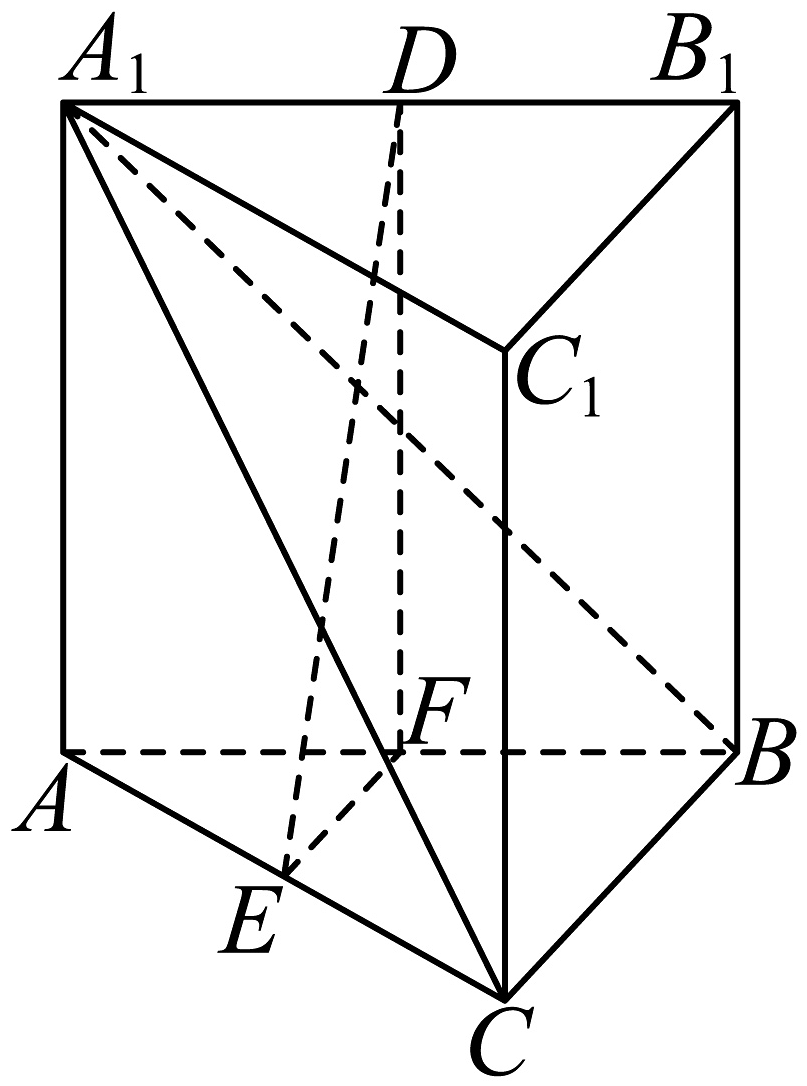 (1)、若 , 证明:平面;(2)、当平面与平面夹角的余弦值最大时,求的值.
(1)、若 , 证明:平面;(2)、当平面与平面夹角的余弦值最大时,求的值. -
10、已知函数.(1)、求函数的最小正周期及单调递增区间;(2)、将函数的图象上所有点向上平移个单位得到曲线 , 再将上的各点纵坐标变为原来的倍(横坐标不变),得到函数的图象.若 , , 不等式成立,求实数的取值范围.
-
11、已知平面向量 , .(1)、若 , 求的值;(2)、若 , 求 .
-
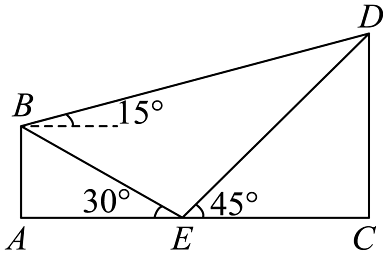
12、香霏楼是荣昌昌州故里景区的标志性建筑之一,也是荣昌历史文化的重要象征.某同学为测量香霏楼的高度 , 在香霏楼的正西方向找到一座建筑物 , 高约为15m,在地面上点E处(A,C,E三点共线)测得建筑物顶部B,香霏楼顶部D的仰角分别为和 , 在B处测得塔顶部D的仰角为 , 则香霏楼的顶部与地面的距离约为 m..

-
13、计算 .
-
14、在△ABC中,角A,B,C的对边分别是a,b,c,且满足 , 则( )A、 B、若b=4,则△ABC的周长的最大值为 C、若D为AC的中点,且BD=2,则△ABC的面积的最大值为 D、若角B的平分线BD与边AC相交于点D,且 , 则a+4c的最小值为9
-
15、已知的定义域为 , 值域为 , 则( )A、若 , 则 B、对任意 , 使得 C、对任意的图象恒过一定点 D、若在上单调递减,则的取值范围是
-
16、下列说法正确的是( )A、某人掷骰子1次,“掷出5”与“掷出6”是互斥事件 B、甲、乙、丙三种个体按的比例分层抽样,如果抽取的甲个体数为3,则抽取的丙个体数为9 C、数据 , , , , , , , 的分位数是8 D、数据 , , , …,的方差为 , 则数据 , , , …,的方差为
-
17、在中, , 若以m为参数的不等式恒成立,则m的取值范围是( )A、 B、 C、 D、
-
18、在菱形中, , 将折起到的位置,若三棱锥的外接球的体积为 , 则二面角的正弦值为( )A、 B、 C、 D、
-
19、若函数( , , )的图象上有两个相邻顶点为 , .将的图象沿x轴向左平移1个单位,再沿y轴向上平移个单位后得 , 则为( )A、 B、 C、 D、
-
20、一个正四棱台的上底面边长为1,下底面边长为2,若一个球与该正四棱台的各面均相切,则该球的体积为( )A、 B、 C、 D、