相关试卷
-
1、已知数列的前项和为 , 且(1)、求数列的通项公式;(2)、令 , 求数列的前项和
-
2、甲、乙两台机床生产同种产品,产品按质量分为一级品和二级品,为了比较两台机床产品的质量,分别用两台机床各生产了200件产品,产品的质量情况统计如下表.
机床
品级
合计
一级品
二级品
甲机床
150
50
200
乙机床
120
80
200
合计
270
130
400
(1)、甲机床、乙机床生产的产品中一级品的频率分别是多少?(2)、依据小概率值的独立性检验,分析甲机床的产品质量是否与乙机床的产品质量有差异.附:χ2=.
α
0.050
0.010
0.001
xα
3.841
6.635
10.828
-
3、已知函数 , 若在处的切线斜率为 , 则;若恒成立,则的取值范围为
-
4、若从2025的所有正约数中任取一个数,则这个数是一个完全平方数的概率为 .
-
5、设正整数 , 其中 , 记为上述表示中为1的个数.例如: , 所以 . 已知集合 , 下列说法正确的是( )A、 B、对任意的 , 有 C、若 , 则使成立的的取值个数为 D、
-
6、已知离数型随机变量X的分布列如下表所示:
X
0
1
2
P
下列说法正确的是( )
A、 B、 C、 D、 -
7、下列说法正确的是( )A、利用进行独立性检验时,的值越大,说明有更大的把握认为两个分类变量独立 B、在残差图中,残差点分布的带状区域的宽度越窄,其模型拟合效果越好 C、样本相关系数r的大小可以反映成对样本数据之间线性相关的程度,当r越小,成对样本数据的线性相关程度越弱 D、用决定系数来比较两个模型的拟合效果.越大,表示残差平方和越小,即模型的拟合效果越好
-
8、下列四组数据中,方差最小的为( )A、31,22,39 B、30,46,25 C、40,18,30 D、37,42,33
-
9、设函数 , 则曲线在点处的切线与两坐标轴所围成的三角形的面积为( )A、 B、 C、 D、
-
10、下列命题错误的是( )A、有一组数据为、、、、、、、 , 则它们的第百分位数为 B、线性回归直线一定经过样本点的中心 C、设 , 且 , 则 D、随机变量 , 若 , , 则
-
11、下列说法正确的是( )A、中国灯笼又统称为灯彩,主要有宫灯、纱灯、吊灯等种类,现有4名学生,每人从宫灯、纱灯、吊灯中选购1种,则不同的选购方式有24种 B、从A村去B村的道路有3条,从B村去C村的道路有5条,则从A村经过B村去C村不同的路线的条数为8 C、一个两层书架,分别放置语文类读物4本,数学类读物5本,每本读物各不相同,从中取出1本,则不同的取法共有20种 D、从1,2,3,4,5五个数字中任选3个数字,可组成无重复数字的三位数的个数为60
-
12、记为等差数列的前n项和,已知 , , 则( )A、 B、 C、 D、
-
13、下列图中,线性相关性系数最大的是( )A、
 B、
B、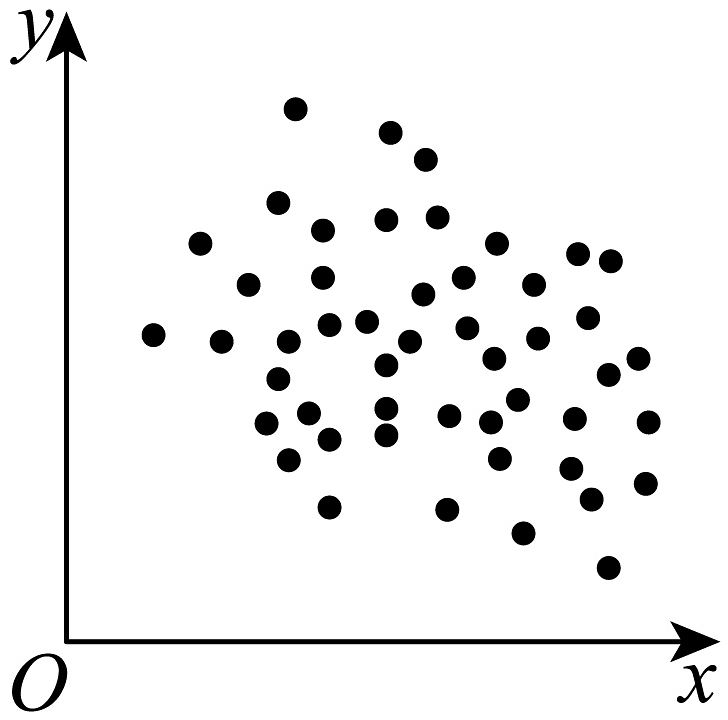 C、
C、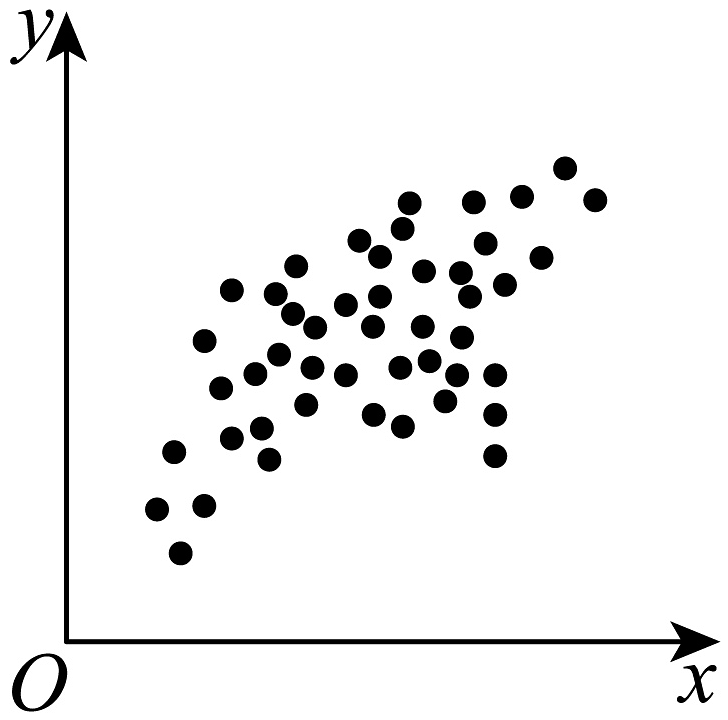 D、
D、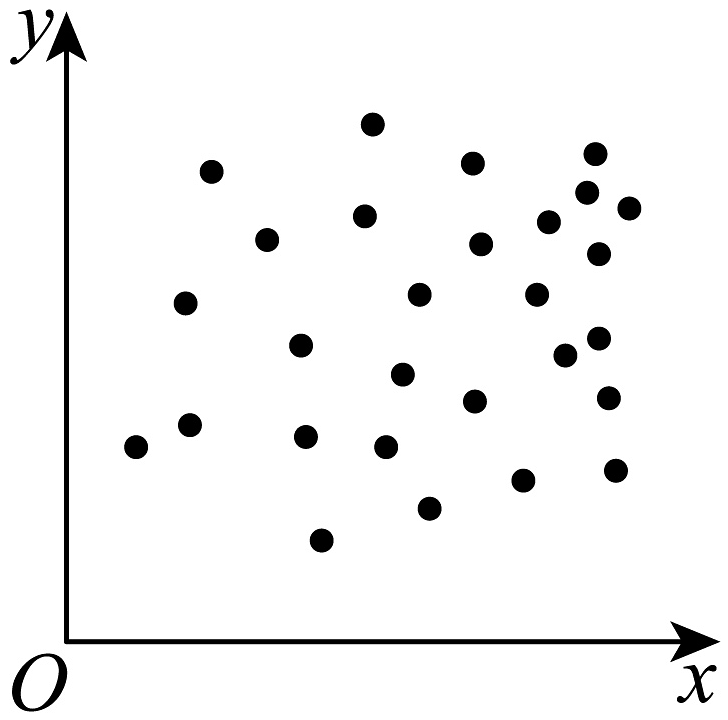
-
14、计算的值是( )A、41 B、61 C、62 D、82
-
15、如图1,在矩形ABCD中, , , M是边BC上的一点,将沿着AM折起,使点B到达点P的位置.
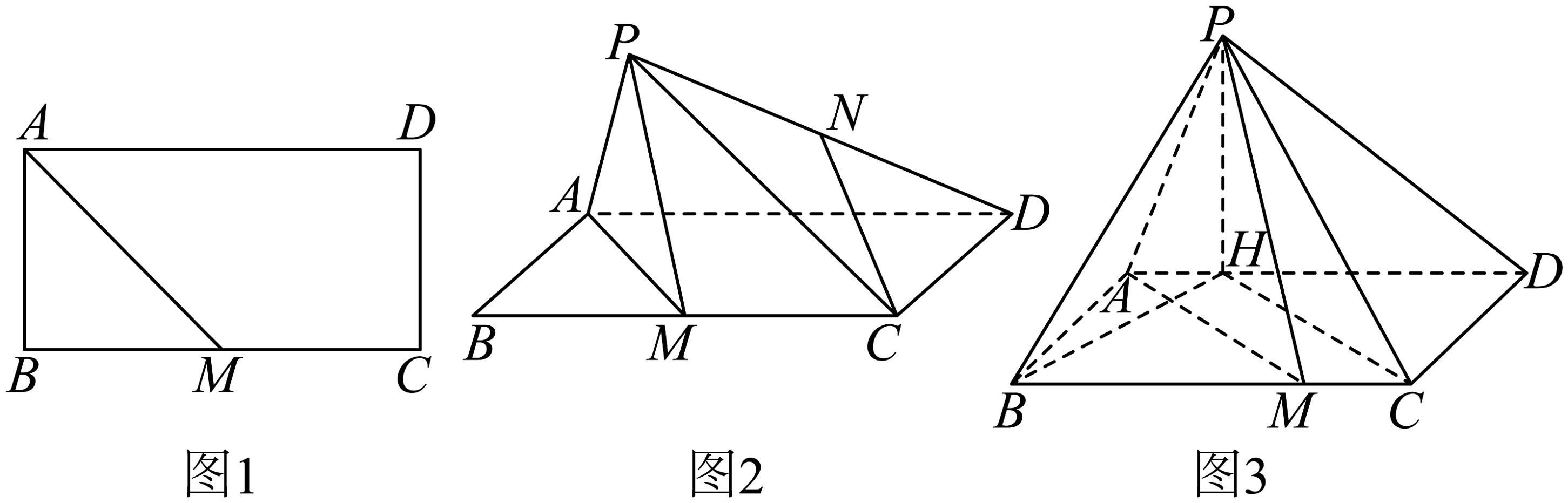 (1)、如图2,若M是BC的中点,点N是线段PD的中点,求证:平面PAM;(2)、如图3,若点P在平面AMCD内的射影H落在线段AD上.
(1)、如图2,若M是BC的中点,点N是线段PD的中点,求证:平面PAM;(2)、如图3,若点P在平面AMCD内的射影H落在线段AD上.①求证:平面PAD;
②求点M的位置,使三棱锥的外接球的体积最大,并求出最大值.
-
16、已知的内角 , , 的对边分别为 , , .且满足.(1)、求角;(2)、已知的外接圆的圆心为 , 半径.
(i)作角的平分线交于 , , 求的面积;
(ii)若 , 求的取值范围.
-
17、某校数学建模社团招聘社长职位分笔试与面试两个环节,在笔试中有两轮答题:第一轮从类的5个问题中任选两题作答,若两题都答对,则得40分,否则得0分;第二轮从类的5个问题中任选两题作答,每答对1题得30分,答错得0分.若两轮总分不低于60分则进入面试环节.小红和小明参加此次招聘活动,已知小红对类每个问题的答对的概率均为0.5.在类的5个问题中,小明只能答对4个问题,在类的5个问题中,小明每个问题答对的概率都为0.4.他们回答任一问题正确与否互不影响.(1)、求小明在第一轮得40分的概率;(2)、求小红两轮总分得60分的概率;(3)、试判断小红和小明谁更有机会进入面试环节?
-
18、如图,四棱锥的各个顶点均在球的表面上,且平面.
 (1)、证明:平面平面;(2)、求四棱锥体积的最大值;
(1)、证明:平面平面;(2)、求四棱锥体积的最大值; -
19、在中,.(1)、求的值;(2)、若 , 再从下列三个条件中选择一个作为已知,使存在,求的面积.
条件①:;条件②:;条件③:.
注:如果选择的条件不符合要求,第(Ⅱ)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.
-
20、在平面四边形中, , 分别为 , 的中点,若 , , 且 , 则 .