相关试卷
-
1、已知圆:和圆: , 则两圆公共弦所在直线的方程为.
-
2、如图,在中, , , , 过中点的直线与线段交于点 . 将沿直线翻折至 , 且点在平面内的射影在线段上,连接交于点 , 是直线上异于的任意一点,则( )
 A、 B、 C、点的轨迹的长度为 D、直线与平面所成角的余弦值的最小值为
A、 B、 C、点的轨迹的长度为 D、直线与平面所成角的余弦值的最小值为 -
3、数列2,0,2,0,…的通项公式可以是( )A、 B、 C、 D、
-
4、已知双曲线C:( , )的左、右焦点分别为 , , 过的直线分别交双曲线左、右两支于A、B两点,点C在x轴上, , 平分 , 则双曲线C的离心率为( )A、 B、 C、 D、
-
5、一个半径为1的小球在一个内壁棱长为的正四面体封闭容器内可向各个方向自由运动,则该小球表面永远不可能接触到的容器内壁的面积是( )A、 B、 C、 D、
-
6、展开式中的常数项为( )A、15 B、60 C、 D、240
-
7、 , , , 若 , , 共面,则实数k为( )A、1 B、2 C、3 D、4
-
8、已知是关于复数z的方程(m,)的一根,则( )A、5 B、6 C、7 D、8
-
9、抛物线的焦点坐标为( )A、 B、 C、 D、
-
10、已知为复数,则下列说法正确的是( )A、 B、 C、若 , 则 D、若 , 则或
-
11、已知集合 , , 则( )A、 B、 C、 D、
-
12、如图,八面体的每一个面都是边长为4的正三角形,且顶点在同一个平面内.若点在四边形内(包含边界)运动,为的中点,则( )
 A、当为的中点时,异面直线与所成角为 B、当平面时,点的轨迹长度为 C、当时,点到的距离可能为 D、存在一个体积为的圆柱体可整体放入内
A、当为的中点时,异面直线与所成角为 B、当平面时,点的轨迹长度为 C、当时,点到的距离可能为 D、存在一个体积为的圆柱体可整体放入内 -
13、如图,在中, , D在边AB上, , , 则( )
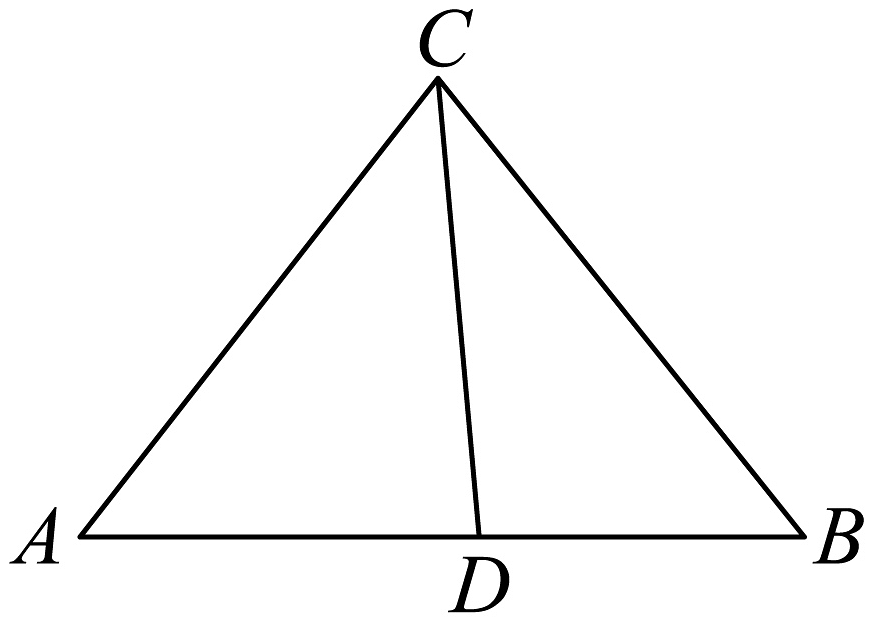 A、 B、 C、 D、
A、 B、 C、 D、 -
14、已知函数.(1)、若 , 求的值;(2)、判断在上的单调性并利用定义法证明;(3)、求在上的最大值.
-
15、已知二次函数 .(1)、当取何值时,不等式对一切实数都成立?(2)、若在区间内恰有一个零点,求实数的取值范围.
-
16、已知集合 , .(1)、若 , 求;(2)、若“”是“”的必要不充分条件,求的取值范围.
-
17、已知角的终边经过点.(1)、求 , 的值;(2)、求的值.
-
18、已知函数 , 若关于的方程有四个不相等的实数根,则的取值范围是.
-
19、已知 , , 则.(用表示)
-
20、若函数在区间上的值域为 , 则称为函数的“保值区间”,下列说法正确的是( )A、函数存在保值区间 B、函数存在保值区间 C、若一次函数存在保值区间,则或 D、若函数存在保值区间,则实数的取值范围为