-
1、 比较-3.14与-π的大小.
-
2、下列各数中,哪些是有理数,哪些是无理数?
0.4583, 3. , - π,- , 18.
-
3、下列各数中,哪些是有理数,哪些是无理数?
3.14,- , 0. , 0.1010001000001…(相邻两个1之间0的个数逐次加2).
-
4、如图,等边三角形ABC的边长为2,高为h,h可能是有理数吗?

-
5、归纳是数学发现的重要方法,但仅仅由几种特殊情况归纳出来的结论并不可靠.请你查阅资料,了解数学史上有关这方面的一些事例,并在班级内分享.
-
6、 如图,AB∥DE,BC∥EF, 你能判断∠ABC与的大小关系吗?小颖据此得出结论:如果两个角的两边分别平行,那么这两个角相等.你认为她的判断正确吗?

-
7、观察下列各式:
.
你能否得到结论“所有奇数都可以表示为两个自然数的平方差”?所有偶数呢?请说明理由.
-
8、八(1)班有39名同学,他们每人将自己的学号作为n的取值( 3,…,39)代入式子 结果发现式子 的值都是质数,于是他们猜想:对于所有的自然数,式子 的值都是质数.
你认为这个猜想正确吗?
-
9、 当n为正整数时, 的值一定是质数吗?
-
10、
 (1)、图(1)中有三条线段a,b,c,哪一条和线段d在同一条直线上?请你先观察,再用直尺验证一下.(2)、图(2)中两条线段a与b的长度相等吗?
(1)、图(1)中有三条线段a,b,c,哪一条和线段d在同一条直线上?请你先观察,再用直尺验证一下.(2)、图(2)中两条线段a与b的长度相等吗? -
11、 已知长方形纸片 , 点E , F在上,点G , H在上,将纸片分别沿 , 折叠,A、B、C , D的对应点分别为 , , , , 记 , .
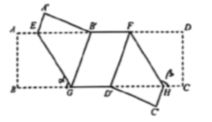 (1)、如图,已知点在上,点在上.
(1)、如图,已知点在上,点在上.①若 , 求的度数.
②若 , 求与β满足的关系式.
(2)、若所在直线与所在直线互相垂直,请直接写出与β满足的关系式. -
12、 某景区计划用160万元资金采购若干机器狗和无人机运送货物.已知购进2只机器狗和3台无人机需54万元,购进4只机器狗和1台无人机需58万元.(1)、求机器狗和无人机的采购单价.(2)、满载情况下,每只机器狗比每台无人机单次多载 , 运送货物所需的机器狗数量恰好与运送货物所需的无人机数量相同,求机器狗和无人机的单次最高载货量.(3)、若两种设备均要采购且资金恰好全部用完,请根据上述信息列出所有的采购方案.并通过计算说明哪种方案的单次载货总量最高.
-
13、 一列整式依次为: , , , , …;
另一列整式依次为: , , , .
(1)、求和 . (用含m的代数式表示)(2)、求和 , 并归纳出的规律.(用含m , n的代数式表示)(3)、若 , 求m的值. -
14、(1)、若展开后不含x的一次项,求k的值.(2)、先化简,再求值: , 其中 .
-
15、 解下列方程(组):(1)、 .(2)、 .
-
16、 某校为加强学生的安全意识,提高自我防护能力,组织全体学生开展“安全知识”竞赛活动,从中随机拍取部分学生的成绩(满分100分)进行统计,按照成绩(记为x)分为 , , , , 五个等级.下图给出两幅不完整的成绩统计图.
部分学生“安全知识”竞赛得分频数直方图

部分学生“安全知识”竞赛得分扇形统计图
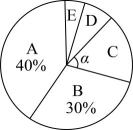
请根据以上信息,解答下列问题:
(1)、求本次调查的样本容量和扇形统计图中圆心角α的度数,并补全频数直方图.(2)、学校将对竞赛成绩低于70分的学生举办安全教育讲座,请估计该校1000名学生中需参加讲座的人数. -
17、 因式分解:(1)、 .(2)、 .
-
18、 计算:(1)、 .(2)、 .
-
19、 将边长分别为m , 的两个正方形按如图所示方式摆放,其中点B , C , E在同一条直线上,点G在上,记阴影部分面积为S . 若 , , 则的值为 .

-
20、 若二元一次方程组的解满足或 , 则称该方程组为“二倍解方程组”.已知关于x , y的方程组是“二倍解方程组”,则m的值为 .