-
1、如图,在矩形中,边绕点B顺时针旋转到的位置,点A的对应点E落在边的中点,若 , 则点A旋转到点E的路径长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
2、如图,是红、黄两队某局冰壶比赛结束后的冰壶分布图.以大本营内的中心点O为原点,建立如图所示的平面直角坐标系.按比赛规则,更靠近原点的冰壶为本局胜方,则决定胜负的那个冰壶所在位置位于( )
 A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、第一象限 B、第二象限 C、第三象限 D、第四象限 -
3、如图,在一间黑屋子里,用一盏白炽灯照射直角三角板形成影子 , 三角板始终保持与地面平行,它向白炽灯靠近的过程中(不与光源接触),下列说法正确的是( )
 A、越来越大 B、影子不是直角三角形 C、影子越来越小 D、影子越来越大
A、越来越大 B、影子不是直角三角形 C、影子越来越小 D、影子越来越大 -
4、下列计算正确的是( )A、 B、 C、 D、
-
5、深圳远足径“三径三线”全线贯通,总长420000米,这标志着“山海连城”计划迎来了一个新的里程碑.数据420000用科学记数法可表示为( )A、 B、 C、 D、
-
6、下列中国传统装饰纹样中,为中心对称图形的是( )A、四合云纹
 B、葫芦纹
B、葫芦纹 C、如意纹
C、如意纹 D、莲花纹
D、莲花纹
-
7、如图,数轴上的下列四点中,最可能表示的点是( )
 A、点A B、点B C、点C D、点D
A、点A B、点B C、点C D、点D -
8、为满足市场需求,某超市购进一种品牌水果,每箱进价是50元.超市规定每箱售价不得少于56元.根据以往销售经验发现:当售价定为每箱56元时,每天可以卖出300箱,每箱售价每提高1元,每天要少卖出10箱.(1)、试求出每天的销售量(箱)与每箱售价(元)之间的函数关系式;(2)、当每箱售价定为多少元时,每天销售的利润(元)最大?最大利润是多少?(3)、为稳定物价,有关管理部门限定:这种水果的每箱售价不得高于65元.如果超市想要每天获得不低于2030元的利润,那么超市每天至少销售这种水果多少箱?
-
9、如图,已知是的直径,弦与弦交于点 , 且 , 垂足为点 , 若 .
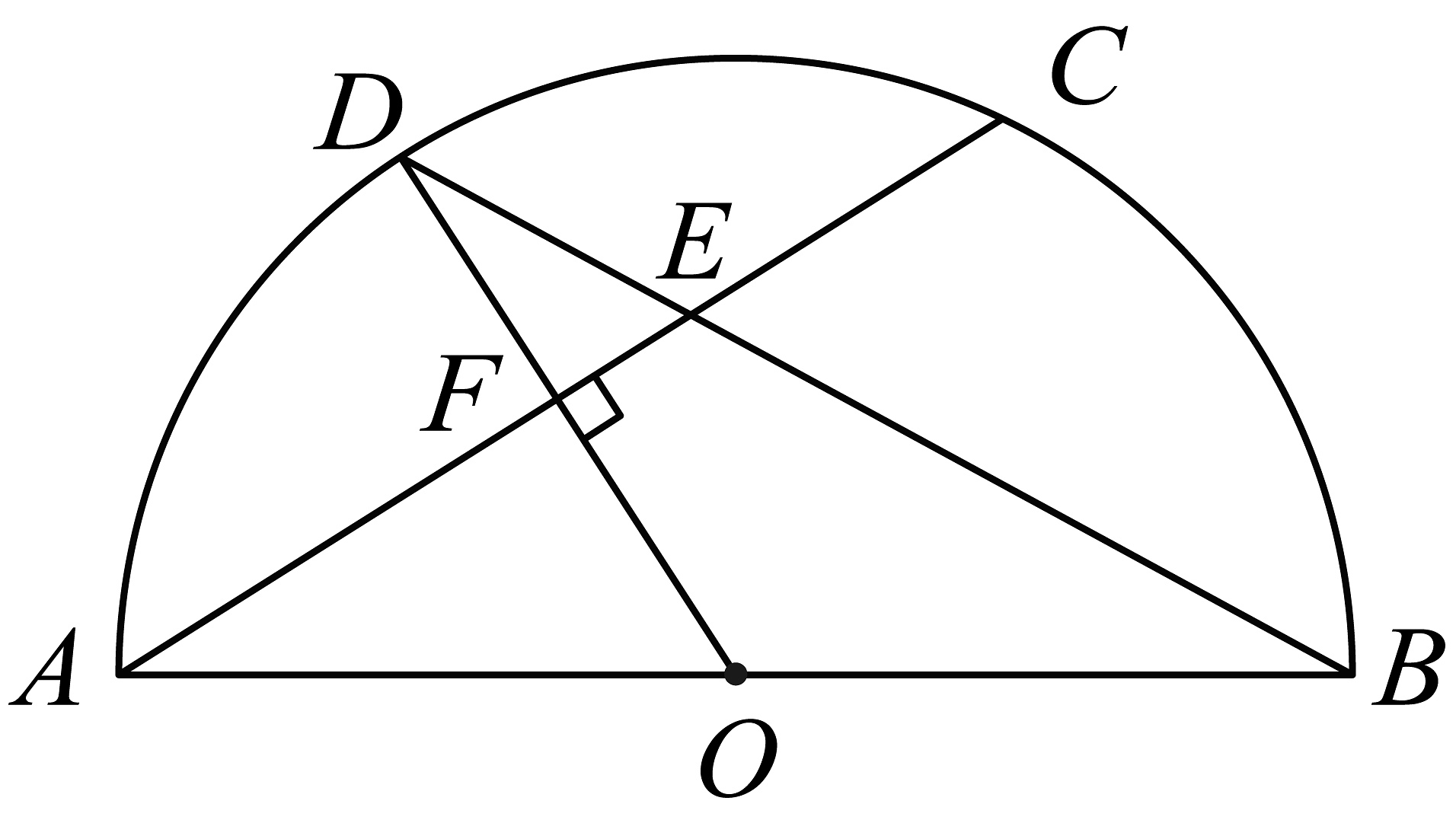 (1)、求的度数;(2)、若 , 求的值;(3)、在(2)的基础上求的值.
(1)、求的度数;(2)、若 , 求的值;(3)、在(2)的基础上求的值. -
10、在平面直角坐标系中,已知四边形为矩形,其中点 , .
 (1)、当反比例函数()的图象和矩形有交点时,求k的最大值;(2)、如图,反比例函数()的图象与 , 分别交于点D,E,连接 , , . 当时,求的面积.
(1)、当反比例函数()的图象和矩形有交点时,求k的最大值;(2)、如图,反比例函数()的图象与 , 分别交于点D,E,连接 , , . 当时,求的面积. -
11、某班的同学想测量教学楼的高度,大楼前有一段斜坡 , 已知的长为8米,它的坡比 , 从C点向前进30米后,又在D处测得教学楼顶端A的仰角为 .
 (1)、_________;(2)、求点C到的距离;(3)、教学楼的高度约为多少米.(结果精确到米)(参考数据: , , , )
(1)、_________;(2)、求点C到的距离;(3)、教学楼的高度约为多少米.(结果精确到米)(参考数据: , , , ) -
12、某工厂计划购买A,B两种工艺品共400件奖励优秀员工.已知A种工艺品的单价比B种工艺品的单价高50元,用600元单独购买A种工艺品与用450元单独购买B种工艺品的数量相同.(1)、A,B两种工艺品的单价各为多少元?(2)、若该工厂计划购买A,B两种工艺品总费用不超过30500元,且购买A种工艺品不少于5件,则该工厂共有几种购买方案?
-
13、某校在学生中对预防诺如病毒相关知识知晓情况进行专项调查,采取随机抽样的方式抽取50人进行问卷调查,问卷调查分为A、B、C、D四个选项.每人必选且只选其中一项,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”.调查后的数据整理成不完整的统计表和四个选项所占比的扇形统计图如下:
A
B
C
D
频数
14
21
x
y
 (1)、表中的 , ;(2)、若该校有1000名学生,根据调查结果估计该校学生中对预防诺如病毒相关知识“比较了解”的人数;(3)、若王老师和李老师要到选择某一选项的学生中进一步了解情况,试用列表或画树状图的方法求两人选择同一选项的学生了解情况的概率.
(1)、表中的 , ;(2)、若该校有1000名学生,根据调查结果估计该校学生中对预防诺如病毒相关知识“比较了解”的人数;(3)、若王老师和李老师要到选择某一选项的学生中进一步了解情况,试用列表或画树状图的方法求两人选择同一选项的学生了解情况的概率. -
14、(1)计算:
(2)解不等式组: , 并把解集在数轴上表示出来
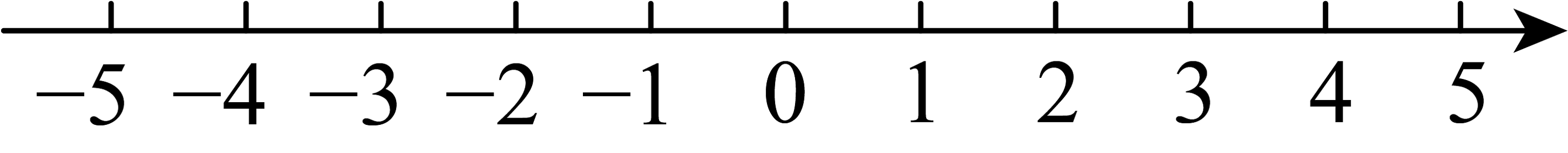
-
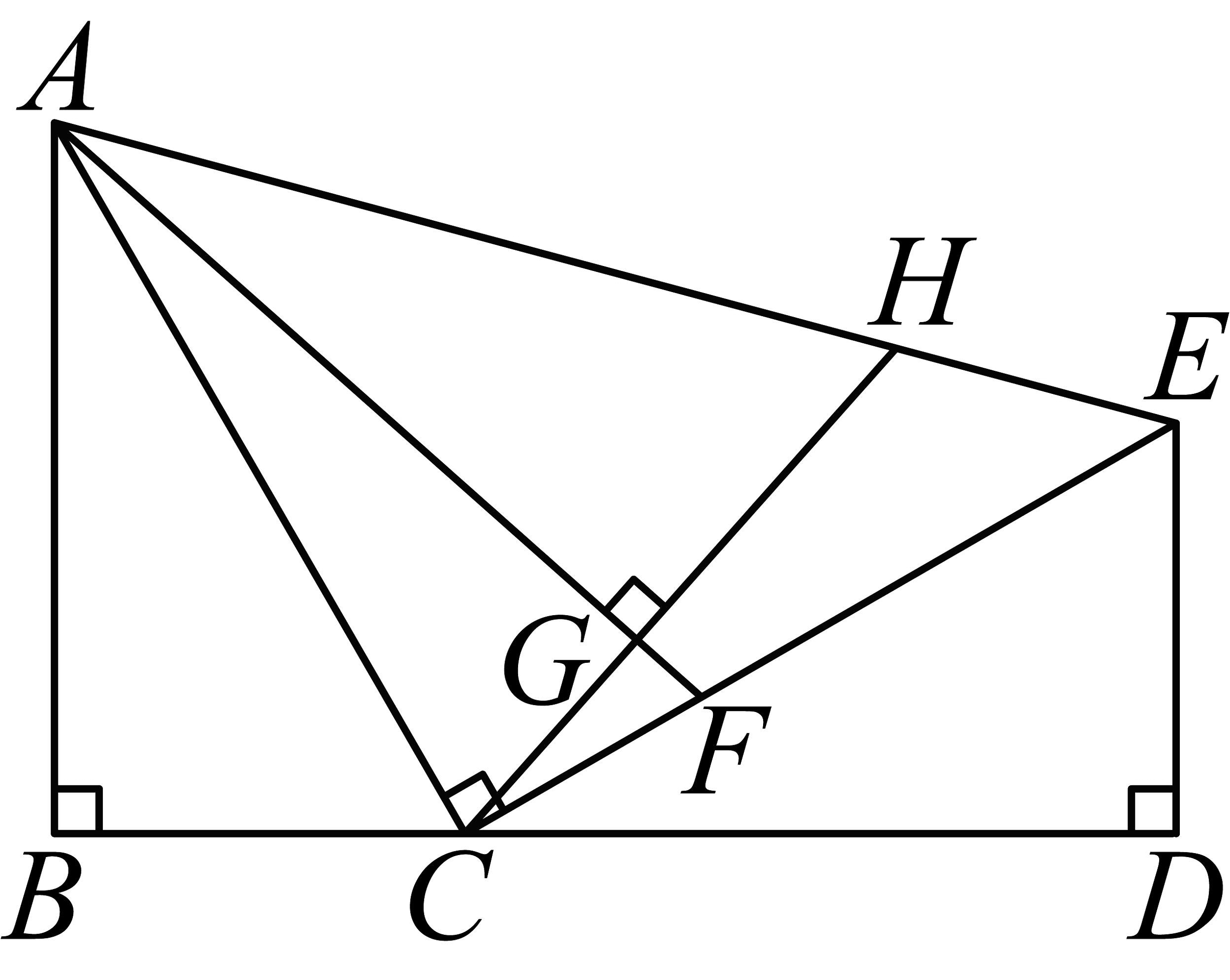
15、如图,在四边形中, , 点C是边上一点,且 , 取的三等分点F , 连接 , 过点C作交于点G,延长交于点H,若 , 则的长为 .
-
16、用反证法证明命题“如果 , 那么”的第一步应假设 .
-
17、已知一组数据4,8,x,6的众数为6,则该组数据的平均数为 .
-
18、若函数是关于x的正比例函数,则k满足的条件为 .
-
19、如图,与相交于点O,且 . 若 , 则的值为( )
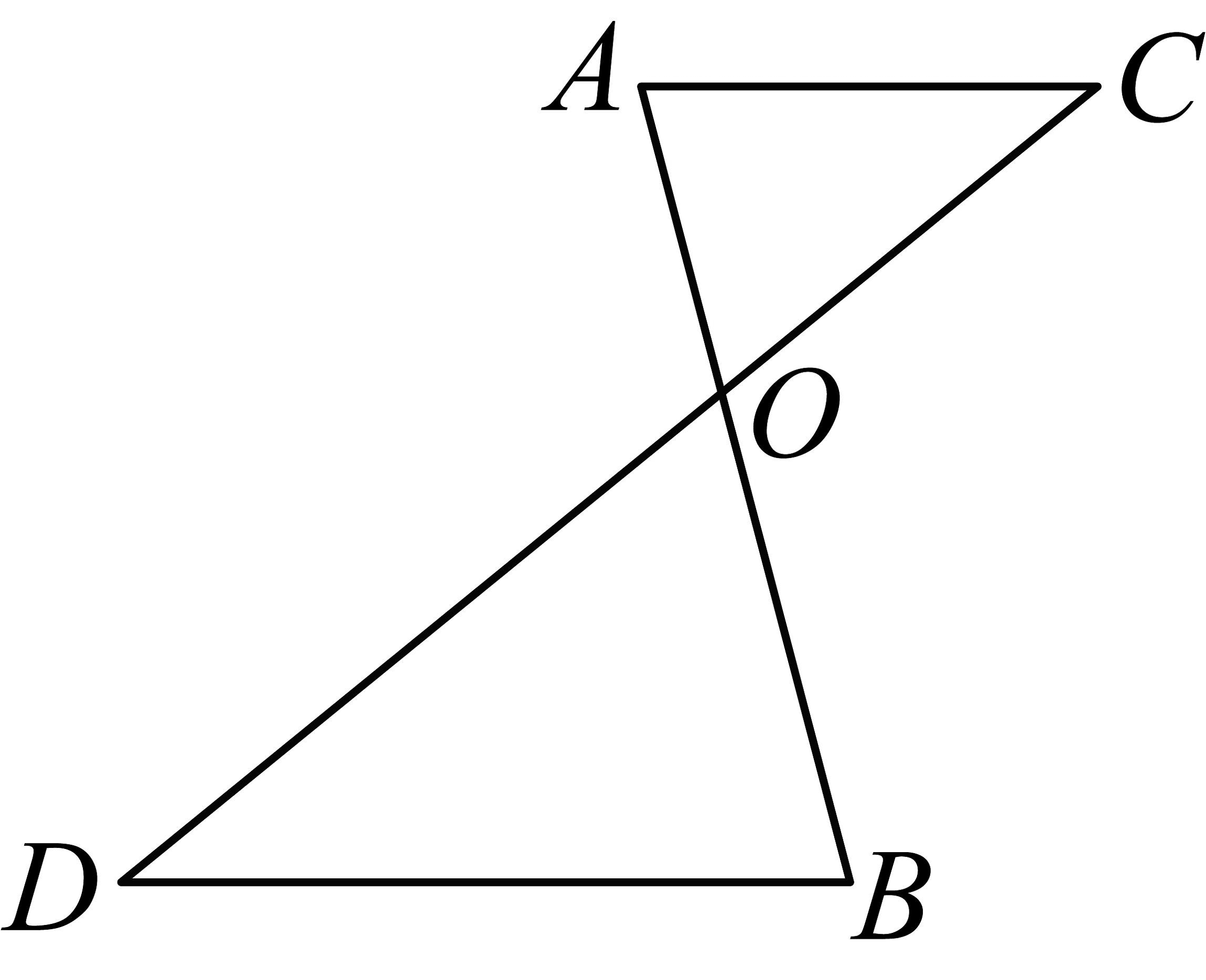 A、1 B、 C、 D、
A、1 B、 C、 D、 -
20、若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、