相关试卷

1、小敏和小慧去西湖风景区游玩，约好在少年宫广场见面。如图1，A地、B地、少年宫广场在一条直线上.小敏从A地出发，先匀速步行至车站，再坐公交车前往少年宫广场.同时，小慧从B地出发，骑车去少年宫广场，平均速度为200米/分钟.两人距离A地的路程s（米）和所经过的时间t（分）之间的函数关系如图2所示。（公交车的停车时间忽略不计）

(1)、求公交车的平均速度。

(2)、求同时出发后，经过多少时间小敏追上小慧.

(3)、在小敏坐公交车的过程中，当她与小慧相距400米时，求t的值.

查看解析
2、老师布置了一道思考题：“尺规作图：过直线AB外一点P作这条直线的平行线，”小亮的作法如下：如图，在直线AB上任取一点C，以点C为圆心，CP的长为半径画弧交AB于点D，再分别以点P，D为圆心，CP的长为半径画弧，两弧交于点E，作直线PE，则PEIIAB.

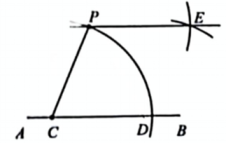(1)、请判断小亮的作法是否正确，并说明理由。

(2)、连接PD，CE，交点为O，若PC=5，PD=6，求点P到直线AB的距离.

查看解析
3、在直角坐标系中，函数y= $\frac{k}{x}$ （k>0）与函数y=2x的图象交于两个不同的点A，B.点A的横坐标为2.

(1)、求k的值和点B的坐标.

(2)、若函数y=2x的图象向下平移m（m>0）个单位后经过点C（3，1），与y轴交于点D.
①求m的值.
②求△ABD的面积.

查看解析
4、如图，在△ABC中，AD=3 $\sqrt{2}$ ， BD=DC=4，∠ADC=45°·

(1)、求线段AC的长.

(2)、求tan∠ABC的值.

查看解析
5、某中学举行“垃圾分类投放和分类处理”知识竞赛，随机抽取部分学生的成绩进行统计，并绘制成如图所示的未完成的频数表与频数分布直方图，（每一组不含前一个边界值，含后一个边界值）
抽取的学生的成绩频数表
组别/分
频数
频率
60～70
5
a
70～80
10
0.2
80～90
b
c
90~100
18
0.36
请根据所给信息，解答下列问题：

(1)、填空：a= ， b= ， c=.

(2)、补全频数分布直方图。

(3)、若成绩在80分以上为优秀，请你根据抽取的样本数据，估计参加这次比赛的800名学生中成绩优秀的学生约有多少名？

查看解析
6、计算：

(1)、 $| - 4 | - (- 3)^{2} \times 2$ .

(2)、 $\frac{1}{x - 1} - \frac{x}{x - 1}$ .

查看解析
7、如图，在 $△ A B C$ 中， $∠ B A C = 9 0^{°}$ ， $A B = A C$ ，点O为BC中点，连接AO，正方形ODEF在 $△ A B C$ 内部，边EF交AO于点G，连接AF，CE.若点G为EF中点， $A F = \sqrt{17}$ ， $E F = \sqrt{5}$ ，则线段CE的长为

查看解析
8、如图，款式相同的4个碗叠放在一起总高度为11.5cm，若同款的7个碗叠放在一起总高度为16cm，则一个碗的高度为cm.

查看解析
9、如图，PA，PB为OO的两条切线，点A，B为切点，点C在劣弧AB上.若∠ACB=115°，则∠P的度数为.

查看解析
10、一个不透明的袋子中有4个白球，2个红球和a个黑球，它们除颜色外其余都相同，从中随机摸一个球，摸到黑球的概率为 $\frac{2}{5}$ ，则a的值为.

查看解析
11、若二次根式 $\sqrt{2 - a}$ 有意义，则a的取值范围为.

查看解析
12、已知△ABC中，AB²=AC（AC+BC），则（）

A、∠ABC=2∠ACB B、∠ACB=2∠ABC C、∠ACB=2∠BAC D、∠BAC=2∠ABC

查看解析
13、若 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - m x + 15 = 0$ 的两个实数根， $x_{1} - x_{2} = 2$ ，则m的值为（）

A、 $\pm 8$ B、8 C、-8 D、 $\pm 4$

查看解析
14、反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像在第二、四象限，则二次函数 $y = k x^{2} + 4 x$ 的大致图像的是（）

A、 B、 C、 D、

查看解析
15、如图，AB为 $⊙ O$ 的直径，点 $C$ 在 $⊙ O$ 上，若 $A B = 2 A C = 6$ ，则 $\overset{⌢}{B C}$ 长为（）

A、 $\frac{π}{2}$ B、 $π$ C、 $2 π$ D、 $4 π$

查看解析
16、如图，在 $△ A B C$ 中，点D在BC边上， $E G ∥ B C$ ，分别交AB，AD，AC于点E，F，G，则（）

A、 $\frac{A E}{E B} = \frac{E F}{B D}$ B、 $\frac{E F}{B D} = \frac{F G}{D C}$ C、 $\frac{A E}{A B} = \frac{E F}{E G}$ D、 $\frac{A F}{F D} = \frac{A G}{A C}$

查看解析
17、据调查，某班30名学生所穿鞋子鞋号统计如下：
鞋号
20
21
22
23
24
频数
1
8
6
14
1
则该班学生所穿鞋子鞋号的中位数和众数分别是（）

A、6，14 B、22.5，14 C、22.5，23 D、22，23

查看解析
18、下列各式中，运算结果为6m⁵的是（）

A、2m³+4m² B、（-3m³）² C、12m⁵÷（2m） D、2m²·3m³

查看解析
19、2025年4月30日，神舟十九号载人飞船返回舱在东风着陆场成功着陆，标志着神舟十九号载人飞行任务取得圆满成功，据悉，神舟十九号载人飞船在绕地球轨道飞行时的动能大约为228000000000焦耳.数据228000000000用科学记数法表示为（）

A、0.228×10¹² B、2.28×10¹¹ C、22.8×10¹¹ D、228×10⁹

查看解析
20、以下图标，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析

上一页 312 313 314 315 316 下一页跳转

组别/分	频数	频率
60～70	5	a
70～80	10	0.2
80～90	b	c
90~100	18	0.36

鞋号	20	21	22	23	24
频数	1	8	6	14	1