高中物理人教版必修2第六章第4节万有引力理论的成就同步练习
试卷更新日期：2018-01-29 类型：同步测试
一、选择题
-
1. 科学家们推测，太阳系除八大行星之外的另一颗行星就在地球的轨道上，从地球上看，它永远在太阳的背面，人类一直未能发现它，可以说是“隐居”着的地球的“孪生兄弟”．由以上信息可以确定（ ）A、这颗行星的公转周期与地球相等 B、这颗行星的半径等于地球的半径 C、这颗行星的密度等于地球的密度 D、这颗行星的质量2. 有一星球的密度与地球的密度相同，但它表面处的重力加速度是地面上重力加速度的4倍，则该星球的质量将是地球质量的（ ）A、 B、4倍 C、16倍 D、64倍3. 质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动．已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的（ ）A、线速度v＝ B、角速度ω＝ C、运行周期T＝π D、向心加速度a＝4. 宇宙中两颗相距很近的恒星常常组成一个双星系统．它们以相互间的万有引力彼此提供向心力，从而使它们绕着某一共同的圆心做匀速圆周运动，若已知它们的运转周期为T，两星到某一共同圆心的距离分别为R1和R2 ， 那么，这双星系统中两颗恒星的质量关系描述不正确的是（ ）A、这两颗恒星的质量必定相等 B、这两颗恒星的质量之和为 C、这两颗恒星的质量之比为m1∶m2＝R2∶R1 D、必有一颗恒星的质量为
二、多项选择题
-
5. 下列说法正确的是（ ）A、海王星和冥王星是人们依据万有引力定律计算出轨道而发现的 B、天王星是人们依据万有引力定律计算出轨道发现的 C、天王星的运行轨道偏离根据万有引力定律计算出来的轨道，其原因是天王星受到轨道外面其他行星的引力作用 D、以上说法都不对6. 一卫星绕地球做匀速圆周运动，其轨道半径为r，卫星绕地球做匀速圆周运动的周期为T，已知地球的半径为R，地球表面的重力加速度为g，引力常量为G，则地球的质量可表示为（ ）A、 B、 C、 D、7. 土星外层有一个环，为了判断它是土星的一部分还是土星的卫星群，可以测量环中各层的线速度v与该层到土星中心的距离R之间的关系，则下列判断正确的是（ ）A、若v2∝R则该层是土星的卫星群 B、若v∝R则该层是土星的一部分 C、若v∝ 则该层是土星的一部分 D、若v2∝ 则该层是土星的卫星群
三、双选题
-
8. 如图所示，飞行器P绕某星球做匀速圆周运动，星球相对飞行器的张角为θ ， 万有引力常量为G ， 下列说法正确的是( ）
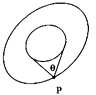A、轨道半径越大，周期越长 B、轨道半径越大，速度越大 C、若测得周期和张角，可得到星球的平均密度 D、若测得周期和轨道半径，可得到星球的平均密度四、填空题
-
9. 假设在半径为R的某天体上发射一颗该天体的卫星，若它贴近该天体的表面做匀速圆周运动的运行周期为T1 ， 已知引力常量为G，则该天体的密度为 ． 若这颗卫星距该天体表面的高度为h，测得在该处做圆周运动的周期为T2 ， 则该天体的密度又可表示为 ．10. 两个行星质量分别为m1和m2 ， 绕太阳运行的轨道半径分别是r1和r2 ， 则它们与太阳间的万有引力之比为 ． 它们的公转周期之比 ．
五、计算题
-
11. 土星周围有许多大小不等的岩石颗粒，其绕土星的运动可视为圆周运动．其中有两个岩石颗粒A和B与土星中心的距离分别为rA＝8.0×104km和rB＝1.2×105km，忽略所有岩石颗粒间的相互作用．（结果可用根式表示）(1)、求岩石颗粒A和B的线速度之比．(2)、土星探测器上有一物体，在地球上重为10N，推算出它在距土星中心3.2×105km处受到土星的引力为0.38N．已知地球半径为6.4×103km，请估算土星质量是地球质量的多少倍？
12. 已知地球半径R＝6.4×106m，地面附近重力加速度g＝9.8m/s2 ． 计算在距离地面高为h＝2×106m的圆形轨道上的卫星做匀速圆周运动的线速度v和周期T．
-