湖南省张家界市永定区2016-2017学年八年级上册数学期末考试试卷
试卷更新日期:2018-01-17 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组数为边长能构成直角三角形的是( )A、1,1, B、2,3,4 C、4,5,6 D、6,8,113. 在下列所给出坐标的点中,在第三象限的是( )A、(2,3) B、(-2,-3) C、(-2,3) D、(2,-3)4. 如图,在△ 中, , ,BC=4cm,点D为AB的中点,则 ( )
2. 以下列各组数为边长能构成直角三角形的是( )A、1,1, B、2,3,4 C、4,5,6 D、6,8,113. 在下列所给出坐标的点中,在第三象限的是( )A、(2,3) B、(-2,-3) C、(-2,3) D、(2,-3)4. 如图,在△ 中, , ,BC=4cm,点D为AB的中点,则 ( )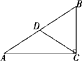 A、3cm B、4cm C、5cm D、6cm5. 已知▱ABCD的周长是26cm,其中△ABC的周长是18cm,则AC的长为( )A、12cm B、10cm C、8cm D、5cm6. 菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为( )A、40 cm B、20 cm C、10 cm D、5 cm7. 正方形具有而菱形不一定具有的性质是( )A、对角线平分一组对角 B、对角线互相垂直平分 C、对角线相等 D、四条边相等8. 汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为( )A、
A、3cm B、4cm C、5cm D、6cm5. 已知▱ABCD的周长是26cm,其中△ABC的周长是18cm,则AC的长为( )A、12cm B、10cm C、8cm D、5cm6. 菱形的两条对角线长为6 cm 和8 cm,那么这个菱形的周长为( )A、40 cm B、20 cm C、10 cm D、5 cm7. 正方形具有而菱形不一定具有的性质是( )A、对角线平分一组对角 B、对角线互相垂直平分 C、对角线相等 D、四条边相等8. 汽车由重庆驶往相距400千米的成都,如果汽车的平均速度是100千米/时,那么汽车距成都的路程s(千米)与行驶时间t(小时)的函数关系用图象表示为( )A、 B、
B、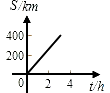 C、
C、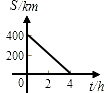 D、
D、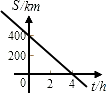
二、填空题
-
9. 已知点P(3,2)在一次函数 的图象上,则b=.
10. 一个多边形的内角和是它的外角的和的2倍,这个多边形的边数是
11. 已知y与x成正比例,且当x=1时,y=2,则当x=4时,y=.
12. 如图,AC⊥BC,AD⊥BD,垂足分别是C、D,若要用“HL”得到Rt△ABC≌Rt△BAD,则你添加的条件是.(写一种即可)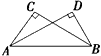 13. 将点P (-3,4)先向下平移3个单位,再向左平移2个单位后得到点Q,则点Q的坐标是。
13. 将点P (-3,4)先向下平移3个单位,再向左平移2个单位后得到点Q,则点Q的坐标是。
14. 如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形的周长为 .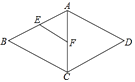 15. 如图,矩形ABCD中,对角线AC和BD交于点O,过O的直线分别交AD和BC于点E、F,已知AD=4 cm,图中阴影部分的面积总和为6 cm 2 , 则矩形的对角线AC长为cm.
15. 如图,矩形ABCD中,对角线AC和BD交于点O,过O的直线分别交AD和BC于点E、F,已知AD=4 cm,图中阴影部分的面积总和为6 cm 2 , 则矩形的对角线AC长为cm.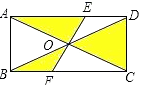 16. 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).
16. 如图所示,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n为自然数)的坐标为(用n表示).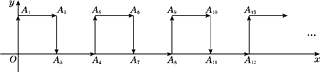
三、解答题
-
17. 在边长为1的小正方形网格中,△AOB的顶点均在格点上.
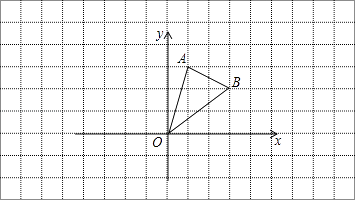 (1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;
(1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;
(3)、在(2)的条件下,A1的坐标为 .
18. 已知:如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.求证:BE=DF.
 19. 已知一次函数 .(1)、若这个函数的图象经过原点,求m的值;
19. 已知一次函数 .(1)、若这个函数的图象经过原点,求m的值;
(2)、若这个函数的图象经过一、三、四象限,求m的取值范围.
20. 如图,已知四边形 中, , , , , ,求四边形 的面积.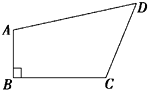 21. 为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:
21. 为了进一步了解某校八年级学生的身体素质情况,体育老师对该校八年级(1)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:组别
次数x
频数(人数)
第1组
80≤x<100
6
第2组
100≤x<120
8
第3组
120≤x<140
a
第4组
140≤x<160
18
第5组
160≤x<180
6
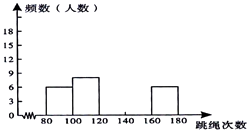
请结合图表完成下列问题:
(1)、求表中a的值;(2)、请把频数分布直方图补充完整;
(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?
22. 如图 , 在菱形ABCD中,∠ABC与∠BAD的度数比为1∶2,周长是32cm . 求: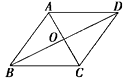 (1)、两条对角线的长度;(2)、菱形的面积.23. 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)、两条对角线的长度;(2)、菱形的面积.23. 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地. 如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题: (1)、线段CD表示轿车在途中停留了h;
(1)、线段CD表示轿车在途中停留了h;
(2)、货车的平均速度是km/h;
(3)、求线段DE对应的函数解析式.
24. 如图,在矩形ABCD中,AB=1cm,AD=3cm,点Q从A点出发,以1cm/s的速度沿AD向终点D运动,点P从点C出发,以1cm/s的速度沿CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动,两点同时出发,运动了t秒.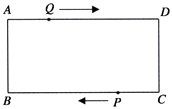 (1)、当0<t<3,判断四边形BQDP的形状,并说明理由;
(1)、当0<t<3,判断四边形BQDP的形状,并说明理由;
(2)、求四边形BQDP的面积S与运动时间t的函数关系式;
(3)、求当t为何值时,四边形BQDP为菱形.