湖北省十堰市2016-2017学年八年级上册数学期末考试试卷
试卷更新日期:2018-01-17 类型:期末考试
一、单选题
-
1. 下列长度的三条线段能构成三角形的是( )A、3,4,8 B、3,4,7 C、5,6,10 D、5,6,11
-
2. 下列几何图形不一定是轴对称图形的是( )A、角 B、等边三角形 C、等腰三角形 D、直角三角形
-
3. 下列语句正确的是( )A、三角形的三条高都在三角形内部 B、三角形的三条中线交于一点 C、三角形不一定具有稳定性 D、三角形的角平分线可能在三角形的内部或外部
-
4. 如图,AD和BC相交于O点,OA=OC , 用“SAS”证明△AOB≌△COD还需( )
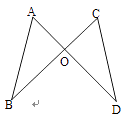 A、AB=CD B、OB=OD C、∠A=∠C D、∠AOB=∠COD
A、AB=CD B、OB=OD C、∠A=∠C D、∠AOB=∠COD -
5. 下列各式运算正确的是( )A、 B、 C、 D、
-
6. 若分式 有意义,则x满足的条件是( )A、 B、 C、 D、
-
7. 下列因式分解结果正确的是( )A、 B、 C、 D、
-
8. 如图,△ABC中,BD , CD分别平分∠ABC , ∠ACB , 过点D作EF∥BC交AB , AC于点E , F , 当∠A的位置及大小变化时,线段EF和BE+CF的大小关系为( )
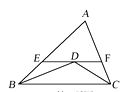 A、EF>BE+CF B、EF=BE+CF C、EF<BE+CF D、不能确定
A、EF>BE+CF B、EF=BE+CF C、EF<BE+CF D、不能确定 -
9. 若 ,则 的值为( )A、4 B、3 C、1 D、0
-
10. 如图,AD是△ABC的角平分线,DE , DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG , 其中不正确的结论的个数为( )
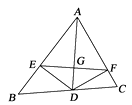 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
11. 先化简,再求值: ,其中 .
二、填空题
-
12. 中国女药学家屠呦呦获2015年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下的某种疟原虫平均长度为0.0000015米,该长度用科学记数法表示为米.
-
13. 如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线,则∠ADC= .

-
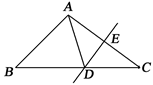
14. 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为 .
-
15. 若 ,
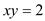 ,则代数式 的值是 .
,则代数式 的值是 . -
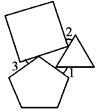
16. 将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=40°,∠2=50°,那么∠ 3的度数等于 .
-
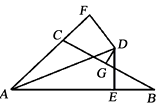
17. 如图,∠BAC的平分线与BC的垂直平分线相交于点D , DE⊥AB , DF⊥AC , 垂足分别为E , F , AB=11,AC=5,则BE= .
三、解答题
-
18. 计算:
(1)、 ;(2)、 . -
19. 因式分解:(1)、 ;(2)、
-
20. 解分式方程: +1= .
-
21. 如图,点E , F在BC上,AB=DC , ∠A=∠D , ∠B=∠C .
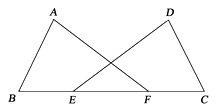
求证:BE=FC.
-
22. 如图,在平面直角坐标系中,A(2,4), B(3,1),C(-2,-1).
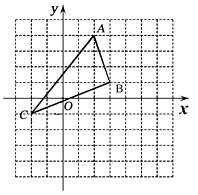 (1)、求△ABC的面积;(2)、在图中作出△ABC关于x轴的对称图形△A1B1C1 , 并写出点A1 , B1 , C1的坐标.
(1)、求△ABC的面积;(2)、在图中作出△ABC关于x轴的对称图形△A1B1C1 , 并写出点A1 , B1 , C1的坐标. -
23. 某施工队要铺设一条长为1500米的管道,为了减少施工对交通造成的影响,施工队实际的工作效率比原计划提高了20%,结果比原计划提前2天完成任务.求施工队原计划每天铺设管道多少米?
-
24. 如图1,△ABC和△ADE都是等边三角形.
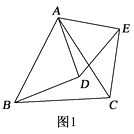 (1)、求证:BD=CE;(2)、如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.
(1)、求证:BD=CE;(2)、如图2,若BD的中点为P , CE的中点为Q , 请判断△APQ的形状,并说明理由.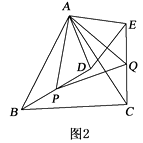
-
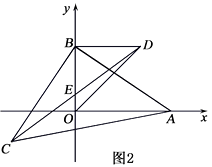
25. 已知:点A(4,0),点B是y轴正半轴上一点,如图1,以AB为直角边作等腰直角三角形ABC.
 (1)、当点B坐标为(0,1)时,求点C的坐标;(2)、如图2,以OB为直角边作等腰直角△OBD , 点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.
(1)、当点B坐标为(0,1)时,求点C的坐标;(2)、如图2,以OB为直角边作等腰直角△OBD , 点D在第一象限,连接CD交y轴于点E.在点B运动的过程中,BE的长是否发生变化?若不变,求出BE的长;若变化,请说明理由.