华东师大版数学八（下）第16章函数及其图象单元测试培优卷

试卷更新日期：2026-02-04 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10个小题，每小题3分，共30分。

1. 如图，直线l₁ 过原点，直线 l₂的表达式为 $y = - \frac{\sqrt{3}}{3} x + 2,$ 且直线 l₁和l₂ 互相垂直，交点为 P，那么直线 l₁的函数表达式为（）

A、 $y = \frac{1}{3} x$ B、 $y = \frac{\sqrt{3}}{3} x$ C、 $y = \frac{\sqrt{3}}{2} x$ D、 $y = \sqrt{3} x$

查看试题解析
2. 小明喜欢用计算机软件研究数学问题，下图是他绘制的“对勾”函数 $y = x + \frac{1}{x}$ 的图象，发现它关于原点中心对称．下面是关于函数 $y = x + 1 + \frac{1}{x - 1}$ 的描述，其中正确的是（　　）

A、函数图象的对称中心是 $(1, 1)$ B、当 $x < 1$ 时， $y$ 随 $x$ 的增大而增大 C、当 $x > 1$ 时，函数有最小值，且最小值为4 D、二次函数 $y = x^{2}$ 的图象与函数 $y = x + 1 + \frac{1}{x - 1}$ 的图象有3个不同的公共点

查看试题解析
3. 周末，小张、小李两人相约沿鲲鹏径同一路线从 $A$ 处骑行至 $B$ 处，小张、小李分别以不同的速度匀速骑行，小李比小张早出发 $5$ 分钟．小李骑行 $25$ 分钟后，小张以原速的 $\frac{8}{5}$ 继续骑行，小李骑行一段时间，小张先到达 $B$ 地，小李一直保持原速前往 $B$ 地．在此过程中，小张、小李两人相距的路程 $y$ （单位：米）与小李骑行的时间 $x$ （单位：分钟）之间的关系如图所示．有以下几个结论①小李的速度为 $300$ 米/分钟；②小张出发 $50$ 分钟追上小李；③ $A 、 B$ 两地相距 $2000$ 米；④小李比小张晚 $\frac{25}{3}$ 分钟到达 $B$ 地．其中正确的是（）

A、①② B、①④ C、①②③ D、①③④

查看试题解析
4. 如图，已知直线y= ax+2与直线y= mx+b的交点的横坐标是-2.根据图象有下列四个结论：①a>0；②b<0；③方程 ax+2= mx+b的解是 x=-2；④不等式 ax-b> mx-2的解集是x>-2.其中正确的结论个数是( )

A、1 B、2 C、3 D、4

查看试题解析
5. 已知点A(x₁ ， y₁)，B(x₂ ， y₂)在函数y=-| kx+1|+b(k，b为常数，k≠0)的图象上，下列说法正确的是( )

A、若 $y_{1} < y_{2} < b ，$ 则 $∣ x_{1} + \frac{1}{k} ∣ > ∣ x_{2} + \frac{1}{k} ∣$ B、若 $x_{1} < - \frac{1}{k} < x_{2} ，$ 则 $∣ b - y_{1} ∣ > ∣ b - y_{2} ∣ .$ C、若 $y_{1} < y_{2} < b ，$ 则 $∣ x_{1} + \frac{1}{k} ∣ < ∣ x_{2} + \frac{1}{k} ∣$ D、若 $x_{1} < - \frac{1}{k} < x_{2} ，$ 则 $∣ b - y_{1} ∣ < ∣ b - y_{2} ∣$

查看试题解析
6. 已知某手机目前电量为 $20 %$ ，经测试，在用快速充电器和普通充电器对该手机充电时，其电量 $E$ （单位：％）与充电时间 $t$ （单位：小时）的函数图象分别为图中的线段AB、AC.已知该手机正常使用时耗电量为 $10 % /$ 小时，在用快速充电器将其充满电后，正常使用 $a$ 小时，接着再用普通充电器将其充满电，其“充电——耗电——充电”的总时间是8小时，则 $a$ 的值为（）

A、 $\frac{10}{3}$ B、 $\frac{24}{7}$ C、 $\frac{27}{8}$ D、3

查看试题解析
7. 如图，过原点的直线与反比例函数y＝ $\frac{k}{x}$ （k＞0）的图象交于A、B两点，点A在第一象限，点C在x轴正半轴上，连接AC交反比例函数图象于点D，AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连接DE，若AD＝2DC，△ADE的面积为8，则k的值为（　　）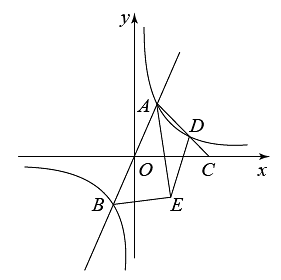

A、4 B、6 C、8 D、10

查看试题解析
8. 反比例函数 $y = \frac{1}{x}$ 的图象上有 $P (- t, y_{1})$ ， $Q (t^{2}, y_{2})$ 两点．下列正确的选项是（　　）

A、当 $t < 0$ 时， $y_{1} - y_{2} > 0$ B、当 $t > 0$ 时， $y_{1} + y_{2} > 0$ C、当 $t < - 1$ 时， $y_{1} - y_{2} > 0$ D、当 $t > 1$ 时， $y_{1} + y_{2} > 0$

查看试题解析
9. 如图，已知一次函数 $y = - \frac{3}{4} x + 3$ 的图象与x轴交于点A，与y轴交于点B，点C在线段 $A B$ 上，且 $O C = 2.4$ ，直线 $O C$ 与 $∠ O B A$ 的平分线交于D点，则点D的横坐标与它的纵坐标的和为（）

A、2.1 B、2.2 C、2.3 D、2.4

查看试题解析
10. 如图，矩形 $A O B C$ 的边 $O A = 3$ ， $O B = 4$ ，动点F在边BC上（不与B、C重合），过点F的反比例函数 $y = \frac{k}{x}$ 的图象与边 $A C$ 交于点E，直线EF分别与y轴和x轴相交于点D和G．给出下列命题：①若 $k = 6$ ，则 $△ O E F$ 的面积为 $\frac{9}{2}$ ；②若 $k = \frac{21}{8}$ ，则点C关于直线EF的对称点在x轴上；③满足题设的k的取值范围是 $0 ＜ k \leq 12$ ；④若 $D E \cdot E G = \frac{25}{6}$ ，则 $k = 2$ ；其中正确的命题个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共6个小题，每小题3分，共18分。

11. 一次函数y=(m+1)x-2m+3的图象一定经过第象限.

查看试题解析
12. 设直线 $y = k x + k (k > 0)$ 与双曲线 $y = \frac{2}{x}$ 分别交于点 $M$ 、点 $N$ ．若 $M N = k + 3$ ，则 $k$ 的值为．

查看试题解析
13. 如图，已知点A（-2，3)，B（2，1)，当直线y= kx-k与线段AB有交点时，k的取值范围是 .

查看试题解析
14. 如图，在平面直角坐标系中，正方形ABCD 的顶点A 的坐标为(-1，1)，点B 在x轴正半轴上，点D 在第三象限的双曲线 $y = \frac{6}{x}$ 上，过点 C 作CE∥x 轴交双曲线于点E，连接BE，则△BCE 的面积为.

查看试题解析
15. 某物流公司的快递车和货车同时从甲地出发，以各自的速度匀速向乙地行驶，快递车到达乙地后卸完物品再另装货物共用45min，立即按原路以另一速度匀速返回，直至与货车相遇.已知货车的速度为60km/h，两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示，现有以下4个结论：
①快递车从甲地到乙地的速度为100km/h；
②甲、乙两地之间的距离为120km；
③图中点B 的坐标为( $3 \frac{3}{4}$ ， 75)；
④快递车从乙地返回时的速度为90km/h.
以上4个结论中正确的是(填序号).

查看试题解析
16. 如图，在平面直角坐标系中，A、B两点在反比例函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象上，延长AB交 $x$ 轴于点 $C$ ，且 $A B = B C, D$ 是第二象限一点，且 $D O / / A B$ ，若 $△ A D C$ 的面积是12，则 $k$ 的值为．

查看试题解析

三、解答题：本大题共10个小题，共102分。

17. 已知点P(a-1， 6+2a) ，解答下列各题：

(1)、若点 P在x轴上，求点 P 的坐标；

(2)、若点Q (5， 8) ，且PQ∥y轴，求点P 的坐标.

查看试题解析
18. 已知y是x的一次函数，且当x=1时，y的值是2，当x=2时，y的值是3，

(1)、求y关于x的函数表达式；

(2)、当y>3时，求x的取值范围.

查看试题解析
19. 如图，某工程队接受一项开挖水渠的工程，所需天数y（单位：天）是每天完成的工程量x（单位：m/天）的反比例函数，其图象经过点（24，50）.

(1)、求y与x的函数关系式；

(2)、已知该工程队每台挖掘机每天能够开挖水渠16m，若要求该工程队恰好15天完成此项任务，那么需要几台这样的挖掘机？

查看试题解析
20. 小王驾驶汽车从甲地走高速公路前往乙地办事，以80千米/小时的平均速度用6小时到达目的地，之后他按原路返回甲地．

(1)、求行驶时间 $t$ （小时）与汽车的平均速度 $v$ （千米/小时）之间的函数关系式；

(2)、根据规定：在高速公路上行驶时，最高车速不得超过120千米/小时，最低车速不得低于60千米/小时．求小王返程行驶时间的取值范围．

查看试题解析
21. 一次函数 $y = k x + 5$ (k为常数)，且 $k \neq 0$ .

(1)、若点(-1，4)在一次函数的图象上，求一次函数的解析式.

(2)、当 $- 3 \leq x \leq - 1$ 时，一次函数 $y = k x + 5$ (k 为常数，且 $k \neq 0$ )有最大值 k，求 k 的值.

(3)、若一次函数 $y = k x + 5$ (k 为常数，且 $k \neq 0$ )与 x 轴的交点为(m，0)，且 $1 \leq k \leq 4$ ，设 $P = 5 m - 3$ ，求 P 的取值范围.

查看试题解析

22.

拟定游玩计划

信息1：某风景区的游览地图如图1所示。

信息2：景区内有一辆免费的电动观光车，匀速地在古刹和飞瀑之间不间断地来回载客（上下车时间忽略不计），首趟观光车于早上9：00从古刹出发。

信息3：小聪在景点古刹游玩结束后，恰好坐上首趟观光车前往塔林。在塔林游玩若干时间后，再坐上第二趟观光车去草甸游玩，小聪和观光车离古刹的路程s（m）与时间t（min）的函数关系如图2所示。

信息4：小聪在飞瀑游玩后，要在中午12：00前赶回古刹吃中饭。

(1)、任务1：确定车速：根据游览地图和函数图象，计算出电动观光车的车速。

(2)、任务2：探究时间：求出小聪到达草甸的具体时间。

(3)、任务3：拟定计划：请为小聪拟定在草甸、飞瀑这两个景点游玩的最长时间及搭乘的车次。

查看试题解析

23. 如图，直线 $y = - 3 x + 6$ 与 $x$ 轴， $y$ 轴分别交于点 $A$ ， $B$ ，在线段 $O B$ 上取一点 $C$ ，连结 $A C$ ，若 $△ A B C$ 的面积为3，求直线 $A C$ 的解析式．

查看试题解析
24. 如图，已知点 $A (1, m)$ 、 $B (n, 1)$ 在反比例函数 $y = \frac{3}{x} (x > 0)$ 的图象上，过点 $A$ 的一次函数 $y = k x + b$ 的图象与 $y$ 轴交于点 $C (0, 1)$ ．

(1)、求 $m$ 、 $n$ 的值和一次函数的表达式；

(2)、连接 $A B$ ，求点 $C$ 到线段 $A B$ 的距离．

查看试题解析
25. 如图1，大约在两千五百年前，墨子和他的学生做了世界上第1个小孔成像的实验，并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”．如图2，根据小孔成像的科学原理，当小孔到像的距离和蜡烛火焰高度不变时，火焰的像高 $y cm$ 是小孔到蜡烛的距离 $x cm$ 的反比例函数．当 $x = 2 cm$ 时， $y = 3 cm$ ．

(1)、求 $y$ 关于 $x$ 的函数表达式；

(2)、在平面直角坐标系中，画出函数图象；

(3)、若小孔到蜡烛的距离为 $5 cm$ 时，求火焰的像高．

查看试题解析
26. 【了解概念】对于给定的一次函数y=kx+b（其中k，b为常数，且k≠0），称函数 $y = {\begin{array}{l} - k x + b (x \geq 0) \\ k x + b (x ≺ 0) \end{array}$ 为一次函数y=kx+b的关联函数.
【理解运用】

(1)、例如：一次函数y=-3x-1的关联函数为 $y = {\begin{matrix} 3 x - 1 (x \geq 0) \\ - 3 x - 1 (x < 0) \end{matrix}$
若点P（2，m）在一次函数y=-3x-1的关联函数的图象上，则m的值为.

(2)、已知一次函数y=-3x-1，我们可以根据学习函数的经验，对它的关联函数 $y = {\begin{matrix} 3 x - 1 (x \geq 0) \\ - 3 x - 1 (x < 0) \end{matrix}$ 的图象与性质进行探究.下面是嘉嘉的探究过程：
①填表：
x
...
-1
0
1
2
...
y
... ...
②根据①中的结果，请在所给的平面直角坐标系中画出一次函数y=-3x-1的关联函数的图象；
③若-1≤x≤2，则y的取值范围为 ▲ .

查看试题解析

x	...	-1	0	1	2	...
y	...					...

华东师大版数学八（下）第16章 函数及其图象 单元测试培优卷

一、选择题：本大题共10个小题，每小题3分，共30分。

二、填空题：本大题共6个小题，每小题3分，共18分。

三、解答题：本大题共10个小题，共102分。

华东师大版数学八（下）第16章函数及其图象单元测试培优卷