人教版八年级下数学进阶测试 20.2 勾股定理的逆定理及其应用 (三阶)
试卷更新日期:2026-02-03 类型:同步测试
一、选择题
-
1. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A、2,3,4 B、1,2,5 C、4,4,4 D、6,8,102. 如图,在小正方形组成的3×2网格中,每个小正方形的顶点称为格点.点A,B,C,D,M,N均在格点上,其中能与点M,N构成一个直角三角形的是 ( )
 A、点A B、点B C、点C D、点 D3. 下列各组数据中,是勾股数的是( )A、 B、9,40,41 C、0.7,2.4,2.5 D、32 , 42 , 524. 下列命题的逆命题不成立的是( )A、等边对等角 B、直角三角形两条直角边的平方和等于斜边的平方 C、两直线平行,内错角相等 D、如果两个实数都是正数,那么它们的积是正数5. 如图,三个正方形的面积分别为 , , , 且K是中点.若 , , , 则的长为( )
A、点A B、点B C、点C D、点 D3. 下列各组数据中,是勾股数的是( )A、 B、9,40,41 C、0.7,2.4,2.5 D、32 , 42 , 524. 下列命题的逆命题不成立的是( )A、等边对等角 B、直角三角形两条直角边的平方和等于斜边的平方 C、两直线平行,内错角相等 D、如果两个实数都是正数,那么它们的积是正数5. 如图,三个正方形的面积分别为 , , , 且K是中点.若 , , , 则的长为( ) A、 B、 C、 D、56. 如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边和的长,再测量点和点之间的距离,由此可推断出是不是直角.这样做的依据是( )
A、 B、 C、 D、56. 如图,小红家的木门左下角有一点受潮,她想检测门是否变形,准备采用如下方法:先测量门的边和的长,再测量点和点之间的距离,由此可推断出是不是直角.这样做的依据是( ) A、勾股定理 B、勾股定理的逆定理 C、三角形内角和定理 D、直角三角形的两锐角互余7. 九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A、勾股定理 B、勾股定理的逆定理 C、三角形内角和定理 D、直角三角形的两锐角互余7. 九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )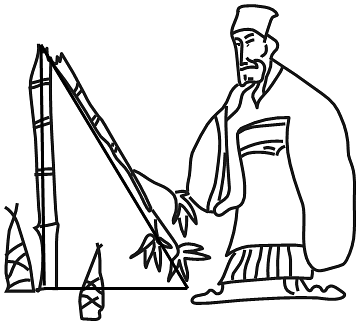 A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺8. 如图:在 中, , 于点D,点P在线段DB上,点M是边AC的中点,连结MP,作 ,点Q在边BC上.若 ,则( )
A、4.55尺 B、5.45尺 C、4.2尺 D、5.8尺8. 如图:在 中, , 于点D,点P在线段DB上,点M是边AC的中点,连结MP,作 ,点Q在边BC上.若 ,则( )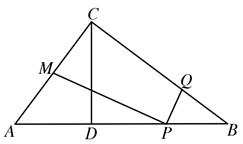 A、当 时,点P与点D重合 B、当 时, C、当 时, D、当 时,
A、当 时,点P与点D重合 B、当 时, C、当 时, D、当 时,二、填空题
-
9. 如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S= .
 10. 如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .
10. 如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .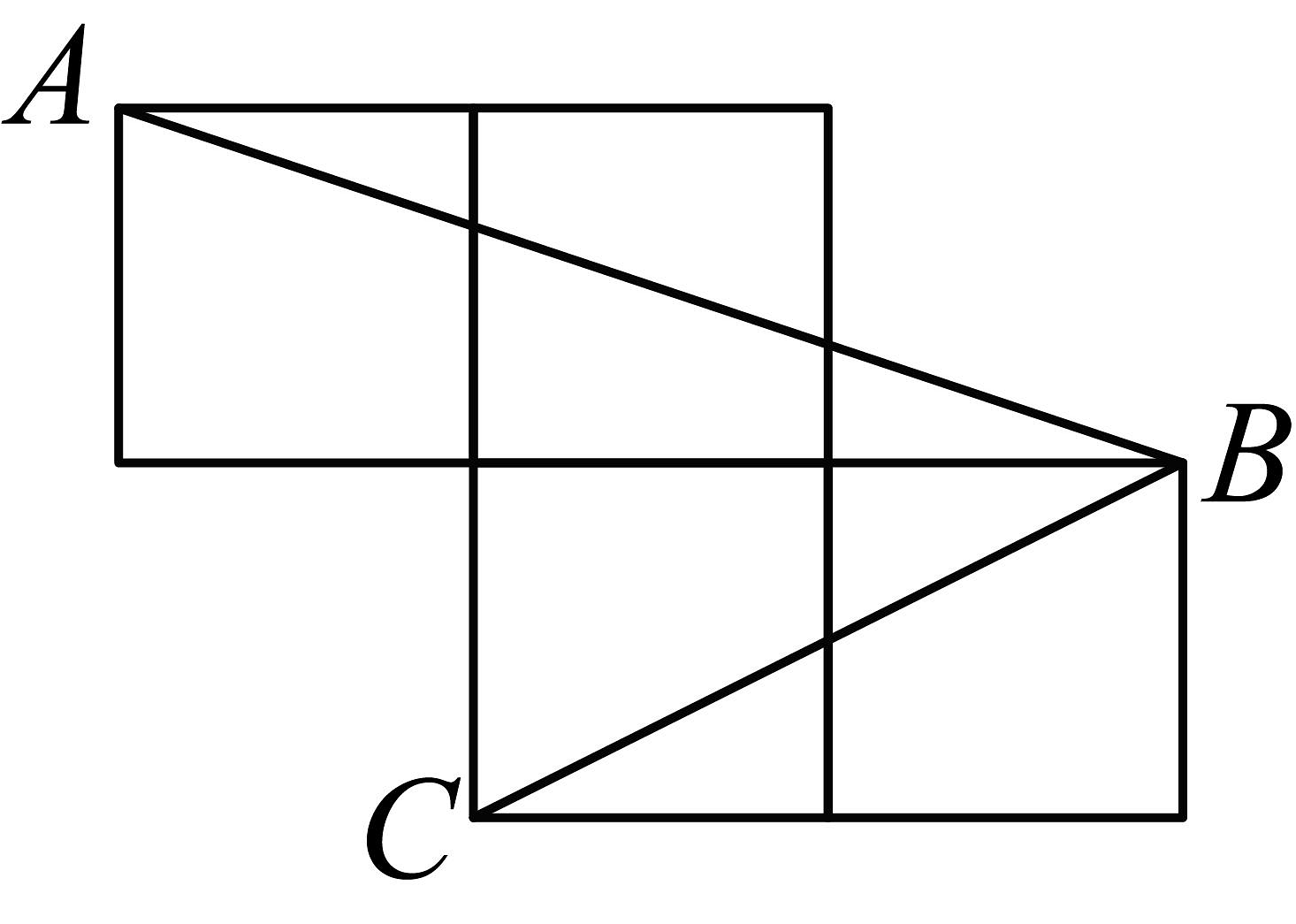 11. 如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入元.
11. 如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入元.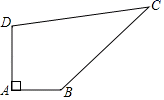 12. 已知,a , b , c是△ABC的三条边长,记 , 其中k为整数.(1)、若三角形为等边三角形,则t= ;(2)、下列结论正确的是 .(写出所有正确的结论)
12. 已知,a , b , c是△ABC的三条边长,记 , 其中k为整数.(1)、若三角形为等边三角形,则t= ;(2)、下列结论正确的是 .(写出所有正确的结论)①若k=2,t=1,则△ABC为直角三角形;
②若 , 则5<t<11;
③若 , a , b , c为三个连续整数,且a<b<c , 则满足条件的△ABC的个数为7.
三、解答题
-
13. 如图1,在平面直角坐标系中,已知点A的坐标为 , , , 点B在第一象限内,且满足 .
 (1)、试判断的形状,并说明理由;(2)、在第二象限内是否存在一点P,使得是以为腰的等腰直角三角形,若存在,求出点P的坐标;若不存在,请说明理由;(3)、如图2,点C为线段上一动点,点D为线段上一动点,且始终满足 . 求的最小值.14. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
(1)、试判断的形状,并说明理由;(2)、在第二象限内是否存在一点P,使得是以为腰的等腰直角三角形,若存在,求出点P的坐标;若不存在,请说明理由;(3)、如图2,点C为线段上一动点,点D为线段上一动点,且始终满足 . 求的最小值.14. 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ. (1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、已知PA=3,PB=4,PC=5,连结PQ.判断△PQC的形状,并说明理由.15. 今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)、观察并猜想AP与CQ之间的大小关系,并说明理由.(2)、已知PA=3,PB=4,PC=5,连结PQ.判断△PQC的形状,并说明理由.15. 今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响. (1)、海港C受台风影响吗?为什么?(2)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?16. 如图,在四边形中,已知 , , , , .
(1)、海港C受台风影响吗?为什么?(2)、若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?16. 如图,在四边形中,已知 , , , , . (1)、判断是直角三角形吗?请说明理由.(2)、连接 , 求的面积.17. 如图,在6×6的正方形网格中,四边形ABCD的顶点均在格点上,按下列要求作图。
(1)、判断是直角三角形吗?请说明理由.(2)、连接 , 求的面积.17. 如图,在6×6的正方形网格中,四边形ABCD的顶点均在格点上,按下列要求作图。 (1)、如图①,在BC上找一格点E,连结AE,DE,使得△ADE为直角三角形。(2)、如图②,F为BC的中点,请在网格中找一格点G,作直线FG,使得FG平分四边形ABCD的面积。18. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等.①分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫作分组分解法.
(1)、如图①,在BC上找一格点E,连结AE,DE,使得△ADE为直角三角形。(2)、如图②,F为BC的中点,请在网格中找一格点G,作直线FG,使得FG平分四边形ABCD的面积。18. 我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、添项拆项法、十字相乘法等等.①分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫作分组分解法.例如:
②十字相乘法:十字相乘法能用于二次三项式的分解因式.
分解步骤:1.分解二次项,所得结果分别写在十字交叉线的左上角和左下角;2.分解常数项,所得结果分别写在十字交叉线的右上角和右下角;3.交叉相乘,求代数和,使其等于一次项;4.观察得出原二次三项式的两个因式,并表示出分解结果.这种分解方法叫作十字相乘法.
例如: 分析:
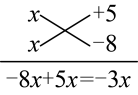
观察得出:两个因式分别为与
解:原式
③添项拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法叫作拆项法.
例如: .
(1)、仿照以上方法,按照要求分解因式:①(分组分解法);
②(十字相乘法);
(2)、已知:a、b、c为的三条边, , 判断的形状.19. 定义:如图,点M,N把线段AB分割成AM.MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)已知M、N线段AB分割成AM,MN,NB,若 , 则点M,N是线段AB的勾股分割点吗?请说明理由;
(2)已知点M、N是线段AB的勾股分割点,且AM为直角边,若 , 求BN的长.
20. 在数学活动课上,同学们用边长为 , 的两个正方形 , (如图1)进行摆放,其中 . 现有两种摆放方式:方式一,如图2,将正方形放在正方形内部;方式二,如图3,将正方形 , 并列放置在边长为的正方形内部.若记图1中正方形 , 的面积之和为 , 记图2,图3中阴影部分的面积分别为 , , 解答下列问题: (1)、用 , 的代数式表示;(2)、若的三边长分别为 , , . 试猜想是哪一类三角形,并证明你的猜想;(3)、已知直角三角形的两边长为 , , 且 , 为整数,当时,求直角三角形第三边的长.
(1)、用 , 的代数式表示;(2)、若的三边长分别为 , , . 试猜想是哪一类三角形,并证明你的猜想;(3)、已知直角三角形的两边长为 , , 且 , 为整数,当时,求直角三角形第三边的长.