人教版八年级下数学进阶测试 20.1 勾股定理及其应用（三阶）

试卷更新日期：2026-02-03 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在 $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于点 $D$ ，点 $E$ 在边 $A B$ 上， $A E = B E = B D$ ， $D E = \frac{2}{3}$ ，则 $A D$ 的长度为（）

A、 $\sqrt{2}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析
2. 如图，桌上有一个圆柱形无盖玻璃杯，高6厘米，底面周长为 16厘米，在杯口内壁离杯口1.5厘米的A处有一滴蜜糖，在玻璃杯的外壁与A相对的点 P 处有一只小虫，小虫离杯底的距离为1.5厘米，则小虫爬到蜜糖 A 处的最短路程是( )

A、 $\sqrt{73}$ 厘米 B、10厘米 C、8 $\sqrt{2}$ 厘米 D、8厘米

查看试题解析
3. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形，如图所示，已知∠A=90°，BD=4，CF=6，设正方形ADOF的边长为x，则 $x^{2} + 10 x =$ ( )

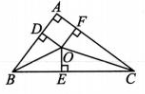A、12 B、16 C、20 D、24

查看试题解析
4. 如图，在 $△ A B C$ 中，P为平面内的一点，连接 $A P 、 P B 、 P C$ ，若 $∠ A C B = 30 ° ， A C = 8 ， B C = 10$ ，则 $4 P A + 2 P B + 2 \sqrt{3} P C$ 的最小值是（）

A、 $4 \sqrt{89}$ B、36 C、 $4 \sqrt{10} + 2 \sqrt{5} + 6 \sqrt{7}$ D、 $16 \sqrt{10} - 10$

查看试题解析
5. 将一个等腰三角形 $A B C$ 纸板沿垂线段 $A D ， D E$ 进行剪切，得到三角形①②③，再按如图2方式拼放，其中 $E C$ 与 $B D$ 共线．若 $B D = 10$ ，则 $A B$ 的长为（　　）

A、 $\frac{32}{3}$ B、 $\frac{25}{2}$ C、10 D、 $\sqrt{70}$

查看试题解析
6. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以该三角形的三条边为边向外作正方形 $A B E F$ ，正方形 $B C G H$ 和正方形 $A C M N$ ，给出下列结论： $① A B = M G . ② S_{△ A B C} = S_{△ A F N} . ③$ 过点 $B$ 作 $B I ⊥ E H$ 于点 $I$ ，延长 $I B$ 交 $A C$ 于点 $J$ ，则 $A J = C J . ④$ 若 $A B = 2$ ，则 $E H^{2} + F N^{2} = 20 .$ 其中正确的结论个数是( )

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

7. 在△ABC中，∠CAB＝30°，∠ABC＝45°，AC＝2．D为直线AB上一点，以CD为边在CD右侧作等边△CDE ，连接BE ．当△BDE为等腰三角形时，则AD的长为．

查看试题解析
8. 如图，AD∥BC，∠B=90°，∠C=60°，BC=2AD=4，点M为BC的中点，点E，F在边AB，CD上运动，点 P 在线段 MC 上运动，连接EF，EP，PF，则△EFP周长的最小值为.

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C = 5, B C = 6, D$ 是BC的中点， $E$ 是边AB上的一点，点 $B$ 与点 $B$ ＇关于直线DE对称，点 $B$ 恰好在边AC上，连结 $B B^{^{'}}$ ，则 $B B^{^{'}}$ 的长是．

查看试题解析
10. 在一次综合实践活动中，小明将6个边长为1的小正方形进行如下操作：第一次操作，三个小正方形一组，边重叠拼接成如图1所示的2个“ $L$ 型”；第二次操作，将这2个“ $L$ 型”顶点 $G$ 、 $J$ 重合，并且使得 $E$ ， $G (J)$ ， $H$ 三点共线，摆放成如图2所示的图形；第三次操作，将图2中的新图形放置在长方形纸片 $A B C D$ 中，此时发现，小正方形的顶点 $E$ 、 $F$ 、 $H$ 、 $I$ 都落在长方形 $A B C D$ 的各边上，若 $A B = 3$ ，则 $B C =$ ．

查看试题解析

三、解答题

11. 如图，有人在岸上点 $C$ 的地方，用绳子拉船靠岸，开始时，绳长 $C B = 25$ 米， $C A ⊥ A B$ 且 $C A = 15$ 米，拉动绳子将船从点 $B$ 沿 $B A$ 方向行驶到点 $D$ 后，绳长 $C D = 15 \sqrt{2}$ 米．

(1)、试判定 $Δ A C D$ 的形状，并说明理由；

(2)、求船体移动距离 $B D$ 的长度．

(3)、若在BD段拉动船的速度为1米/秒，到达D后增加了人力，拉动船的速度变为2米/秒，求把船从B拉到岸边A点所用时间．

查看试题解析
12. 某校八（1）班的小华和小轩学习了“勾股定理”之后，为了测得风筝的垂直高度 $C E$ ，他们进行了如下操作：
①测得水平距离 $B D$ 的长为12米；
②根据手中剩余线的长度计算出风筝线 $B C$ 的长为20米；
③牵线放风筝的小明的身高为1.62米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果小明想风筝沿 $D C$ 方向再上升4米，则他应该再放出多少米线?（结果保留根号）

查看试题解析
13. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲！如图，“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b，斜边为c．

(1)、请利用“赵爽弦图”证明： $a^{2} + b^{2} = c^{2}$ ；

(2)、若大正方形的面积为20，小正方形面积为4，求其中一个直角三角形的面积．

查看试题解析
14. 勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”（如图1），后人称之为“赵爽弦图”，流传至今．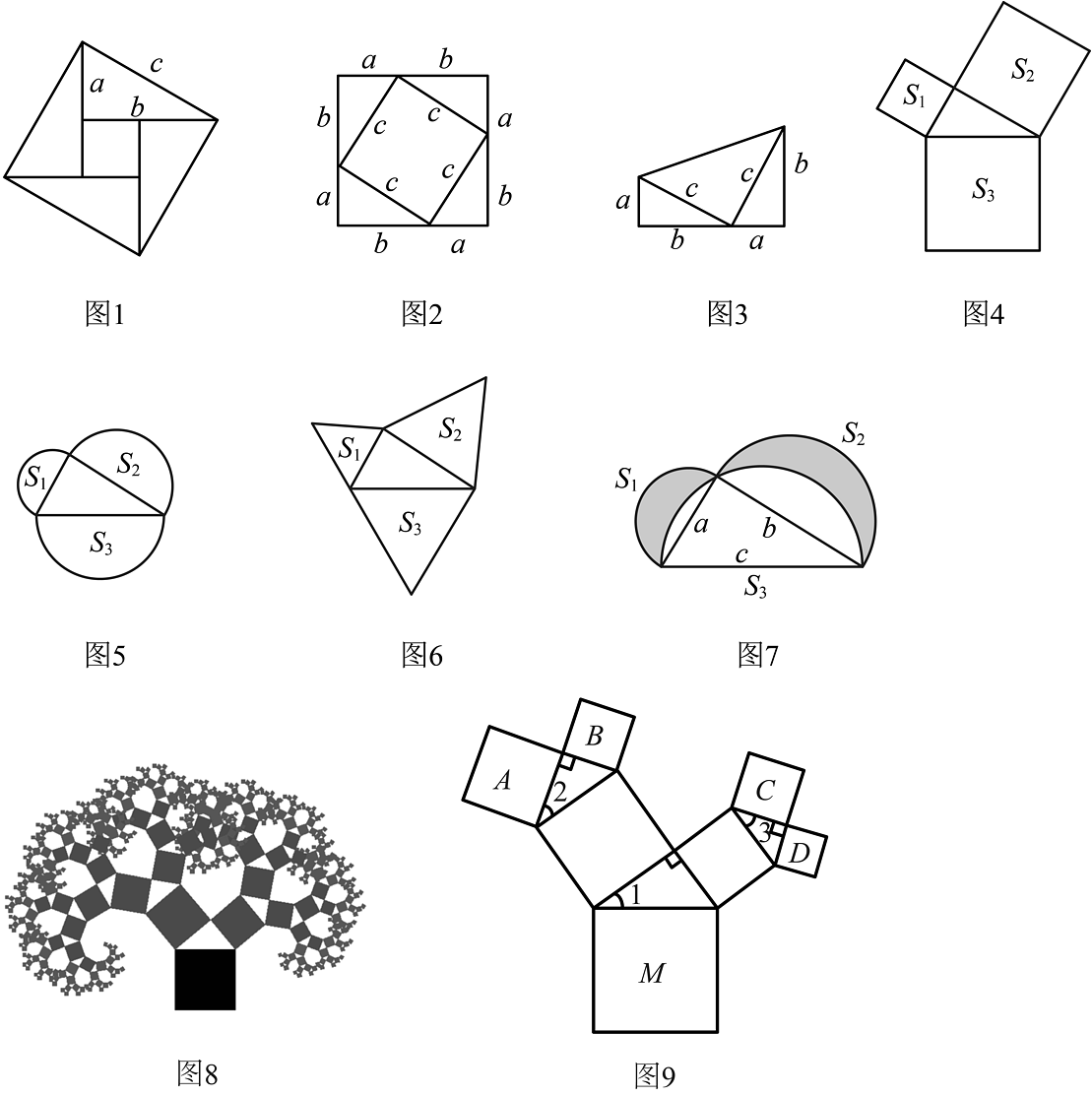

(1)、①如果用a，b和c分别表示直角三角形的两直角边和斜边，则______（用含有a，b和c的式子表示三者之间的等量关系）；
②勾股定理的证明，人们已经找到了400多种方法，请从下列几种常见的证明方法中任选一种来证明该定理；（以下图形均满足证明勾股定理所需的条件）

(2)、①如图4、5、6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足 $S_{1} + S_{2} = S_{3}$ 的有______个；
②如图7所示，分别以直角三角形两直角边为直径作半圆，设图中两个月形图案（图中阴影部分）的面积分别为 $S_{1}$ ， $S_{2}$ ，直角三角形面积为 $S_{3}$ ，请判断 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 的关系并证明；

(3)、如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图8所示的“勾股树”．在如图9所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，已知 $∠ 1 = ∠ 2 = ∠ 3 = ∠ α$ ，则当 $∠ α$ 变化时，回答下列问题：（结果可用含m的式子表示）则：
① $a^{2} + b^{2} + c^{2} + d^{2} =$ ______．
②b与c的关系为______，a与d的关系为______．

查看试题解析
15. 【阅读理解】在数学学习中，我们常常借助由边长为1的小正方形组成的网格来解决问题，并把由格点（小正方形的顶点）组成的正方形称为格点正方形，图①是由四个边长为1的小正方形组成的网格，容易发现格点正方形 $A B C D$ 的面积为2，则这个格点正方形的边长为 $\sqrt{2}$ ．
【问题解决】

(1)、图②是由9个小正方形网格组成的图形，那么格点正方形 $E F G H$ 的边 $E H =$ ．

(2)、在由16个小正方形网格组成的图③中，画出边长为 $\sqrt{8}$ 的格点正方形．

(3)、若 $a$ 是 $\sqrt{8}$ 的整数部分， $b$ 是 $\sqrt{8}$ 的小数部分，求 ${(a - b)}^{- 2}$ 的值．

查看试题解析
16. 如图1，在△ABC中， AB=AC， BD 是边AC上的高线， CD=1， AD=4.

(1)、求AB， BC的长.

(2)、若P 是射线DA上的一动点，作 PE⊥BC于点E，连结DE，
①如图2，当点 P在线段AD上时，若△CDE 是等腰三角形，求DP 的长度；
②设直线 PE交直线AB于点 F，连结 DF， BP，若 $S_{△ D A F :} S_{△ D B A} = 3 : 5,$ 则BP长为 (直接写出结果).

查看试题解析

人教版八年级下数学进阶测试 20.1 勾股定理及其应用 （三阶）

一、选择题

二、填空题

三、解答题

人教版八年级下数学进阶测试 20.1 勾股定理及其应用（三阶）