湖南省长沙市雅礼实验中学等六校联考2025-2026学年七年级上学期数学期末样卷

试卷更新日期：2026-01-26 类型：期末考试

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分．在每小题给出的选项中，只有一项是符合题目要求的．

1. 地球上的海洋面积约为362000000km² ，用科学记数法将362000000表示为( )

A、 $36.2 \times 1 0^{7}$ B、 $3.62 \times 1 0^{7}$ C、 $3.62 \times 1 0^{8}$ D、 $0.362 \times 1 0^{9}$

查看试题解析
2. 下列四个立体图形的展开图中，是圆锥展开图的为( )

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、 $- a - a = 0$ B、 $- (x - y) = - x + y$ C、 $2 (b - 3 a) = 2 b - 3 a$ D、 $8 a^{4} - 2 a^{2} = 6 a^{2}$

查看试题解析
4. 下列叙述中，正确的是（　　）

A、单项式 $x^{2} y$ 的系数是 $0$ ，次数是 $3$ B、多项式 $3 a^{3} b + 2 a^{2} + 1$ 是六次三项式 C、多项式 $x^{2} - 2 x - 1$ 的常数项是 $- 1$ D、 $0$ 不是整式

查看试题解析
5. 方程2x-1=3的解为（）

A、x=-1 B、x=-2 C、x=1 D、x=2

查看试题解析
6. 如图，在 $△ A B C$ 中，点D，E，F分别在边 $B C$ ， $A B$ ， $A C$ 上，下列不能判定 $D E ∥ A C$ 的条件是（）

A、 $∠ 3 = ∠ C$ B、 $∠ 1 + ∠ 4 = 180 °$ C、 $∠ 1 = ∠ A F E$ D、 $∠ 1 + ∠ 2 = 180 °$

查看试题解析
7. 把一些图书分给某班学生阅读，若每人分3本，则剩余20本；若每人分4本，则缺25本．设这个班有学生x人，则可以列方程为（）

A、 $3 x - 20 = 4 x + 25$ B、 $3 x + 20 = 4 x - 25$ C、 $\frac{x + 20}{3} = \frac{x - 25}{4}$ D、 $\frac{x}{3} + 20 = \frac{x}{4} - 25$

查看试题解析
8. 下列命题中，是真命题的有（     ）
①对顶角相等；             ②不相交的两条直线一定平行；
③等角的补角相等；       ④如果 $|a| > |b|$ ，那么 $a > b$

A、①和② B、①和③ C、②和③ D、③和④

查看试题解析
9. 如图，射线OA表示北偏东30°方向，射线OB表示北偏西50°方向，则∠AOB的度数是（）

A、60° B、80° C、90° D、100°

查看试题解析
10. 若实数a，b在数轴上的对应点如图，则化简 $\sqrt{a^{2} - 2 a b + b^{2}} + | a + b |$ 的结果为（）

A、 $2 a$ B、 $2 b$ C、 $- 2 a$ D、 $- 2 b$

查看试题解析

二、填空题：本题共6小题，每小题3分，共18分．

11. 若盈余3万元记作 $+ 3$ 万元，则亏损2万元记作万元.

查看试题解析
12. 下列语句：
①绝对值是它本身的数是正数；
② $- (- 5)$ 表示 $- 5$ 的相反数；
③除以一个不为0的数，等于乘这个数的倒数；
④单项式 $\frac{2 a^{3} b}{3}$ 的系数是2；
⑤ $x^{3}$ 与 $4^{3}$ 不是同类项．
其中正确语句是．（填序号）

查看试题解析
13. 若 $a$ 、 $b$ 互为相反数，c、d互为倒数，则 ${(a + b)}^{2} - 2 c d$ ＝．

查看试题解析
14. 一个锐角的补角比它的余角的2倍多 $36 °$ ，则这个锐角度数为 $°$ ．

查看试题解析
15. 如图，在 $R t$ △ $O A B$ 中， $∠ A O B = 30 °$ ，将△ $O A B$ 绕点 $O$ 逆时针旋转 $100 °$ 得到△ $O A_{1} B_{1}$ （A、 $B$ 分别与 $A_{1}$ 、 $B_{1}$ 对应），则 $∠ A_{1} O B$ 的度数为度．

查看试题解析
16. 一元二次方程x²=4x的解是.

查看试题解析

三、解答题：本题共9小题，共72分．解答应写出文字说明，证明过程或演算步骤．

17. 计算：
① $- 3 + 1 - (- 5)$ ；
② $(- 3 \frac{3}{7}) + 12.5 + (- 16 \frac{4}{7}) - (- 2.5)$ ；
③ $- 2^{2} \times 5 - {(- 2)}^{3} \div 4 - | - 2 |$ ；
④ $(- \frac{7}{12} + \frac{1}{2} - \frac{5}{6}) \times (- 36)$ .

查看试题解析
18. 解下列一元一次方程．

(1)、 $2 + 2 x = x - 3$

(2)、 $\frac{5 x - 3}{4} - \frac{7 x + 5}{6} = 3$

查看试题解析
19. 先化简，再求值， $2 (a^{2} b + \frac{1}{2} a b^{2}) - 3 (a^{2} b - 1) - 2 a b^{2} - 1$ ，其中 $a = - \frac{1}{3}$ ， $b = 3$ ．

查看试题解析
20. 已知 $a$ ， $b$ 互为相反数， $c$ 和 $d$ 互为倒数， $m$ 的绝对值为 $2$ ，求 $\frac{2024 {(a + b)}^{2}}{2025} - m^{2} + 3 c d$ ．

查看试题解析
21. 如图，已知 $A$ 、 $B$ 、 $C$ 、 $D$ 四点，请按要求作图，并解答．

(1)、画直线 $A B$ ；

(2)、画射线 $D B$ ；

(3)、连接 $A C$ 与射线 $D B$ 交于点 $P$ ；

(4)、若点 $M$ 是线段 $B D$ 的中点， $B P = 3$ ， $D P = 7$ ，求线段MP的长．

查看试题解析
22. 学校实验室需要向某工厂定制一批三条腿的桌子，已知该工厂有24名工人，每人每天可以生产20块桌面或者300条桌腿，1块桌面需要配3条桌腿，为了使每天生产的桌面和桌腿刚好配套，则应该安排多少人生产桌面，多少人生产桌腿？

查看试题解析
23. 如图，点D，E分别在△ABC的边AB，AC上，点F在线段BE上，且∠EDF=∠C，DE//BC.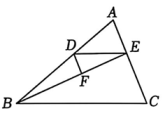

(1)、判断DF与AC的位置关系，并说明理由；

(2)、若DF平分∠BDE，∠ADE=38°，求∠AED.

查看试题解析
24. 定义：如果两个一元一次方程的解互为相反数，我们就称这两个方程为“和谐方程”．
例如：方程 $2 x = 4$ 和 $x + 2 = 0$ 为“和谐方程”．

(1)、若关于 $x$ 的方程 $3 x + m = 0$ 与方程 $4 x - 2 = x + 10$ 是“和谐方程”，求 $m$ 的值；

(2)、若“和谐方程”的两个解的差为4，其中一个解为 $n$ ，求 $n$ 的值；

(3)、若无论 $m$ 取任何有理数，关于 $x$ 的方程 $\frac{2 x + m a}{3} = \frac{b}{2} + m$ （ $a$ ， $b$ 为常数）与关于 $y$ 的方程 $y + 1 = 2 y - 2$ 都是“和谐方程”，求 $a b$ 的值．

查看试题解析
25. 已知数轴上 $A$ ， $B$ 两点对应的数分别为 $a$ ， $b$ ，且 $a$ ， $b$ 满足 $|a + 20| = - {(b - 13)}^{2}$ ，点 $C$ 对应的数为 $16$ ，点 $D$ 对应的数为 $- 13$ ．

(1)、求 $a$ ， $b$ 的值；

(2)、点 $A$ ， $B$ 沿数轴同时出发相向匀速运动，点 $A$ 的速度为 $6$ 个单位 $/$ 秒，点 $B$ 的速度为 $2$ 个单位 $/$ 秒，若 $t$ 秒时点 $A$ 到原点的距离和点 $B$ 到原点的距离相等，求 $t$ 的值；

(3)、在（2）的条件下，点 $A$ ， $B$ 从起始位置同时出发．当 $A$ 点运动到点 $C$ 时，迅速以原来的速度返回，到达出发点后，又折返向点 $C$ 运动． $B$ 点运动至 $D$ 点后停止运动，当 $B$ 停止运动时点 $A$ 也停止运动．求在此过程中， $A$ ， $B$ 两点同时到达的点在数轴上对应的数．

查看试题解析