湘教版数学八年级下册 1.7 正方形 同步分层练习
试卷更新日期:2026-01-22 类型:同步测试
一、夯实基础
-
1. 矩形、正方形、菱形都具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线长度相等 D、一组对角线平分一组对角2. 下列四边形:①正方形,②矩形,③菱形,④平行四边形.对角线一定相等的是( )A、①②④ B、①③④ C、①② D、②③3. 如图,点在正方形的内部,且是等边三角形,连接 , , 则( )
 A、 B、 C、 D、4. 如图,正方形的边长为 , 过线段上的两点分别作和的垂线,则阴影部分的面积为( ) .
A、 B、 C、 D、4. 如图,正方形的边长为 , 过线段上的两点分别作和的垂线,则阴影部分的面积为( ) . A、 B、 C、 D、5. 下列条件可以利用定义说明平行四边形是正方形的是( )A、 B、 C、 D、以上均错6. 正方形是轴对称图形,它的对称轴有( )A、2条 B、3条 C、4条 D、5条7. “正方形的四条边都相等”的逆命题可以写成 , 该逆命题是命题(填写“真”或“假”).8. 将对角线分别为和的菱形改为一个面积不变的正方形,则正方形的边长为 .9. 如图,在正方形的外侧,作等边 , 则 .
A、 B、 C、 D、5. 下列条件可以利用定义说明平行四边形是正方形的是( )A、 B、 C、 D、以上均错6. 正方形是轴对称图形,它的对称轴有( )A、2条 B、3条 C、4条 D、5条7. “正方形的四条边都相等”的逆命题可以写成 , 该逆命题是命题(填写“真”或“假”).8. 将对角线分别为和的菱形改为一个面积不变的正方形,则正方形的边长为 .9. 如图,在正方形的外侧,作等边 , 则 . 10. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 .
10. 如图,点是正方形的对角线上的一点,于点 , . 则点到直线的距离为 . 11. 如图,在正方形中,是边的中点,是边的中点,连接、 . 求证: .
11. 如图,在正方形中,是边的中点,是边的中点,连接、 . 求证: .
二、能力提升
-
12. 在▱ABCD中,有以下四个条件:①AB=BC;②∠BAD=90°;③AC⊥BD;④AC=BD.现从中任选两个条件作为一个组合,其中不能推出四边形ABCD是正方形的是 ( )A、①② B、①④ C、②④ D、③④13. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm,接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
 A、20cm B、30cm C、40cm D、20cm14. 如图,在正方形外取一点E,连接 . 过点B作交于点P.若 , , 下列结论:
A、20cm B、30cm C、40cm D、20cm14. 如图,在正方形外取一点E,连接 . 过点B作交于点P.若 , , 下列结论: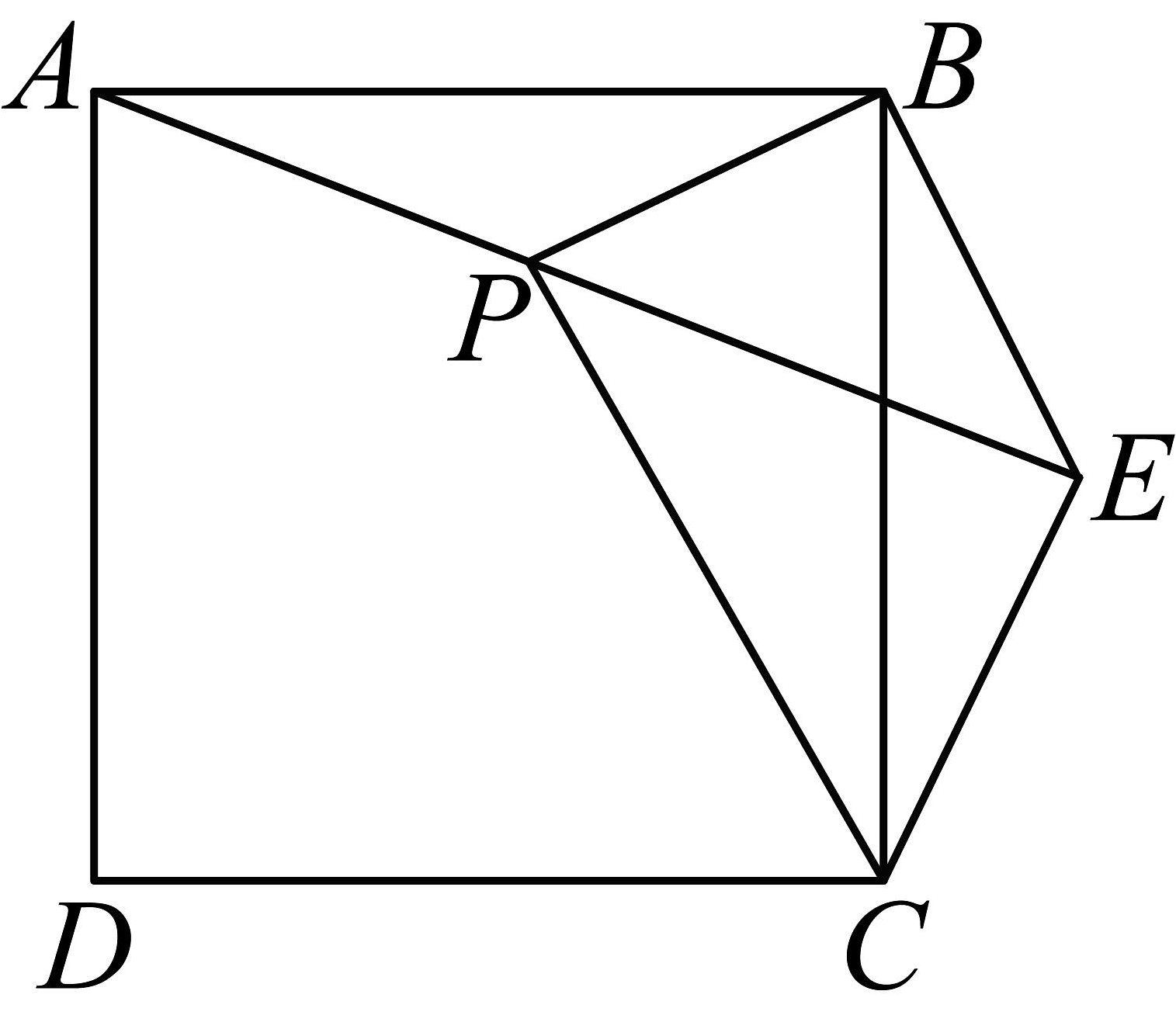
①;②点C到直线的距离为;③P是的中点;④ .
其中正确结论的个数是( )
A、1 B、2 C、3 D、415. 如图,在边长为4的正方形中,点是上一点,点是延长线上一点,连接 , , 平分 . 交于点 . 若 , 则的长度为( ) A、2 B、 C、 D、16. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中正确结论有( )个.
A、2 B、 C、 D、16. 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE , 其中正确结论有( )个. A、2 B、3 C、4 D、517. 如图,正方形和正方形的点在同一条直线上,点为的中点,连接 , 则已知下列哪条线段的长度,一定能求出线段的长( )
A、2 B、3 C、4 D、517. 如图,正方形和正方形的点在同一条直线上,点为的中点,连接 , 则已知下列哪条线段的长度,一定能求出线段的长( ) A、 B、 C、 D、18. 如图,将三张大小相同的透明正方形纸片的一个顶点重合放置,那么的度数为 .
A、 B、 C、 D、18. 如图,将三张大小相同的透明正方形纸片的一个顶点重合放置,那么的度数为 . 19. 如图,已知正方形中, , , 垂直于 , 已知 , 则 .
19. 如图,已知正方形中, , , 垂直于 , 已知 , 则 . 20. 如图,清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形的方法证明了勾股定理,连结 , 若正方形的面积为29, , 则的长为 .
20. 如图,清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形的方法证明了勾股定理,连结 , 若正方形的面积为29, , 则的长为 . 21. 如图,四边形是平行四边形, , , 点E是边的延长线上的动点.连接 . 过点C作于点F.
21. 如图,四边形是平行四边形, , , 点E是边的延长线上的动点.连接 . 过点C作于点F. (1)、求证:四边形是正方形;(2)、当点F是的中点,且时,求四边形的面积.22. 如图所示,在正方形中,点在上,且 .
(1)、求证:四边形是正方形;(2)、当点F是的中点,且时,求四边形的面积.22. 如图所示,在正方形中,点在上,且 . (1)、求证:;(2)、判断四边形的形状并说明理由.
(1)、求证:;(2)、判断四边形的形状并说明理由.三、拓展创新

