湘教版数学八年级下册 1.4 三角形的中位线定理 同步分层练习
试卷更新日期:2026-01-22 类型:同步测试
一、夯实基础
-
1. 如图,在中,DE是的中位线,若DE=3,则的长为( )
 A、6 B、5 C、4 D、32. 如图,是的中位线,若 , 则的长是( )
A、6 B、5 C、4 D、32. 如图,是的中位线,若 , 则的长是( ) A、4 B、5 C、6 D、73. 如图,为了测量池塘边、两点之间的距离,在的同侧取一点 , 连接并延长至点 , 连接并延长至点 , 使得 , . 若测得 , 则 , 间的距离为( )
A、4 B、5 C、6 D、73. 如图,为了测量池塘边、两点之间的距离,在的同侧取一点 , 连接并延长至点 , 连接并延长至点 , 使得 , . 若测得 , 则 , 间的距离为( ) A、13 B、16 C、18 D、204. 三角形的三条中位线的长分别为 , , , 则原三角形的周长为( )A、 B、 C、 D、5. 如图,点D、E分别是 , 的中点, , 则池塘的宽度为( )
A、13 B、16 C、18 D、204. 三角形的三条中位线的长分别为 , , , 则原三角形的周长为( )A、 B、 C、 D、5. 如图,点D、E分别是 , 的中点, , 则池塘的宽度为( ) A、3 B、4 C、5 D、66. 人字梯及其侧面如图所示,AB,AC为支撑架,DE为拉杆,D,E分别是AB,AC的中点,若 , 则B,C两点的距离为cm.
A、3 B、4 C、5 D、66. 人字梯及其侧面如图所示,AB,AC为支撑架,DE为拉杆,D,E分别是AB,AC的中点,若 , 则B,C两点的距离为cm.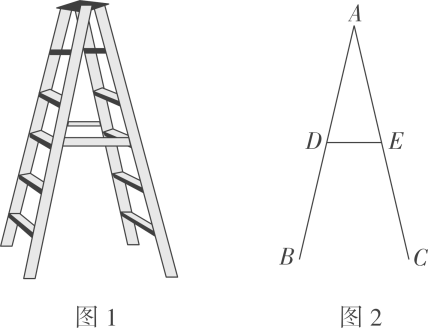 7. 如图,在中, , , , 点分别平分线段 , 则的长为 .
7. 如图,在中, , , , 点分别平分线段 , 则的长为 . 8. 如图,在四边形中, , 为中点,连接交于点 , 若为中点, , , 则 .
8. 如图,在四边形中, , 为中点,连接交于点 , 若为中点, , , 则 . 9. 如图,在中, , , 分别是边 , , 的中点,连接 , , 求证:四边形是平行四边形.
9. 如图,在中, , , 分别是边 , , 的中点,连接 , , 求证:四边形是平行四边形. 10. 在中, , 点D,E分别是的中点,点F在的延长线上,且 . 求证:四边形是平行四边形.
10. 在中, , 点D,E分别是的中点,点F在的延长线上,且 . 求证:四边形是平行四边形.
二、能力提升
-
11. 如图,在中,D是中点,E是中点,则的长等于的( )
 A、两倍 B、一倍 C、一半 D、无法确定12. 如图,DE是△ABC的中位线,直角∠AFB的顶点在DE上,AB=5,BC=8,则EF的长为( )
A、两倍 B、一倍 C、一半 D、无法确定12. 如图,DE是△ABC的中位线,直角∠AFB的顶点在DE上,AB=5,BC=8,则EF的长为( ) A、1 B、1.5 C、2 D、不能确定13. 如图,的面积为 , 点D,E,F分别是 , , 上的三个中点,则的面积是( )
A、1 B、1.5 C、2 D、不能确定13. 如图,的面积为 , 点D,E,F分别是 , , 上的三个中点,则的面积是( )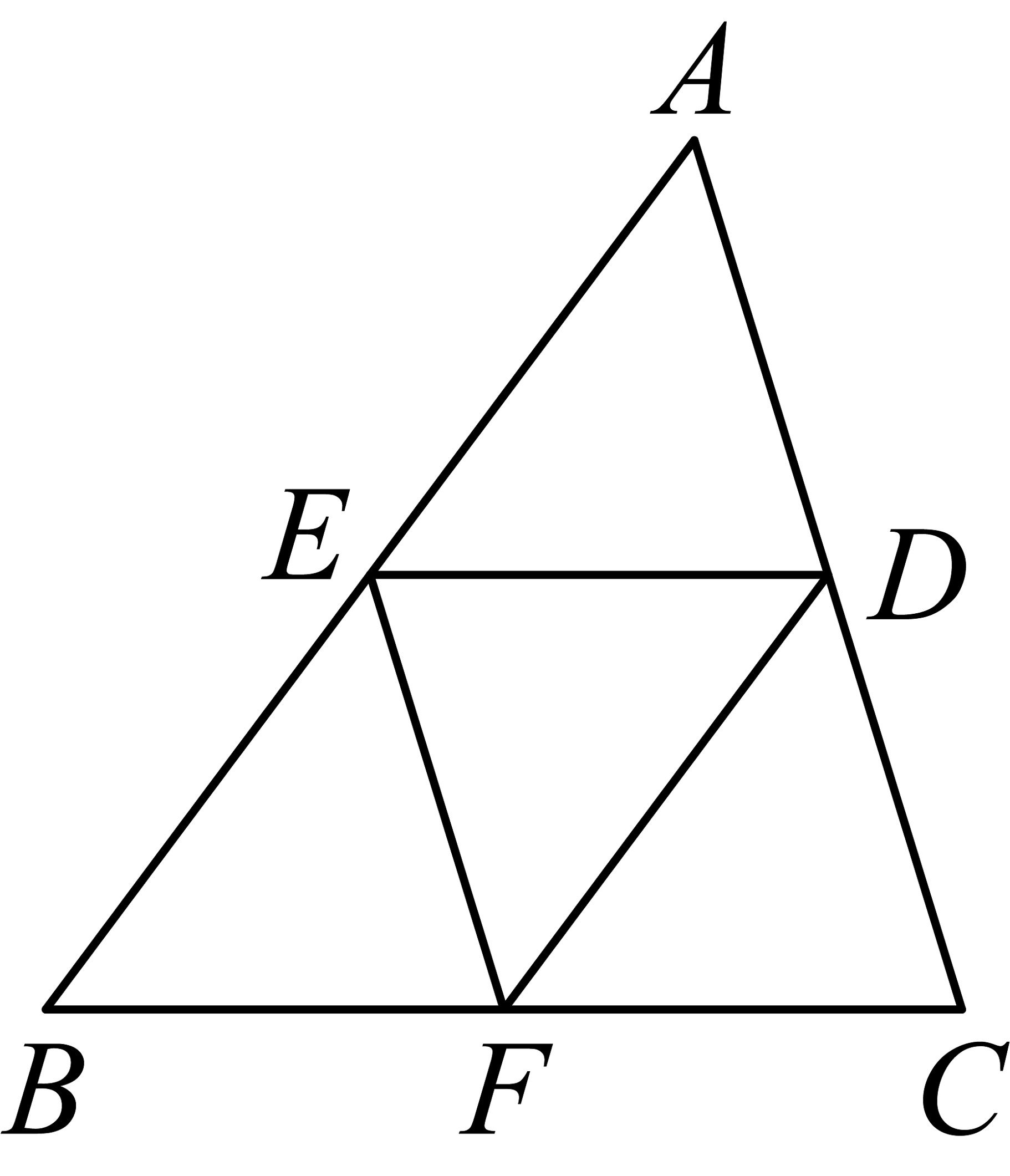 A、 B、 C、 D、14. 如图,四边形中,是中点,、分别是、的中点,当动点在上从向移动时,下列结论成立的是( )
A、 B、 C、 D、14. 如图,四边形中,是中点,、分别是、的中点,当动点在上从向移动时,下列结论成立的是( ) A、线段的长逐渐增大 B、线段的长逐渐减小 C、线段的长不变 D、线段的长与点的位置有关15. 如图,在平行四边形中, , 点E,F分别是 , 的中点,则等于米.
A、线段的长逐渐增大 B、线段的长逐渐减小 C、线段的长不变 D、线段的长与点的位置有关15. 如图,在平行四边形中, , 点E,F分别是 , 的中点,则等于米. 16. 如图,M是的边的中点,平分于点N,且 , 则的周长是 .
16. 如图,M是的边的中点,平分于点N,且 , 则的周长是 . 17. 如图,平行四边形中, , , 点P是边上的点,连接 , 以为对称轴作的轴对称图形 , 连接 , 当点P是线段的中点,且时,则的长为 .
17. 如图,平行四边形中, , , 点P是边上的点,连接 , 以为对称轴作的轴对称图形 , 连接 , 当点P是线段的中点,且时,则的长为 .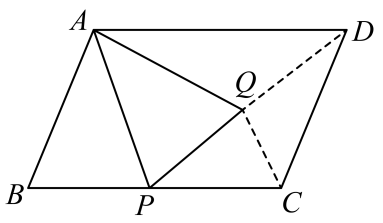 18. 如图,为四边形的对角线,已知 .
18. 如图,为四边形的对角线,已知 . (1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长.19. 如图,在中,点G、H分别是、的中点,点E、F在对角线上,且 .
(1)、求证:四边形是平行四边形.(2)、分别为的中点,连结 . 若 , 求的长.19. 如图,在中,点G、H分别是、的中点,点E、F在对角线上,且 .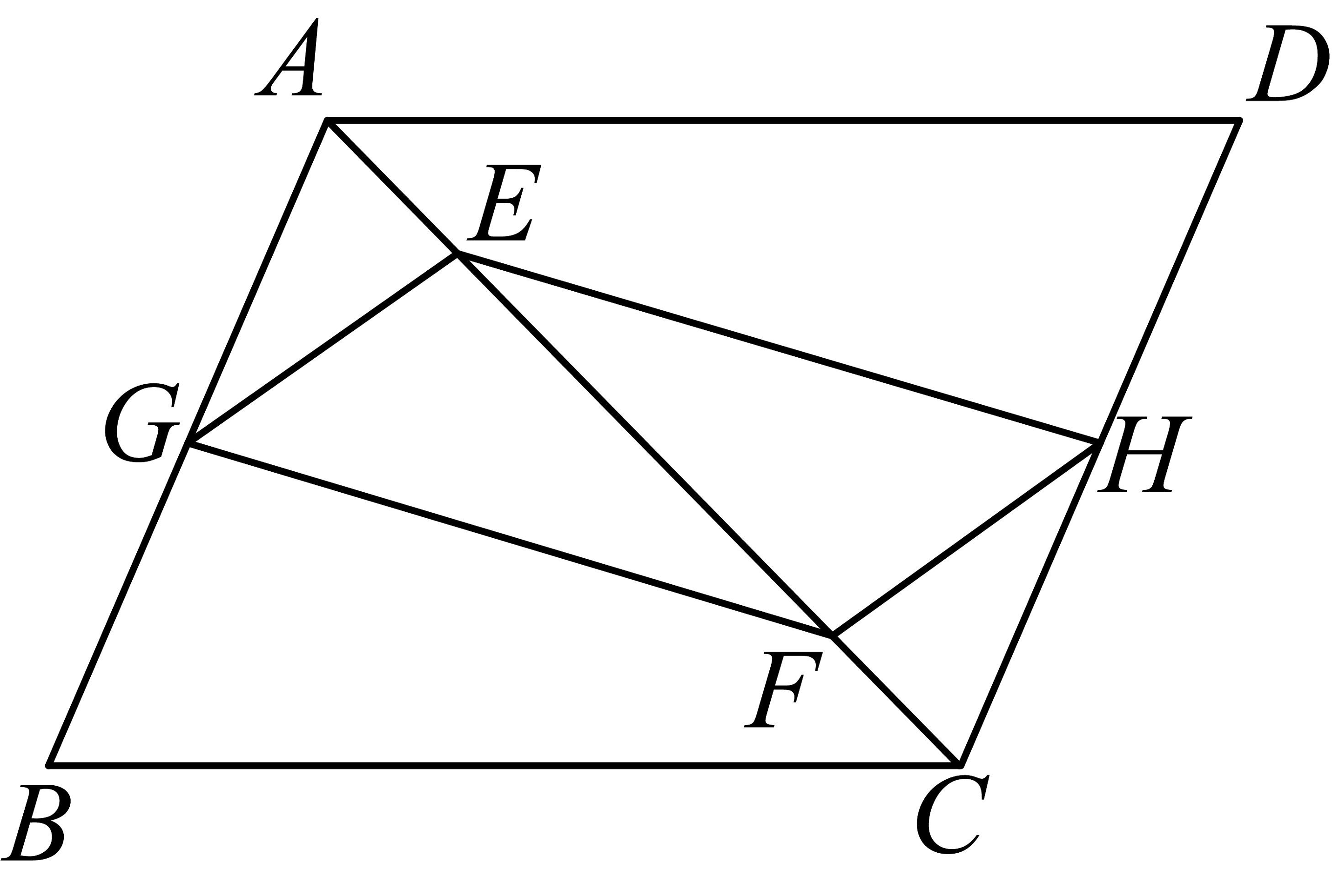 (1)、求证:四边形是平行四边形;(2)、连接交于点O,若 , , 求的长.
(1)、求证:四边形是平行四边形;(2)、连接交于点O,若 , , 求的长.三、拓展创新
-
20. 如图,在中, , , , , .
 (1)、求线段的长;(2)、如图2,连接 , 把线段绕点逆时针旋转90°到 , 连接 , 取线段的中点 , 连接 , 请判断线段与的数量关系,并说明理由;(3)、如图3,点是线段上一点,把线段绕点逆时针旋转45°得到 , 连接 , 请直接写出线段的最小值.
(1)、求线段的长;(2)、如图2,连接 , 把线段绕点逆时针旋转90°到 , 连接 , 取线段的中点 , 连接 , 请判断线段与的数量关系,并说明理由;(3)、如图3,点是线段上一点,把线段绕点逆时针旋转45°得到 , 连接 , 请直接写出线段的最小值.