湘教版数学八年级下册 1.2.1 平行四边形的性质 第二课时 同步分层练习
试卷更新日期:2026-01-21 类型:同步测试
一、夯实基础
-
1. 平行四边形具有的性质是( )A、四边相等 B、对角线相等 C、对角线互相平分 D、四个角都是直角2. 如图,在中,对角线与相交于点 , 则下列结论一定正确的是( )
 A、 B、 C、 D、3. 阅读材料:物理学中“力的合成”遵循平行四边形法则,即和的合力是以这两个力为邻边构成的平行四边形的对角线所表示的力 , 如图.
A、 B、 C、 D、3. 阅读材料:物理学中“力的合成”遵循平行四边形法则,即和的合力是以这两个力为邻边构成的平行四边形的对角线所表示的力 , 如图.
解决问题:设两个共点的合力为 , 现保持两力的夹角不变,使得其中一个力增大,则( )
A、合力一定增大 B、合力的大小可能不变 C、合力可能增大,也可能减小 D、合力一定减小4. 如图,在中,对角线 , 相交于点 , 下列结论正确的是( ) A、 B、 C、 与的周长相等 D、5. 如图,在平行四边形中, , , , 则的周长是( )
A、 B、 C、 与的周长相等 D、5. 如图,在平行四边形中, , , , 则的周长是( ) A、10 B、16 C、18 D、216. 如图,在中,对角线AC,BD相交于点O.若 , , , 则的长为( )
A、10 B、16 C、18 D、216. 如图,在中,对角线AC,BD相交于点O.若 , , , 则的长为( ) A、8 B、9 C、10 D、127. 如图,在中,对角线、相交于点 , 若 , , , 则度.
A、8 B、9 C、10 D、127. 如图,在中,对角线、相交于点 , 若 , , , 则度. 8. 如图,的对角线相交于点O, , , , 则的周长为cm.
8. 如图,的对角线相交于点O, , , , 则的周长为cm. 9. 如图,平行四边形中,对角线相交于点 , 过点的直线分别交于点 , 若平行四边形的面积为6,则图中阴影部分的面积是 .
9. 如图,平行四边形中,对角线相交于点 , 过点的直线分别交于点 , 若平行四边形的面积为6,则图中阴影部分的面积是 . 10. 如图平行四边形的对角线与交于点 O, . 求的周长.
10. 如图平行四边形的对角线与交于点 O, . 求的周长. 11. 如图,▱ABCD的对角线AC、BD相交于点O,AE=CF.求证:BE=DF.
11. 如图,▱ABCD的对角线AC、BD相交于点O,AE=CF.求证:BE=DF.
二、能力提升
-
12. 如图,平行四边形的对角线 , 相交于点 , 且 , , 则的周长为( )
 A、28 B、18 C、14 D、2413. 平行四边形的两条对角线分别为和 , 则其中一条边长的取值范围为( )A、 B、 C、 D、14. 如图,在中,、相交于点 , 若 , , 与的周长差为( ) .
A、28 B、18 C、14 D、2413. 平行四边形的两条对角线分别为和 , 则其中一条边长的取值范围为( )A、 B、 C、 D、14. 如图,在中,、相交于点 , 若 , , 与的周长差为( ) . A、4 B、3 C、2 D、115. 如图,平行四边形的对角线与相交于点O, , 若 , 则的长是( )
A、4 B、3 C、2 D、115. 如图,平行四边形的对角线与相交于点O, , 若 , 则的长是( ) A、 B、 C、 D、16. 有下列说法:
A、 B、 C、 D、16. 有下列说法:①平行四边形具有四边形的所有性质;
②平行四边形是轴对称图形;
③平行四边形的任意一条对角线可把平行四边形分成两个全等的三角形;
④平行四边形的两条对角线把平行四边形分成4个面积相等的小三角形.
其中正确说法的序号是( )
A、①②④ B、①②③ C、①③④ D、①②③④17. 如图,已知平行四边形的周长是12,对角线与交于点 , 的周长比的周长多1,则的长为. 18. 如图,在中, , 点E是中点,作于点F,已知 , , 则的长为 .
18. 如图,在中, , 点E是中点,作于点F,已知 , , 则的长为 . 19. 如图,▱ABCD的周长是 , 对角线相交于点O,且 , 则的周长为 .
19. 如图,▱ABCD的周长是 , 对角线相交于点O,且 , 则的周长为 . 20. 我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为和4,那么它的较长的对角线长为 .21. 如图,E、F是平行四边形的对角线上的两点, . 求证:四边形是平行四边形.
20. 我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为和4,那么它的较长的对角线长为 .21. 如图,E、F是平行四边形的对角线上的两点, . 求证:四边形是平行四边形. 22. 如图,在平行四边形中,对角线和交于点O,点E、F分别为的中点,连接 .
22. 如图,在平行四边形中,对角线和交于点O,点E、F分别为的中点,连接 .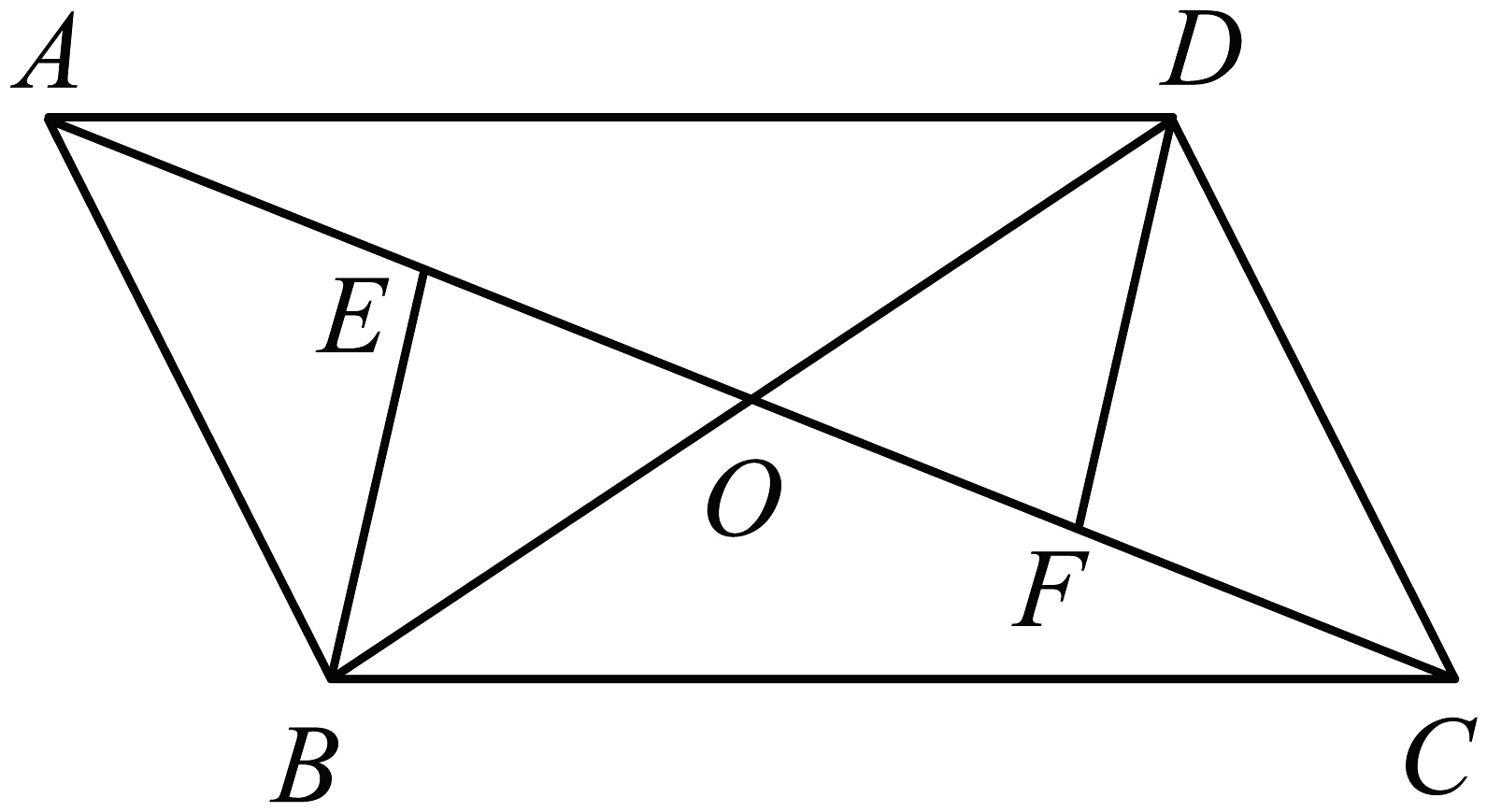 (1)、求证:;(2)、若 , 且 , 则的长为 .23. 如图,在中,对角线与相交于点 , 点分别为的中点,连结 .
(1)、求证:;(2)、若 , 且 , 则的长为 .23. 如图,在中,对角线与相交于点 , 点分别为的中点,连结 . (1)、求证: .(2)、若 , 求的周长.
(1)、求证: .(2)、若 , 求的周长.三、解答题
-
24. 一次数学探究活动,小强用两条直线把分割成四个部分,使含有一组对顶角的两个图形全等.(1)、在下面的三个平行四边形中分别画出满足小强分割方法的直线.
 (2)、从上述分割方法中,你发现所画的两条直线有什么规律吗?25. 【探索发现】小应发现:平行四边形两条对角线的平方和等于两邻边平方和的两倍.
(2)、从上述分割方法中,你发现所画的两条直线有什么规律吗?25. 【探索发现】小应发现:平行四边形两条对角线的平方和等于两邻边平方和的两倍.【推理论证】如图1,四边形是平行四边形,求证: .
小应的证明:作于点交的延长线于点 , 由四边形是平行四边形,容易证得(),得到 , . 设 , , .
在和中, .
在中, .
(1)请继续完成小应的证明;
【初步应用】(2)如图2,在平行四边形中,对角线 , 交于点 , , , , 求的长;
【拓展提升】(3)如图3,在中, , , 是斜边的三等分点, , , 求的长.
