浙教版数学八年级下册第2章一元二次方程提高检测卷

试卷更新日期：2026-01-12 类型：同步测试

进入出卷网下载

一、选择题(每题3分,共30分)

1. 下列方程中，属于一元二次方程的是（）

A、（3x-1）（x+2）=1 B、3x+2=0 C、3x+y=0 D、2x²- $\frac{1}{x}$ =0

查看试题解析
2. 用配方法解一元二次方程 $x^{2} - 8 x + 5 = 0$ 时，配方正确的是（）

A、 ${(x - 4)}^{2} = 5$ B、 ${(x - 4)}^{2} = 11$ C、 ${(x - 8)}^{2} = 63$ D、 ${(x - 8)}^{2} = 5$

查看试题解析
3. 若a-b+c=0，则关于x的一元二次方程 $a x^{2} - b x + c = 0 (a \neq 0)$ 必有一根是（）

A、0 B、1 C、-1 D、无法确定

查看试题解析
4. 已知关于 $x$ 的一元二次方程 $x^{2} + a x + 2 = 0$ 的一个根是 $x = - 2$ ，则 $a =$ （　　）

A、 $- 1$ B、1 C、2 D、 $3$

查看试题解析
5. 若关于x的一元二次方程mx²-4x+4=0有实数根，则m的值可能是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 为更好地开展劳动教育，学校决定在操场划出一块面积为480m²的长方形场地作为劳动基地若长方形场地的一边靠墙（墙足够长），另外三边由总长为70m的第笆围成，并且在平行于墙的边上设置两个开口宽为1m的进出门（如图），设靠墙的长方形边长为x（m），则下列方程正确的是（），

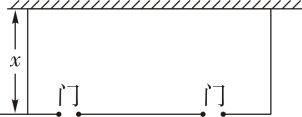A、x（72-2x）=480 B、x（68-2x）=480 C、x（72-x）=480 D、x（68-x）=480

查看试题解析
7. 在用求根公式 $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ 求一元二次方程的根时，小南正确地代入了a，b，c 得到 $x = \frac{3 \pm \sqrt{(- 3)^{2} - 4 \times 2 \times (- 1)}}{2 \times 2}$ ，则他求解的一元二次方程是（）

A、 $2 x^{2} - 3 x - 1 = 0$ B、 $2 x^{2} + 4 x - 1 = 0$ C、 $- x^{2} - 3 x + 2 = 0$ D、 $3 x^{2} - 2 x + 1 = 0$

查看试题解析
8. 近年来，中国旅游业呈现快速复苏与高质量发展态势．据统计，某旅游景点2022年游客量约为200万人次，2024年游客量达到450万人次．设该旅游景点游客量的年平均增长率为x ，则可列出方程（）

A、 $200 (1 + 2 x) = 450$ B、 $200 {(1 + x)}^{2} = 450$ C、 $200 {(1 + 2 x)}^{2} = 450$ D、 $200 {(1 - x)}^{2} = 450$

查看试题解析
9. 设 $x_{1} ， x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} - 7 x - 4 m^{2} = 0$ 的两个不同实数根，则 $x_{1} + x_{2}$ 的值是（）

A、 $- 4$ B、4 C、7 D、 $- 7$

查看试题解析
10. 已知a，b，c为常数，且满足 $(a - c)^{2} > a^{2} + c^{2}$ ，则关于x的方程 $a x^{2} + b x + c = 0$ 的根的情况是（）.

A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、有一根为0

查看试题解析

二、填空题(每题3分,共18分)

11. 若 $(a - 1) x^{2} - x + 1 = 0$ 是关于 x的一元二次方程，则a 的取值范围是.

查看试题解析
12. 已知 $a$ 是一元二次方程 $x^{2} + 2 x - 2 = 0$ 的一个实数根，求 $3 a^{2} + 6 a + 2025$ 的值为．

查看试题解析
13. 小马同学在解方程时，等号左边的一个数字不小心被墨水污染了，如右式：x²-＝0.已知一个根x₁=3，则另一个根x₂=.

查看试题解析
14. AI技术的应用越来越广泛，某AI应用软件2025年2月其点击率达到5.25亿次，2025年4月其点击率达到7.56亿次，设点击率从2月到4月的月平均增长率为x，则可列方程为.

查看试题解析
15. 定义新运算： $a * b = a^{2} + 4 a b + 1$ ，例如： $2 * 3 = 2^{2} + 4 \times 2 \times 3 + 1 = 29$ ．若方程 $x * 1 = m$ 有两个相等的实数根，则 $m$ 的值为．

查看试题解析
16. 若 $a$ 使得关于 $x$ 的分式方程 $\frac{a x - 1}{x - 2} - \frac{3}{2 - x} = 4$ 有整数解，且使得关于 $y$ 的一元二次方程 $(a - 2) y^{2} - 3 y + 1 = 0$ 有实数根，则所有满足条件的整数 $a$ 的和为．

查看试题解析

三、解答题(17-21,每题8分;22-23每题10分;24题12分,共72分)

17. 解下列方程：

(1)、 $x^{2} - 6 x = 1$

(2)、2x²－5x+2=0

查看试题解析
18. 关于x的一元二次方程 $(m - 1) x^{2} - 2 m x + m + 1 = 0$ （ $m \neq 1$ ）．

(1)、求证：方程总有两个不相等的实数根．

(2)、求证： $x = 1$ 是该方程的根．

查看试题解析
19. 2024年“广西三月三·八桂嘉年华”文化旅游品牌活动在南宁青秀山风景区拉开帷幕．大家身着民族服饰共赴一场民俗文化盛宴．如图，在地图上A、B两站直线距离为25km，C、D为青秀山和园博园民俗文化活动场地，且 $D A ⊥ A B$ 于A， $C B ⊥ A B$ 于B．已知 $D A = 15 km$ ， $C B = 10 km$ ，现在小明要在直线 $A B$ 上找到地点E，使得：

(1)、若要使得C、D两活动点到地点E的距离相等，则小明所在的E站应在离A站多少 $km$ 处？

(2)、若要使得地点E到C、D两地的距离之和最短，则小明所在的E站应在离A站多少 $km$ 处？并求出 $D E + C E$ 的最短距离．

查看试题解析
20. 某租赁公司拥有汽车100辆.据统计，当每辆车的月租金为3000元时，可全部租出.每辆车的月租金每增加50元，未租出的车将增加1辆.租出的车每辆每月的维护费为150元，未租出的车每辆每月只需维护费50元.

(1)、当每辆车的月租金定为3600元时，能租出多少辆？

(2)、当每辆车的月租金定为多少元时，租赁公司的月收益（租金收入扣除维护费）可达到306600元？

查看试题解析
21. 已知关于 $x$ 的方程 $x^{2} - 2 x + k - 1 = 0$ 有两个实数根．

(1)、求 $k$ 的取值范围；

(2)、若 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = x_{1}^{2} + 2 x_{2} - 1$ ，求 $k$ 的值．

查看试题解析
22. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根是另一个根的 $n$ 倍 $(n$ 为正整数），则称这样的方程为“ $n$ 倍根方程”．例如：方程 $x^{2} - 6 x + 8 = 0$ 的两个根分别是2和4，则这个方程就是“二倍根方程”；方程 $x^{2} - 4 x + 3 = 0$ 的两个根分别是1和3，则这个方程就是“三倍根方程”．

(1)、根据上述定义， $2 x^{2} - 5 x + 2 = 0$ 是“________倍根方程”；

(2)、若关于 $x$ 的方程 $x^{2} + 6 x + m = 0$ 是“三倍根方程”，求 $m$ 的值；

(3)、直线 $l_{1}$ ： $y = - x + 5$ 与 $x$ 轴交于点 $A$ ，直线 $l$ 过点 $B (- 1, 0)$ ，且与 $l_{1}$ 相交于点 $C (1, 4)$ ．若一个五倍根方程的两个根为 $x_{1}$ 和 $x_{2} (0 < x_{1} < x_{2})$ ，且点 $P (x_{1}, x_{2})$ 在 $△ A B C$ 的内部（不包含边界），求 $x_{1}$ 的取值范围．

查看试题解析
23. 对于任意两个非零实数a，b，定义运算“◎”如下：
$a ◎ b = {\begin{cases} \frac{a}{b} (a \geq b) \\ a b (a < b) \end{cases}$ 如： $4 ◎ 3 = \frac{4}{3}$ ， $2 ◎ 3 = 2 \times 3 = 6$ 。
根据上述定义，解决下列问题：

(1)、计算： $\sqrt{1000} ◎ \sqrt{10} =$ ， $\sqrt{2} ◎ (\sqrt{8} + 1) =$

(2)、若（x-1）◎（x+1）=2x+2，求x的值。

查看试题解析
24. 如图，在平面直角坐标系中，直线 $A B$ ： $y = - x + b$ 交 $x$ 轴正半轴于点 $A$ ，交 $y$ 轴正半轴于点 $B$ ，直线 $A B$ 过点 $P (1, 3)$

(1)、求直线 $A B$ 解析式；

(2)、连接 $O P$ ，将线段 $O P$ 沿 $x$ 轴正方向平移到 $D C$
①若 $S_{△ C D A} = \frac{1}{4} S_{△ A O B}$ ，求满足条件的点 $C$ 的坐标；
②在平移过程中，是否存在点 $C$ 使得 $△ A B C$ 为等腰三角形，若存在，请画出图形并求出点 $P$ 平移的距离，若不存在，请说明理由．

查看试题解析

浙教版数学八年级下册第2章 一元二次方程 提高检测卷

一、选择题(每题3分,共30分)

二、填空题(每题3分,共18分)

三、解答题(17-21,每题8分;22-23每题10分;24题12分,共72分)

浙教版数学八年级下册第2章一元二次方程提高检测卷