2025-2026学年北师大版数学七年级上册期末测试模拟题三

试卷更新日期：2026-01-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列运算正确的是（　　）

A、3x－2x＝1 B、2a＋3b＝5ab C、2ab＋ab＝3ab D、2（x＋1）＝2x＋1

查看试题解析
2. 下列运用等式性质进行的变形，不正确的是（）

A、如果 $3 + x = y + 3$ ，那么 $x = y$ B、如果 $x = y$ ，那么 $x - 3 = 3 - y$ C、如果 $\frac{x}{3} = \frac{y}{3}$ ，那么 $x = y$ D、如果 $3 x = 6 y$ ，那么 $x = 2 y$

查看试题解析
3. 某几何体从前面、左面、上面看到的图形如图所示，则该几何体为（　　）

A、
B、
C、
D、

查看试题解析
4. 在“ $5 \cdot 18$ 世界无烟日”来临之际，小明和他的同学为了解某街道大约有多少成年人吸烟，于是随机调查了该街道 $1000$ 个成年人，结果有 $180$ 个成年人吸烟．对于这个数据的收集与处理过程，下列说法正确的是（）

A、调查的方式是普查 B、该街道约有 $18 %$ 的成年人吸烟 C、该街道只有 $820$ 个成年人不吸烟 D、样本是 $180$ 个吸烟的成年人

查看试题解析
5. 如图，OB是 $∠ A O C$ 的平分线，OD是 $∠ C O E$ 的平分线．若 $∠ A O B = 40 °, ∠ D O E = 30 °$ ，则 $∠ B O D$ 是（）度．

A、40 B、60 C、70 D、80

查看试题解析
6. 对于任意四个有理数a，b，c，d，定义新运算： $|\begin{array}{l} a & b \\ c & d \end{array}| = a d - b c$ ．已知 $|\begin{array}{l} 2 x + 3 & 4 \\ 1 - x & 5 \end{array}| = 18$ ，则 $x$ 的值为（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $\frac{14}{19}$

查看试题解析
7. 某中学对学生最喜欢的课外体育项目进行了随机抽样调查，要求每人只能选择其中的一项，根据得到的数据，绘制的不完整统计图如图所示，则下列说法中不正确的是（）

A、这次调查的样本容量是200 B、全校1600名学生中，估计最喜欢排球的大约有240人 C、扇形统计图中，跳绳所对应的圆心角是45 D、被调查的学生中，最喜欢羽毛球的有60人

查看试题解析
8. 两根木条，一根长 $6 cm$ ，另一根长 $10 cm$ ，将它们一端重合且放在同一条直线上，此时两根木条的中点之间的距离为（）

A、 $2 cm$ B、 $8 cm$ C、 $2 cm$ 或 $5 cm$ D、 $2 cm$ 或 $8 cm$

查看试题解析
9. 我国古代著作《增删算法统宗》中记载了一首古算诗：＂庭前孩童闹如簇，不知人数不知梨．每人四梨多十二，每人六梨恰齐足．＂其大意是：＂孩童们在庭院玩要，不知有多少人和梨子．每人分4梨，多12梨；每人分6梨，恰好分完．＂设孩童有 $x$ 名，则可列方程为（）．

A、 $4 x + 12 = 6 x$ B、 $4 x - 12 = 6 x$ C、 $\frac{x}{4} - 12 = \frac{x}{6}$ D、 $\frac{x}{4} + \frac{x}{6} = 12$

查看试题解析
10. 将一张长方形纸片按如图所示的方式折叠， $E N ， E M$ 为折痕，折叠后点 $A^{'} ， B^{'}$ ， $E$ 在同一直线上，已知 $∠ A E N = 32 °$ ， $∠ E M B^{'}$ 的度数为（）

A、 $58 °$ B、 $32 °$ C、 $35 °$ D、 $45 °$

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，是一个正在绘制的扇形统计图，整个圆表示八年级全体同学参加拓展课的总人数，那么表示参加“生活数学”拓展课的人数占总人数的 $35 %$ 的扇形是．（填“ $N$ ”“ $M$ ”“ $P$ ”或“ $Q$ ”）

查看试题解析
12. 如图所示为哥哥与弟弟的聊天记录，则哥哥想买的平板电脑的原价为元．

查看试题解析
13. 方程 $(k + 1) x^{| k |} + 2 = 0$ 是一元一次方程，则 $k =$ .

查看试题解析
14. 如图，已知 $∠ A O B$ ， $O E$ 平分 $∠ A O C$ ， $O F$ 平分 $∠ B O C$ ．若 $∠ A O B + ∠ E O F = 156 °$ ，则 $∠ E O F$ 的度数是 °．

查看试题解析
15. 定义一种对正整数 $n$ 的“ $F$ ”运算：①当 $n$ 为奇数时， $F (n) = 3 n + 1$ ；②当 $n$ 为偶数时， $F (n) = \frac{n}{2^{k}}$ （其中 $k$ 是使 $F (n)$ 为奇数的正整数），两种运算交替重复进行，例如：取 $n = 24$ ，则，其中第1次 $F (24) = \frac{24}{2^{3}} = 3$ ，第2次 $F (3) = 3 \times 3 + 1 = 10$ ， $\dots$ ．若 $n = 5$ ，则第2025次“ $F$ ”运算的结果是．

查看试题解析
16. 如图，数轴上线段 $A B = 2$ ， $C D = 4$ ，点A在数轴上表示的数是 $- 10$ ，点C在数轴上表示的数是16，若线段 $A B$ 以6个单位长度/s的速度向右匀速运动，同时线段 $C D$ 以2个单位长度/s的速度向左匀速运动.当点B运动到线段 $C D$ 上时，P是线段 $A B$ 上一点，且有关系式 $\frac{B D - A P}{P C} = 3$ 成立，则线段 $P D$ 的长为.

查看试题解析

三、解答题（共8题，共72分）

17. 解方程：

(1)、 $2 (y + 2) - 3 (4 y - 1) = 9 (1 - y)$ ；

(2)、 $\frac{2 x + 1}{3} = 1 - \frac{x - 1}{5}$

查看试题解析
18. 先化简，再求值： $2 (a^{2} - 3 b^{2}) - \frac{1}{3} (9 a^{2} + 6 b^{2}) + 1$ ，其中 $a = - 1$ ， $b = - \frac{1}{2}$ ．

查看试题解析
19. $A Q I$ （空气质量指数）描述了空气清洁或者污染的程度，以及对健康的影响．环保局根据 $A Q I$ 将空气质量分为优、良、轻度污染、中度污染、重度污染、严重污染6个类别．小华根据环保局提供的数据绘制了某市2023年4月份和11月份每天的空气质量情况的相关统计图表（这两个月均为30天），请你根据以下信息回答问题：
4月份的空气质量情况
11月份的空气质量情况
空气质量类别
优
良
轻度污染
中度污染
重度污染
严重污染
天数
16
11
1
2
a
b
【整理与表示】

(1)、请你在图中补全4月份空气质量情况的条形统计图；

(2)、如果将4月份的空气质量情况制作成扇形统计图，则严重污染的天数所在扇形的圆心角度数为°；

(3)、由上表填空： $a + b =$ ．

(4)、【分析与判断】
请你结合上述信息，比较分析4月份和11月份的空气质量状况，并说明理由．

查看试题解析
20. 如图所示，点C在线段AB上，AC=8cm，CB=6cm，点M、N分别是AC、BC的中点．
（1）求线段MN的长．
（2）若C为线段AB上任意一点，满足AC+CB=acm，其他条件不变，你能猜想出MN的长度吗？并说明理由．
（3）若C在线段AB的延长线上，且满足AC﹣CB=bcm，M、N分别为AC、BC的中点，你能猜想出MN的长度吗？请画出图形，写出你的结论，并说明理由．

查看试题解析
21. 如图， $∠ A O C$ 和 $∠ B O D$ 共顶点， $∠ B O D$ 为直角， $O C$ 是 $∠ B O D$ 的角平分线， $∠ A O B = 150 °$ ．

(1)、求 $∠ A O C$ 的度数；

(2)、若 $∠ B O E : ∠ A O D = 2 : 3$ ，求 $∠ C O E$ 的度数．

查看试题解析
22. 某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的 $\frac{1}{2}$ 倍多25件，甲、乙两种商品的进价和售价如下表：
（注：获利=售价 $-$ 进价）
甲
乙
进价（元/件）
20
30
售价（元/件）
26
40

(1)、该超市购进甲、乙两种商品各多少件？

(2)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

(3)、该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多800元，求第二次乙商品是按原价打几折销售？

查看试题解析
23. 将连续的自然数1到150按图1的方式排列成一个方阵：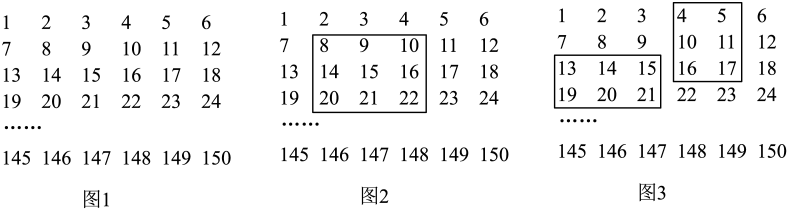

(1)、在图1中，第6行的第3个数是，第20行的最后一个数是；

(2)、如图2，用一个正方形在该方阵中任意框出9个数，请用代数方法说明这9个数之和一定是9的倍数；

(3)、如图3，若用如图所示的长方形在该方阵中任意框出6个数，这6个数之和能等于156吗？如果能，请求出这6个数；如果不能，请说明理由．

查看试题解析
24. 如图1， $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ， $∠ A O C = 30 °$ ，将一直角三角板（ $∠ M = 30 °$ ）的直角顶点放在点 $O$ 处，一边 $O N$ 在射线 $O A$ 上，另一边 $O M$ 与 $O C$ 都在直线 $A B$ 的上方．（注：本题旋转角度最多 $180 °$ ．）

(1)、将图1中的三角板绕点 $O$ 以每秒 $3 °$ 的速度沿顺时针方向旋转．如图2，经过 $t$ 秒后， $∠ A O N =$ 度（用含 $t$ 的式子表示），若 $O M$ 恰好平分 $∠ B O C$ ，则 $t =$ 秒（直接写结果）．

(2)、在（1）问的基础上，若三角板在转动的同时，射线 $O C$ 也绕 $O$ 点以每秒 $6 °$ 的速度沿顺时针方向旋转，如图3，经过 $t$ 秒后， $∠ A O C =$ ▲ 度（用含 $t$ 的式子表示）若 $O C$ 平分 $∠ M O N$ ，求 $t$ 为多少秒？

(3)、若（2）问的条件不变，那么经过秒 $O C$ 平分 $∠ B O M$ ？（直接写结果）

查看试题解析

空气质量类别	优	良	轻度污染	中度污染	重度污染	严重污染
天数	16	11	1	2	a	b

	甲	乙
进价（元/件）	20	30
售价（元/件）	26	40