2025-2026学年北师大版数学七年级上册期末测试模拟题二

试卷更新日期：2026-01-11 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列叙述不正确的是（）

A、两点之间，线段最短 B、 $a^{2} + 3 a + 5$ 是二次三项式 C、单项式 $- \frac{a b^{2} c^{3}}{3}$ 的次数是5 D、单项式 $- \frac{a b^{2} c^{3}}{3}$ 的系数是 $- \frac{1}{3}$

查看试题解析
2. 下列调查中，适宜采用全面调查方式的是（）

A、旅客上飞机前的安全检查 B、对广州市七年级学生身高现状的调查 C、对某品牌食品安全的调查 D、对一批灯管使用寿命的检查

查看试题解析
3. 下列时刻中，钟表的时针与分针所成的夹角是锐角的是（）．

A、11：15 B、9：00 C、6：00 D、3：30

查看试题解析
4. 一个由相同小立方块搭成的几何体，从正面、左面、上面看到的形状图如图所示，则搭成这个几何体的小立方块的个数为（）

A、4个 B、5个 C、6个 D、7个

查看试题解析
5. 如图，把一副三角板叠合在一起，则 $∠ A O B$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $30 °$ D、 $70 °$

查看试题解析
6. 线段 $A B = 5 cm$ ， $C$ 是直线 $A B$ 上的一点， $B C = 8 cm$ ，则 $A C$ 的长度必（）

A、 $13 cm$ B、 $3 cm$ C、 $3 cm$ 或 $13 cm$ D、以上都不对

查看试题解析
7. 在解方程 $\frac{x - 1}{2} - \frac{2 x + 3}{3} = 1$ 时，去分母正确的是（）

A、 $3 (x - 1) - 4 x + 3 = 1$ B、 $3 (x - 1) - 2 (2 x + 3) = 6$ C、 $3 x - 1 - 4 x + 3 = 1$ D、 $3 x - 1 - 4 x + 3 = 6$

查看试题解析
8. 如图是2025年1月份的日历图，用形如“H”字型框任意框出7个数，框出的7个数的和不可能是（）

A、60 B、91 C、105 D、119

查看试题解析
9. 如果一组数据a₁ ， a₂ ， …，a_n的平均数是2，那么一组新数据3a₁+2，3a₂+2，…，3a_n+2的平均数是（　　）

A、2 B、6 C、8 D、18

查看试题解析
10. 明代数学家程大位的《算法统宗》中有这样一个问题：“隔墙听得客分银，不知人数不知银，七两分之多四两，九两分之少半斤．”其大意为：有一群人分银子，如果每人分七两，则剩余四两，如果每人分九两，则还差半斤（注：明代时 $1$ 斤 $= 16$ 两，故有“半斤八两”这个成语）．设总共有 $x$ 个人，根据题意所列方程正确的是（）

A、 $7 x - 4 = 9 x + 8$ B、 $7 x + 4 = 9 x - 8$ C、 $\frac{x + 4}{7} = \frac{x - 8}{9}$ D、 $\frac{x - 4}{7} = \frac{x + 8}{9}$

查看试题解析

二、填空题（每题3分，共18分）

11. 第九届亚洲冬季运动会于 $2025$ 年 $2$ 月 $7$ 日在哈尔滨正式开幕，它点燃了中国人参与冰雪运动的热情，比赛项目包含“冰球”“单板滑雪”和其他项目共计 $64$ 个小项，根据调查各项目参赛人数结果绘制成扇形统计图（如图），则“单板滑雪”所在扇形的圆心角的度数为．

查看试题解析
12. 若方程 $(a - 2) x^{|a| - 1} = a + 3$ 是关于 $x$ 的一元一次方程，则 $a$ 的值是．

查看试题解析
13. 某种风衣每件按进价的1.8倍标价，再降价40元售出后，每件可以获得120元的利润，那么该种风衣每件的进价为元．

查看试题解析
14. 如图，AB=22cm，点C、D和E是线段AB上的点，且AC：CD：DE=1：2：3，若EB=4cm，则DB的长度是cm．

查看试题解析
15. 若关于x的方程 $x - \frac{2 - m x}{6} = \frac{x + 1}{3}$ 的解是整数解，m是整数，则所有m的值加起来为．

查看试题解析
16. 如图，一副三角板（直角顶点重合）摆放在桌面上，若 $∠ A O D = 160 °$ ，则 $∠ B O C =$ ．

查看试题解析

三、解答题（共8题，共72分）

17. 解方程：

(1)、 $4 x - 3 (20 - x) = 3$ ；

(2)、 $\frac{2}{3} x - 7 = \frac{9 x - 2}{6}$ ．

查看试题解析
18. 先化简，再求值： $(2 x^{2} - 5 x y + 2 y^{2}) - 2 (x^{2} - 3 x y + 2 y^{2})$ ，其中 $x = \frac{1}{2}, y = - 2$ ．

查看试题解析
19. 2025年3月22日是第三十二届“世界水日”，世界水日提醒我们：水是生命之源，需全世界共同行动保护这一珍贵资源．某市在实施居民用水定额管理前，对居民生活用水情况进行调查，通过调查获得了一些家庭去年的月均用水量（单位：吨）．以下是整理数据后的不完整统计表和统计图．
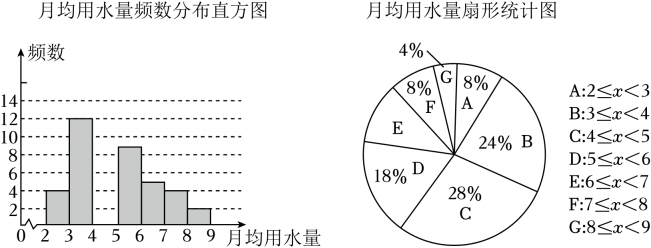
月均用水量频数分布表
分组
频数
2≤x＜3
4
3≤x＜4
12
4≤x＜5
a
5≤x＜6
9
6≤x＜7
5
7≤x＜8
4
8≤x＜9
2
请根据不完整的图表中提供的信息解答下列问题：

(1)、填空：
①本次调查的样本容量是  ；
②频数分布表中a的值为  ；
③月均用水量扇形统计图中，分组“E”的扇形圆心角度数是  ；

(2)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费．若要使60%的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？请说明理由．

查看试题解析
20. 如图，点C是线段AB上一点，点M是线段AC的中点，点N是线段BC的中点．

(1)、如果AB=20cm，AM=6cm，求NC的长；

(2)、如果MN=6cm，求AB的长．

查看试题解析
21. 如图，已知O为直线 $A B$ 上一点， $∠ A O D = α$ ， $∠ C O D = 90 °$ ．

(1)、若 $α = 55 °$ ，求 $∠ B O C$ 的度数；

(2)、若 $O F$ 平分 $∠ B O C$ ，求 $∠ A O F$ （用含 $α$ 的式子表示）．

查看试题解析
22. 为了丰富学生的课余生活、拓展学生的视野，学校小卖部准备购进甲、乙两类中学生书刊．其中甲、乙两类书刊的进价和售价如表：
甲
乙
进价（元/本）
10
8
售价（元/本）
20
13

(1)、第一次小卖部购进的甲、乙两类书刊共500本，全部售完后总利润（利润＝售价－进价）为4250元，求小卖部甲、乙两类书刊分别购进多少本？

(2)、第二次小卖部购进了与上次一样多的甲、乙两类书刊，由于两类书刊进价都比上次优惠了10%，小卖部准备对甲书刊进行降价出售，乙书刊价格不变，全部售完后总利润比上次还少赚了230元，求甲书降价了几元？

查看试题解析
23. 【问题初探】
（1）数学活动课上，李老师让同学们准备一副三角尺，并利用它们作出一些角，例如 $30 ° ， 45 ° ， 60 ° ， 90 °$ ．
①小明利用三角尺作出了一个 $120 °$ 的角；
②小乐利用三角尺作出了一个 $15 °$ 的角；
除上述提到的这些度数之外，你还能用三角尺作出度的角（写出一种即可）．
【提出问题】
（2）如图1所示，李老师将两个三角尺放置在一起，于是产生了新的数学问题， $∠ A O B = ∠ D C O = 90 °$ ， $∠ A = 45 °$ ， $∠ D O C = 30 °$ ，在 $∠ B O D$ ， $∠ A O C$ （ $0 ° < ∠ B O D \leq 180 °$ ， $0 ° < ∠ A O C \leq 180 °$ ）内作射线 $O P$ ， $O Q$ ，且 $∠ P O B = 3 ∠ D O P$ ， $∠ Q O A = 3 ∠ Q O C$ ，则 $∠ P O Q =$ 度；
【学以致用】
（3）如图2，小亮忘记了带三角尺，用纸片制作了任意两个三角形，其中 $∠ A O B = α$ ， $∠ C O D = β$ ，他把这两个三角形的顶点 $O$ 及边 $O D$ ， $O B$ 重合在一起，三角形 $A O B$ 固定，将三角形 $C O D$ 绕点 $O$ 顺时针旋转，当边 $O C$ 与 $O A$ 重合时，停止运动．在此过程中，在 $∠ B O D$ ， $∠ A O C$ 内作射线 $O P$ ， $O Q$ ，使 $∠ B O D = 3 ∠ P O D$ ， $∠ A O C = 3 ∠ Q O C$ ．这时，小明说“ $∠ P O Q$ 的度数是一个定值，并且可以用 $α$ ， $β$ 表示出来”；小乐说“ $∠ P O Q$ 的度数是一个随机值，无法用 $α$ ， $β$ 表示出来”，请你帮小亮判定一下谁的说法正确，并说明理由．

查看试题解析

分组	频数
2≤x＜3	4
3≤x＜4	12
4≤x＜5	a
5≤x＜6	9
6≤x＜7	5
7≤x＜8	4
8≤x＜9	2

	甲	乙
进价（元/本）	10	8
售价（元/本）	20	13