浙教版数学八年级下册第2章一元二次方程培优检测卷

试卷更新日期：2026-01-11 类型：单元试卷

进入出卷网下载

一、选择题(每题3分,共30分)

1. 下列方程中，一定是关于x的一元二次方程是（）

A、 $2 a x + x + 1 = 0$ B、 $\frac{1}{x} + x = 0$ C、 $x y + x = 0$ D、 $x^{2} + x = 0$

查看试题解析
2. 方程 $3 x^{2} = 5 x + 7$ 的二次项系数、一次项系数，常数项分别为（）

A、3，5，7 B、3， $- 5$ ， $- 7$ C、3， $- 5$ ， 7 D、3，5， $- 7$

查看试题解析
3. 用配方法解方程x²+4x-10=0时，下列配方结果正确的是（）

A、（x-2）²=12 B、（x+2）²=12 C、（x-2）²=14 D、（x+2）²=14

查看试题解析
4. 方程（x－2）²=4（x-2）（）

A、4 B、－2 C、4或－6 D、6或2

查看试题解析
5. 关于一元二次方程 $2 x^{2} + 5 x + 8 = 0$ 的根的情况，下列说法正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定是否有实数根

查看试题解析
6. 《九章算术》是我国传统数学中重要的著作之一，奠定了我国传统数学的基本框架，其中方程术是《九章算术》最高的数学成就.《九章算术》记载：“今有户高多于广六尺八寸，两隅相去适一丈.问户高、广各几何？”大意：有一扇形状是长方形的门，它的高比宽多6尺8寸，它的对角线长1丈，问它的高与宽各是多少（1丈 $= 10$ 尺，1尺 $= 10$ 寸）？设长方形门宽为x尺，则所列方程为（）.

A、 $x^{2} + {(x + 6.8)}^{2} = 10^{2}$ B、 $x^{2} + {(x - 6.8)}^{2} = 10^{2}$ C、 ${(x + 6.8)}^{2} - x^{2} = 10^{2}$ D、 $x^{2} + {6.8}^{2} = 10^{2}$

查看试题解析
7. 若关于 $x$ 的一元二次方程 $(k - 1) x^{2} - 2 k x + k - 3 = 0$ 有实数根，则 $k$ 的取值范围为（）

A、 $k \geq \frac{3}{4}$ B、 $k \geq \frac{3}{4}$ 且 $k \neq 1$ C、 $k \geq 0$ D、 $k \geq 0$ 且 $k \neq 1$

查看试题解析
8. 关于x的一元二次方程 $a x^{2} + b x + c = 0 (a c \neq 0)$ 一个实数根为 $x = 2024$ ，则方程 $c x^{2} + b x + a = 0$ 一定有实数根x=（）

A、2024 B、 $\frac{1}{2024}$ C、-2024 D、 $- \frac{1}{2024}$

查看试题解析
9. 设x₁ ， x₂是关于x的一元二次方程x²-7x-4m²=0的两个不同实数根，则x₁+x₂的值是（）

A、-4 B、4 C、7 D、-7

查看试题解析
10. 关于x的一元二次方程 $a x^{2} - a x + c = 0 (a \neq 0)$ 没有实数根，则系数a， c 可能满足（）

A、 $a < 0$ ， $a - 4 c < 0$ B、 $a < 0$ ， $a + 4 c < 0$ C、 $a > 0$ ， $a + 4 c < 0$ D、 $a > 0$ ， $a - 4 c < 0$

查看试题解析

二、填空题(每题3分,共18分)

11. 关于x的一元二次方程x²+5x-2p=0的一个根为2，则p的值是.

查看试题解析
12. 已知一元二次方程 $x^{2} - k x + 3 = 0$ 有一个根为1，则另一个根为．

查看试题解析
13. 已知 $α, β$ 是一元二次方程 $x^{2} - 2024 x - 2025 = 0$ 的两个根，则 $α^{2} - 2025 α - β$ 的值等于．

查看试题解析
14. 已知两个连续正奇数的积是143，设其中较小的正奇数是x，可列方程.

查看试题解析
15. 若t是方程 $- 2 x^{2} + x + 9 = 0$ 的一个根，则 $(t - 1) (2 t + 1)$ 的值为．

查看试题解析
16. 如图，正方形 ABCD 的边长为 13，以 BC 为斜边向内作 $Rt△ B C F$ ， $∠ F = 9 0^{°}$ ， $B F > C F$ ， $A E ⊥ B F$ 于点 E，连结 DE.若 $E F = 7$ ，则 $△ A E D$ 的面积为.

查看试题解析

三、解答题(17-21每题8分,22-23每题10分,24题12分,共72分)

17. 解方程：

(1)、 $x (x - 4) + 5 (x - 4) = 0$ ；

(2)、 $x^{2} + 4 x - 1 = 0$ ．

查看试题解析
18. 甲、乙两位同学解方程 $2 (x - 2) = (x - 2)^{2}$ 的过程如下框：
甲： $2 (x - 2) = (x - 2)^{2}$
两边同除以 $(x - 2)$ 得：
$2 = x - 2$
则 $x = 4$
（）
乙：
移项得 $2 (x - 2) - (x - 2)^{2} = 0$
提公因式 $(x - 2) (2 - x - 2) = 0$
则 $x - 2 = 0$ 或 $2 - x - 2 = 0$
$∴ x_{1} = 2, x_{2} = 0$
（）
你认为他们的解法是否正确？若正确请在括号内打“√”，若错误打“×”，并写出你的解答过程．

查看试题解析
19. 已知关于 $x$ 的一元二次方程 $x^{2} - 6 x - m = 0$ ．

(1)、若方程有两个实数根，求 $m$ 的取值范围；

(2)、在（1）中，设 $x_{1}, x_{2}$ 是该方程的两个根，且 $x_{1} + x_{2} - 2 x_{1} x_{2} = 0$ ，求 $m$ 的值．

查看试题解析
20. 五一假期，某著名景区在5月1日至3日期间的游客人数逐日增加，5月4日至5日游客人数大幅减少.据统计，5月1日的游客人数为1.5万人，5月3月的游客人数为2.16万人.

(1)、求5月1日至3日到该景区的游客人数的日平均增长率；

(2)、5月4日至5日这两天到该景区的游客总人数不会超过5月1日至3日游客总人数的 $\frac{1}{3}$ ，求5月4日至5日到该景区的游客人数平均每天最多是多少万人？

查看试题解析
21. 已知一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ．

(1)、若方程的一个根为2，求 $\frac{2 b + c}{a}$ 的值．

(2)、当 $b - a c = 1$ 时，求证：方程有两个实数根．

查看试题解析
22. 已知关于x的方程 $x^{2} - (2 k + 1) x + 4 (k - \frac{1}{2}) = 0$ ．

(1)、求证：无论k取何值，此方程总有实数根；

(2)、若等腰△ABC的一边长a＝4，另两边b、c恰好是这个方程的两个根，求这个等腰三角形的周长是多少？

查看试题解析
23. 用一张长为40cm，宽为25cm的长方形硬纸片，裁去一部分后折成纸盒。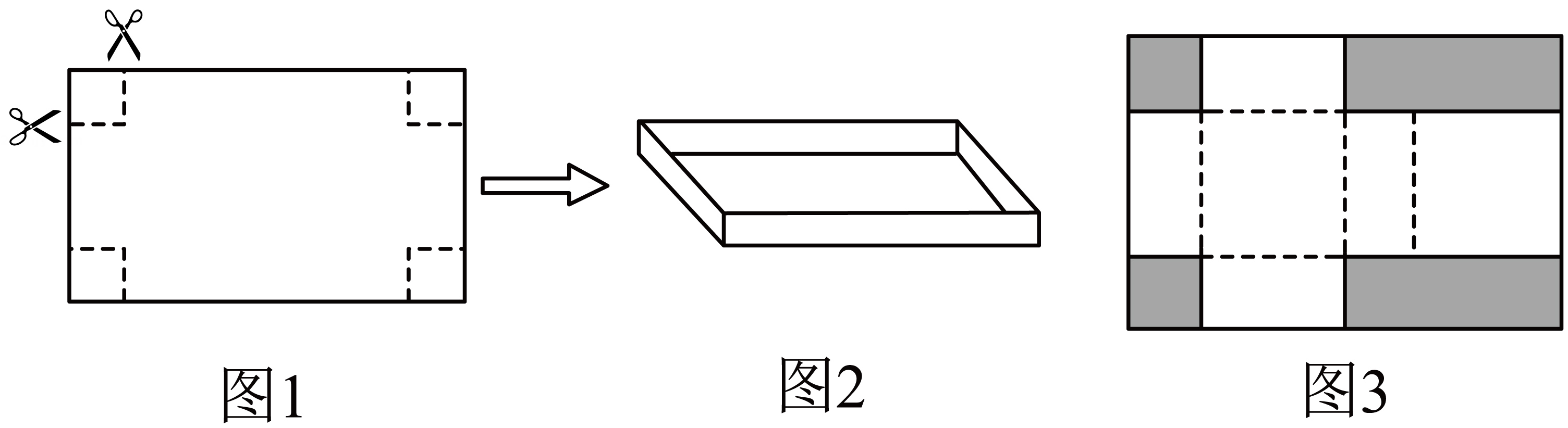

(1)、如图1裁去角上四个小正方形之后，折成如图2的无盖纸盒。若纸盒底面积为450cm² ，则纸盒的高是多少？

(2)、如图3，在纸片左边的两个角裁去两个正方形，纸片右边的两个角裁去两个长方形之后，将剩下的纸片（空白部分）折成一个有盖的纸盒。若折成纸盒的表面积为912cm² ，则裁去的正方形的边长是多少？

查看试题解析
24. 定义：两根都为整数的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 称为“全整根方程，代数式 $\frac{4 a c - b^{2}}{4 a}$ 的值为该“全整根方程”的“最值码”，用 $Q (a, b, c)$ 表示，即 $Q (a, b, c) = \frac{4 a c - b^{2}}{4 a}$ ，若另一关于 $x$ 的一元二次方程 $p x^{2} + q x + r = 0 (p \neq 0)$ 也为“全整根方程”，其“最值码”记为 $Q (p, q, r)$ ，当满足 $Q (a, b, c) - Q (p, q, r) = c$ 时，则称一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 是一元二次方程 $p x^{2} + q x + r = 0 (p \neq 0)$ 的“全整根伴侣方程”．

(1)、“全整根方程” $x^{2} - 3 x + 2 = 0$ 的“最值码”是______．

(2)、若（1）中的方程是关于 $x$ 的一元二次方程 $x^{2} + q x - 2 = 0$ 的“全整根伴侣方程”，求 $q$ 的值．

(3)、若关于 $x$ 的一元二次方程 $x^{2} + (1 - m) x + m - 2 = 0$ 是 $x^{2} + (n - 1) x - n = 0$ （ $m, n$ 均为正整数）的“全整根伴侣方程”，求 $m - n$ 的值．

查看试题解析

浙教版数学八年级下册第2章 一元二次方程 培优检测卷

一、选择题(每题3分,共30分)

二、填空题(每题3分,共18分)

三、解答题(17-21每题8分,22-23每题10分,24题12分,共72分)

浙教版数学八年级下册第2章一元二次方程培优检测卷