第17章《一元二次方程》提升卷—沪科版数学八（下）分层单元测

试卷更新日期：2026-01-11 类型：单元试卷

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 下列说法中，正确的是（）

A、形如 $a x^{2} + b x + c = 0$ 的方程叫做一元二次方程 B、方程 $2 x^{2} + 3 x = 6$ 不含常数项 C、一元二次方程中，一次项系数、常数项不能为0 D、 ${(2 - x)}^{2} = 0$ 是一元二次方程

查看试题解析
2. 某超市一月份的营业额为250万元，二月份、三月份每月的营业额逐月递增，到三月底，这三个月总营业额为 910万元.设营业额的月平均增长率为x，由题意可列方程为 ( )

A、 $250 {(1 + x)}^{2} = 910$ B、250+250(1+2x)=910 C、250(1+2x)=910 D、250+250(1+x)+250(1+x)²=910

查看试题解析
3. 关于x的一元二次方程 $a x^{2} + b x + c = 0 (a c \neq 0)$ 一个实数根为 $x = 2024$ ，则方程 $c x^{2} + b x + a = 0$ 一定有实数根x=（）

A、2024 B、 $\frac{1}{2024}$ C、-2024 D、 $- \frac{1}{2024}$

查看试题解析
4. 已知x₁ ， x₂是关于x的方程 $x^{2} - 2 (m + 1) x + m^{2} + 5 = 0$ 的两个实数根，已知等腰△ABC的一边长为3，若x₁ ， x₂恰好是△ABC另外两边长，则△ABC周长为( )

A、9 B、9或11 C、13 D、9或13

查看试题解析
5. 若关于x的一元二次方程 $a x^{2} + b x +$ 5=0有一个根为2025，则方程 $a {(x + 1)}^{2} + b （ x +$ 1）=-5必有一个根为（）

A、2024 B、2023 C、2022 D、2021

查看试题解析
6. 已知关于x的两条一元二次方程①ax²+bx+c=0②cx²+bx+a=0（a≠c≠0）.甲、乙两同学分别提出了以下两种不同的观点：
甲同学，若方程①有一个解为x=m（m≠0），则方程②一定有一个解为×= $\frac{1}{m}$
乙同学：若方程①②有公共解，则公共解为x₁=1，x₂=-1
正确的结论为（）

A、甲同学的观点正确，乙同学的观点错误 B、甲同学的观点错误，乙同学的观点正确 C、甲、乙同学的观点均正确 D、甲、乙同学的观点均错误

查看试题解析
7. 已知关于 $x$ 的方程 $a (x - 1) (x - m) = 0$ 与 $a (x - n)^{2} = b$ 有相同的解，则 $m$ 与 $n$ 之间的等量关系为（）

A、 $m + n = 1$ B、 $m - n = 1$ C、 $m + 2 n = - 1$ D、 $m - 2 n = - 1$

查看试题解析
8. 王老师设计了接力游戏：每人只能看到前一人的方程，并继续进行变形，将结果传递给下一人，最终求出方程的解，过程如图所示。
上述求解过程中，错误的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 对于关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的根的情况，有以下四种表述：
①当 $a < 0 ， b + c > 0 ， a + c < 0$ 时，方程一定没有实数根
②当 $a < 0 ， b + c > 0 ， b - c < 0$ 时，方程一定有实数根
③当 $a > 0 ， a + b + c < 0$ 时，方程一定没有实数根
④当 $a > 0 ， b + 4 a = 0 ， 4 a + 2 b + c = 0$ 时，方程一定有两个不相等的实数根；其中表述正确的序号是（）

A、① B、② C、③ D、④

查看试题解析
10. 我国古代数学家赵爽（公元3~4世纪）在其所著的《勾股圆方图注》中记载过一元二次方程（正根）的几何解法．以方程 $x^{2} + 5 x - 14 = 0$ 即 $x (x + 5) = 14$ 为例说明，记载的方法是：构造如图面积是 ${(x + x + 5)}^{2}$ 的大正方形．同时它又等于四个矩形的面积加上中间小正方形的面积，即 $4 \times 14 + 5^{2} = 81$ ，因此 $x = 2$ ．则在下列四个构图中，能正确说明方程 $x^{2} - 3 x - 10 = 0$ 解法的构图是（）

A、 B、 C、 D、

查看试题解析
11. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列说法：
①若 $a - b + c = 0$ ，则 $b^{2} - 4 a c \geq 0$ ；
②若方程 $a x^{2} + c = 0$ 有两个不相等的实根，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $x_{0}$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a x_{0} + b)}^{2}$
其中正确的：（）

A、只有① B、只有①② C、①②③ D、只有①②④

查看试题解析
12. 如图，Rt△ACB中，∠C＝90°，AC＝7，BC＝5，点P从点B出发向终点C以1个单位长度/s移动，点Q从点C出发向终点A以2个单位长度/s移动，P、Q两点同时出发，一点先到达终点时P、Q两点同时停止，则（）秒后，△PCQ的面积等于4．

A、1 B、2 C、4 D、1或4

查看试题解析

二、填空题：本大题共4小题，每小题4分，共16分.只要求填出最后结果.

13. 若关于x的一元二次方程kx²-5x+5=0有两个不相等的实数根，则k的值可以为（写出一个即可）.

查看试题解析
14. 今年秋冬季是支原体肺炎的感染高发期，戴口罩可以有效遏制支原体肺炎病毒的传染．现在有一个人患了支原体肺炎，经过两轮传染后共有49人患了支原体肺炎（假设每个人每轮传染的人数同样多），设每轮传染中平均一个人传染了x个人，则可列方程为．

查看试题解析
15. 刘聪同学发明了一个魔术盒，当任意实数对(a，b)进入其中时，会得到一个新的实数 $a^{2} + b - 1$ .例如，把(3，-2)放入其中，就会得到 $3^{2} + (- 2) - 1 = 6$ .现将实数对(m，-2m)放入其中，得到实数-1，则m的值是.

查看试题解析
16. 如果关于x的一元二次方程a²+bx+c=0有两个实数根，且其中一个根为另外一个根的2倍，则称这样的方程为“倍根方程”，以下关于倍根方程的说法，正确的有（填序号）
①方程x²-x-2=0是倍根方程；
②若（x-2)（mx+n)=0是倍根方程：则4m²+5mn+n²=0；
③若p，q满足pq=2，则关于x的方程叔px²+3x+q=0是倍根方程；
④若关于x的一元二次方程ax²+bx+c=0是倍根方程，则必有2b²=9ac·

查看试题解析

三、解答题：本大题共7小题，共68分.

17. 解下列方程：

(1)、 $x (x + 5) = 24$ ；

(2)、 $2 {(x - 1)}^{2} - 8 = 0$ ；

(3)、 $(y + 3) (1 - 3 y) = 1 + 2 y^{2}$ ；

(4)、 ${(1997 - x)}^{2} + {(x - 1996)}^{2} = 1$ ．

查看试题解析
18. 下面是李华用因式分解法解一元二次方程的过程，请仔细阅读，并完成相应的问题．
解一元二次方程： $3 x (3 x - 1) = 1 - 3 x$ ：
解：原方程可以化简为 $3 x (3 x - 1) = - (3 x - 1) . \dots \dots$ 第一步
两边同时除以 $(3 x - 1)$ 得 $3 x = - 1 . \dots \dots$ 第二步
系数化为 $1$ ，得 $x = \frac{1}{3} . \dots \dots$ 第三步
任务：

(1)、李华的解法是不正确的，他从第步开始出现了错误．

(2)、请完成这个方程的正确解题过程．

查看试题解析

19. 阅读与思考

观察下列方程系数的特征及其根的特征，解决问题：

方程及其根		方程及其根
方程及其关联方程	方程的根	方程及其关联方程	方程的根
$① 2 x^{2} - 3 x + 1 = 0$	$x_{1} = \frac{1}{2}$ ， $x_{2} = 1$	$① x^{2} + 2 x - 3 = 0$	$x_{1} = - 3$ ， $x_{2} = 1$
$② 2 x^{2} + 3 x + 1 = 0$	$x_{1} = - \frac{1}{2}$ ， $x_{2} = - 1$	$② x^{2} - 2 x - 3 = 0$	$x_{1} = 3$ ， $x_{2} = - 1$
$⋯ ⋯$		$⋯ ⋯$

(1)、请描述一元二次方程和关联方程的系数特征及它们根的关系特征．

(2)、方程

x^{2} - 2 x - 4 = 0

和

x^{2} + 2 x - 4 = 0

是不是关联方程？求解两个方程并判断两个方程的根是否符合根的关系特征．

(3)、请以一元二次方程

a x^{2} + b x + c = 0

（

a \neq 0

，

b^{2} - 4 a c \geq 0

）为例证明关联方程根的关系特征．

查看试题解析

20. 春节期间，九（1）班全体同学通过视频电话的方式互相拜年，如果该班共有 45名同学，若每两名同学之间仅通过一次视频电话，那么全班同学共通过多少次视频电话呢？我们可以用下面的方式来解决问题。用点 A1 ， A2 ， A3 ，…， A45 分别表示第1名同学，第2名同学，第3名同学……第45名同学，
把通话次数 y 与该班级人数 x 之间的关系用以下图表表示：

(1)、填写图中第四个图中 y 的值为，第五个图中 y 的值为。
通过探索发现，通话次数 y 与该班级人数 x 之间的关系式为。

(2)、若九（1）班全体女生相互之间共通话300次，该班共有多少名女生？

查看试题解析
21. 世界杯是世界上级别最高的足球赛事，2022年世界杯在卡塔尔隆重举行，今年世界杯的吉祥物是“拉伊卜”，它的设计灵感来源于阿拉伯标志型的白头巾，某网店现售有一大一小两种型号的“拉伊卜”摆件，已知每个大摆件的售价是每个小摆件售价的2倍还多60元，420元可购买一个大摆件和一个小摆件．

(1)、每个“拉伊卜”大摆件和小摆件的售价分别是多少？

(2)、第一天该网店按照原售价卖出大摆件30个，小摆件100个，因为小摆件库存量大，第二天商家调整了销售方案，大摆件的价格不变，小摆件的价格下调 $2 m$ 元，调整后，当天大摆件的销量下降了 $\frac{1}{2} m$ 个，小摆件的销量增加了 $\frac{5}{2} m$ 个，当天的销售额达到了20520元，求降价后的小摆件的价格．

查看试题解析

22. 根据以下素材，探索完成任务

如何利用闲置纸板箱制作储物盒
素材1	如图1是小慧家的一个储物位置，该储物位置的底面尺寸如图2所示
素材2	如图3，4是利用闲置纸板箱拆解出①，②两种宽均为 $a$ （ $c m$ ）（ $a < 50$ ）的长方形纸板．

素材3	小慧分别将长方形纸板①和②以不同的方式制作储物盒．
	将纸板①裁去角上4个长宽之比为 $1 : 2$ 的小长方形，折成一个无盖有把手的长方形储物盒（如图5）．	将纸板②裁出两个正方形，再裁出阴影部分放在上面的位置，制作一个无盖纸盒
目标1	（1）若按照长方形纸板①的制作方式制成的储物盒恰好完全盖住储物区底面，则长方形纸板的宽 $a$ 为 ▲ $c m$ （ $a < 50$ ）
利用目标1计算所得的数据 $a$ ，进行进一步探究．
目标2	（2）按照长方形纸板①的制作方式，求当储物盒的底面积是 $832 c m^{2}$ 时储物盒的体积为多少？
目标3	（3）按照长方形纸板②的制作方式制作储物盒，则储物盒的底面积为多少？

查看试题解析

23. “数形结合”是数学中的一种基本思想方法.我国著名数学家华罗庚对此曾有生动的描述：“数以形而直观，形以数而入微”.下面我们分别以我国三国时期的数学家赵爽（公元3～4世纪）和公元9世纪的阿拉伯数学家阿尔•花拉子在解一元二次方程x²+2x-35=0即x（x+2）=35时的做法为例加以说明.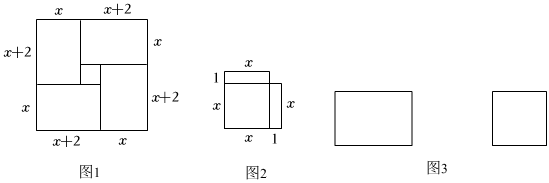
【学习研究】数学家赵爽的做法是，用四个边长分别为x ， x+2且面积为x（x+2）=35的矩形构造成图1形状的大正方形，然后用两种方式表示出大正方形的面积，得到（x+2+x）²=4×35+2² ，从而得到一个正数解x=5.阿拉伯数学家阿尔•花拉子米采用的方法是用一个边长为x的正方形和2个边长分别为x ， 1的矩形构造出图2的形状（面积为x²+2x=35）并把它补成一个大正方形，然后也是用两种方式表示出大正方形的面积，得到（x+1）²=（x²+2x）+1²=35+1，从而得到一个正数解x=5.

(1)、图1中，小正方形的边长为 ▲ ，将图2中补充完整（补充的部分用阴影表示）；

(2)、【类比迁移】小明想通过以上述构造图形的方法来解一元二次方程方程x²+6x-55=0.
①请分别构造以上两种图形，并在图中标注出相关线段的长；（注：第一种方法中已经画好了一个矩形，第二种方法中已经画好了一个正方形，请在已经画好的图形上进行补充）
②请分别根据所画图形，求出方程x²+6x-55=0的一个正数解.
（注：需要写出必要的推算过程）

(3)、【拓展应用】一般地，形如x²+ax=b的一元二次方程可以构造类似以上图形来求解，请选择其中的一种方法，进行图形构造，且在图中标注出相关线段的长，并直接写出该方程的正数解与负数解.

查看试题解析