第17章《一元二次方程》基础卷—沪科版数学八（下）分层单元测

试卷更新日期：2026-01-11 类型：单元试卷

进入出卷网下载

一、选择题：本大题共12小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 下列方程是一元二次方程的是 ( )

A、 $x + y^{2} = 2$ B、x+4=2 C、 $x^{2} + 4 x = 2$ D、 $x^{2} + \frac{1}{x} = 2$

查看试题解析
2. 把一元二次方程(2一x)(x+3)=1化成一般形式，正确的是 ( )

A、 $x^{2} + x - 5 = 0$ B、 $x^{2} - 5 x - 5 = 0$ C、 $x^{2} - 5 x - 6 = 0$ D、 $- x^{2} - x + 6 = 0$

查看试题解析
3. 关于x的一元二次方程 $(a - 1) x^{2} - 2 a x + a^{2} - 1 = 0$ 的一个根为0，则a的值为（）

A、2 B、 $- 1$ C、1或 $- 1$ D、2或 $- 1$

查看试题解析
4. 若 $a$ 是方程 $x^{2} + x - 1 = 0$ 的根，则 $3 a^{2} + 3 a + 2024$ 的值为（）

A、2021 B、2024 C、2027 D、2030

查看试题解析
5. 用配方法解方程x²-4x-3=0，则配方正确的是（）

A、(x-2)²=1 B、(x+2)²=1 C、(x-2)²=7 D、(x+2)²=7

查看试题解析
6. 已知关于x的方程 $a (x - m)^{2} + k = 0$ （a，m，k均为常数，且 $a \neq 0$ ）的两个解是 $x_{1} = 1$ ， $x_{2} = 4$ ，则方程 $a (x - m - 2)^{2} + k = 0$ 的解是（）.

A、 $x_{1} = 1$ ， $x_{2} = - 2$ B、 $x_{1} = 3$ ， $x_{2} = 6$ C、 $x_{1} = 1$ ， $x_{2} = 4$ D、 $x_{1} = - 1$ ， $x_{2} = 2$

查看试题解析
7. 用直接开平方法解下列一元二次方程，其中无解的方程为（）

A、 $x^{2} = 0$ B、 $x^{2} - 2 = 0$ C、 $- x^{2} + 2 = 0$ D、 $x^{2} + 2 = 0$

查看试题解析
8. 在用求根公式 $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ 求一元二次方程的根时，小南正确地代入了a，b，c 得到 $x = \frac{3 \pm \sqrt{(- 3)^{2} - 4 \times 2 \times (- 1)}}{2 \times 2}$ ，则他求解的一元二次方程是（）

A、 $2 x^{2} - 3 x - 1 = 0$ B、 $2 x^{2} + 4 x - 1 = 0$ C、 $- x^{2} - 3 x + 2 = 0$ D、 $3 x^{2} - 2 x + 1 = 0$

查看试题解析
9. 若关于 $x$ 的一元二次方程 $(k - 1) x^{2} - 2 k x + k - 3 = 0$ 有实数根，则 $k$ 的取值范围为（）

A、 $k \geq \frac{3}{4}$ B、 $k \geq \frac{3}{4}$ 且 $k \neq 1$ C、 $k \geq 0$ D、 $k \geq 0$ 且 $k \neq 1$

查看试题解析
10. 设x₁ ， x₂是关于x的一元二次方程x²-7x-4m²=0的两个不同实数根，则x₁+x₂的值是（）

A、-4 B、4 C、7 D、-7

查看试题解析
11. 某工厂第二季度的产值比第一季度的产值增长了x%，第三季度的产值又比第二季度的产值增长了x%，则第三季度的产值比第一季度增长了（）

A、2x% B、1+2x% C、（1+x%）·x% D、（2+x%）·x%

查看试题解析
12. 小聪、小明、小伶、小刚四人共同探究代数式 $2 x^{2} - 4 x + 6$ 的值的情况他们做了如下分工：小聪负责找值为0时x的值，小明负责找值为4时x的值，小伶负责找最小值，小明负责找最大值，几分钟后，各自通报探究的结论，其中正确的是（）
（1）小聪认为找不到实数x，使 $2 x^{2} - 4 x + 6$ 得值为0；
（2）小明认为只有当 $x = 1$ 时， $2 x^{2} - 4 x + 6$ 的值为4；
（3）小伶发现 $2 x^{2} - 4 x + 6$ 没有最小值；
（4）小刚发现 $2 x^{2} - 4 x + 6$ 没有最大值．

A、（1）（2） B、（1）（3） C、（1）（2）（4） D、（2）（3）（4）

查看试题解析

二、填空题：本大题共4小题，每小题4分，共16分.只要求填出最后结果.

13. 设x₁ ， x₂是一元二次方程x²-2x-1=0的两根，则 $x_{1}^{} + x_{2}^{} + x_{1}^{} x_{2}^{} =$ .

查看试题解析
14. 已知等腰三角形的两边长分别是一元二次方程x²-6x+8＝0的两根，则该三角形的周长为．

查看试题解析
15. 如图，某小区规划在一个长为40 m、宽为26 m 的长方形场地 ABCD上修建三条同样宽的通道，使其中两条与AB平行，另一条与AD平行，其余部分种花草.要使每一块草坪的面积都为144 m² ，求通道的宽.若设通道的宽为 x m，请补全关于x的方程：(40-2x)()=144×6.

查看试题解析
16. 南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题：“直田积八百六十四步，只云阔与长共六十步，问阔及长各几步?”其大意是：矩形面积为八百六十四平方步，宽和长共六十步，问宽和长各几步?若设宽为x步，则根据题意可列方程为．

查看试题解析

三、解答题：本大题共7小题，共68分.

17. 解下列方程：

(1)、 $x^{2} + 8 x - 9 = 0$

(2)、 $x^{2} - 6 x + 4 = 0$

查看试题解析
18. 已知关于 $x$ 的方程 $x^{2} - 2 x + k - 1 = 0$ 有两个实数根．

(1)、求 $k$ 的取值范围；

(2)、若 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} = x_{1}^{2} + 2 x_{2} - 1$ ，求 $k$ 的值．

查看试题解析
19. 已知方程x²+bx+a＝0①，和方程ax²+bx+1＝0②（a≠0）．
（1）若方程①的根为x₁＝2，x₂＝3，求方程②的根；
（2）当方程①有一根为x＝r时，求证x＝ $\frac{1}{r}$ 是方程②的根；
（3）若a²b+b＝0，方程①的根是m与n，方程②的根是s和t，求 $\frac{m s}{n t}$ 的值．

查看试题解析
20. 【阅读材料】把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．配方法在代数式求值、解方程、最值问题中都有着广泛的应用．
例如：①用配方法因式分解： $a^{2} + 6 a + 8$ ． ②求 $x^{2} + 6 x + 11$ 的最小值．
解：原式 $= a^{2} + 6 a + 9 - 1$
$= {(a + 3)}^{2} - 1^{2}$
$= (a + 3 - 1) (a + 3 + 1)$
$= (a + 2) (a + 4)$ ；
解：原式 $= x^{2} + 6 x + 9 + 2$
$= {(x + 3)}^{2} + 2$ ；
$∵ {(x + 3)}^{2} \geq 0$ ，
$∴ {(x + 3)}^{2} + 2 \geq 2$ ，
即 $x^{2} + 6 x + 11$ 的最小值为2．
请根据上述材料解决下列问题：

(1)、当 $x$ 为何值时，多项式 $x^{2} + 4 x - 6$ 有最小值？请求出这个最小值；

(2)、若 $x^{2} + 5 x + 2 = 0$ ，求 $2 x^{2} + 11 x - \frac{10}{2 + x^{2}}$ 的值；

(3)、证明：关于 $x$ 的二次三项式 $x^{2} + 8 x + 20$ 在实数范围内不能因式分解．

查看试题解析
21. 用一张长为40cm，宽为25cm的长方形硬纸片，裁去一部分后折成纸盒。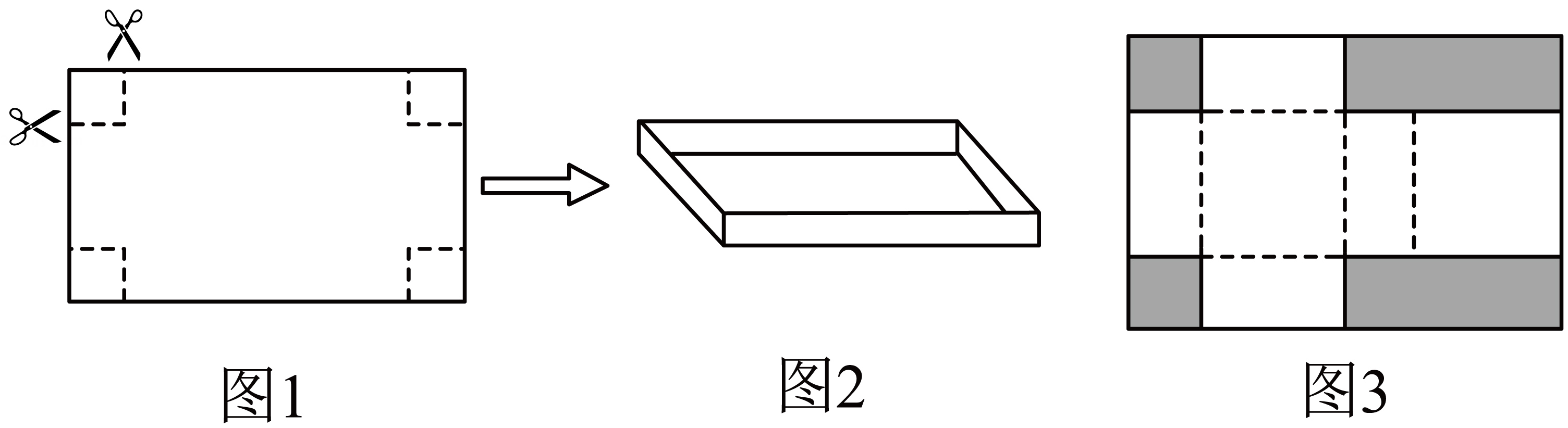

(1)、如图1裁去角上四个小正方形之后，折成如图2的无盖纸盒。若纸盒底面积为450cm² ，则纸盒的高是多少？

(2)、如图3，在纸片左边的两个角裁去两个正方形，纸片右边的两个角裁去两个长方形之后，将剩下的纸片（空白部分）折成一个有盖的纸盒。若折成纸盒的表面积为912cm² ，则裁去的正方形的边长是多少？

查看试题解析
22. 如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根是另一个根的 $n$ 倍 $(n$ 为正整数），则称这样的方程为“ $n$ 倍根方程”．例如：方程 $x^{2} - 6 x + 8 = 0$ 的两个根分别是2和4，则这个方程就是“二倍根方程”；方程 $x^{2} - 4 x + 3 = 0$ 的两个根分别是1和3，则这个方程就是“三倍根方程”．

(1)、根据上述定义， $2 x^{2} - 5 x + 2 = 0$ 是“________倍根方程”；

(2)、若关于 $x$ 的方程 $x^{2} + 6 x + m = 0$ 是“三倍根方程”，求 $m$ 的值；

(3)、直线 $l_{1}$ ： $y = - x + 5$ 与 $x$ 轴交于点 $A$ ，直线 $l$ 过点 $B (- 1, 0)$ ，且与 $l_{1}$ 相交于点 $C (1, 4)$ ．若一个五倍根方程的两个根为 $x_{1}$ 和 $x_{2} (0 < x_{1} < x_{2})$ ，且点 $P (x_{1}, x_{2})$ 在 $△ A B C$ 的内部（不包含边界），求 $x_{1}$ 的取值范围．

查看试题解析
23. 综合与实践：洗衣粉售价方案设计
某厂家生产的一种洗衣粉采用A、B两种包装，当前销售的相关信息如下表：
包装规格
$A$
$B$
含量（千克／袋）
2
1
成本（元／袋）
10
5
售价（元／袋）
25
17
日销量（袋）
60
40
该厂家经市场调研发现适当提升 $A$ 包装洗衣粉售价可以增加每日利润，已知售价每提升1元会少卖2袋。一段时间后，由于产能下降，厂家决定每日定额生产150千克的洗衣粉（当日全部售出）。另外厂家下调了 $B$ 包装洗衣粉的售价，已知其售价每降低1元会多卖2袋。
根据以上信息解决问题：
设 $A$ 包装洗衣粉每袋售价提高 $x$ 元（ $x > 0$ ）。

(1)、问该厂家每日销售 $A$ 包装洗衣粉的利润能否达到1000元？若能，请求出 $A$ 包装洗衣粉的售价；若不能，请说明理由．

(2)、当厂家每日定额产销150千克洗衣粉时，设 $B$ 包装洗衣粉每袋售价降低 $y$ 元（ $y > 0$ ）。
①求 $y$ 关于 $x$ 的函数关系．
②请通过计算判断厂家销售两种包装洗衣粉的日总利润能否达到1450元？

查看试题解析

包装规格	$A$	$B$
含量（千克／袋）	2	1
成本（元／袋）	10	5
售价（元／袋）	25	17
日销量（袋）	60	40