带电粒子在磁场中的运动(高考真题组)
试卷更新日期:2017-12-19 类型:二轮复习
一、单选题
-
1.
平面OM和平面ON之间的夹角为30°,其横截面(纸面)如图所示,平面OM上方存在匀强磁场,磁感应强度大小为B,方向垂直于纸面向外。一带电粒子的质量为m,电荷量为q(q>0)。粒子沿纸面以大小为v的速度从PM的某点向左上方射入磁场,速度与OM成30°角。已知粒子在磁场中的运动轨迹与ON只有一个交点,并从OM上另一点射出磁场。不计重力。粒子离开磁场的射点到两平面交线O的距离为 ()
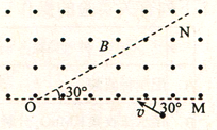 A、 B、 C、 D、2.
A、 B、 C、 D、2.如图,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P为磁场边界上的一点,大量相同的带电粒子以相同的速率经过P点,在纸面内沿不同方向射入磁场,若粒子射入的速率为v1 , 这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为v2 , 相应的出射点分布在三分之一圆周上,不计重力及带电粒子之间的相互作用,则v2:v1为( )
 A、:2 B、:1 C、:1 D、3:3.
A、:2 B、:1 C、:1 D、3:3.一圆筒处于磁感应强度大小为B的匀强磁场中,磁场方向与筒的轴平行,筒的横截面如图所示.图中直径MN的两端分别开有小孔,筒绕其中心轴以角速度ω顺时针转动.在该截面内,一带电粒子从小孔M射入筒内,射入时的运动方向与MN成30°角.当筒转过90°时,该粒子恰好从小孔N飞出圆筒.不计重力.若粒子在筒内未与筒壁发生碰撞,则带电粒子的比荷为( )
 A、 B、 C、 D、4.
A、 B、 C、 D、4.如图,在两水平极板间存在匀强电场和匀强磁场,电场方向竖直向下,磁场方向垂直于纸面向里.一带电粒子以某一速度沿水平直线通过两极板.若不计重力,下列四个物理量中哪一个改变时,粒子运动轨迹不会改变?( )
 A、粒子速度的大小 B、粒子所带的电荷量 C、电场强度 D、磁感应强度5. 在粒子散射实验中,电子对粒子运动的影响可以忽略,这是因为与粒子相比,电子( )A、电量太小 B、速度太小 C、体积太小 D、质量太小6.
A、粒子速度的大小 B、粒子所带的电荷量 C、电场强度 D、磁感应强度5. 在粒子散射实验中,电子对粒子运动的影响可以忽略,这是因为与粒子相比,电子( )A、电量太小 B、速度太小 C、体积太小 D、质量太小6.如图所示,S处有一电子源,可向纸面内任意方向发射电子,平板MN垂直于纸面,在纸面内的长度L=9.1cm,中点O与S间的距离d=4.55cm,MN与SO直线的夹角为θ,板所在平面有电子源的一侧区域有方向垂直于纸面向外的匀强磁场,磁感应强度B=2.0×10-4T,电子质量m=9.1×10-31kg,电荷量e=-1.6×10-19C,不计电子重力。电子源发射速度v=1.6×106m/s的一个电子,该电子打在板上可能位置的区域的长度为l,则( )
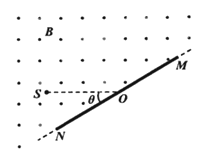 A、θ=90°时,l=9.1cm B、θ=60°时,l=9.1cm C、θ=45°时,l=4.55cm D、θ=30°时,l=4.55cm7.
A、θ=90°时,l=9.1cm B、θ=60°时,l=9.1cm C、θ=45°时,l=4.55cm D、θ=30°时,l=4.55cm7.图中曲线a、b、c、d为气泡室中某放射物质发生衰变放出的部分粒子的径迹,气泡室中磁感应强度方向垂直纸面向里。以下判断可能正确的是( )
 A、a、b为β粒子的径迹 B、a、b为γ粒子的径迹 C、c、d为α粒子的径迹 D、c、d为β粒子的径迹8.
A、a、b为β粒子的径迹 B、a、b为γ粒子的径迹 C、c、d为α粒子的径迹 D、c、d为β粒子的径迹8.现代质谱仪可用来分析比质子重很多的离子,其示意图如图所示,其中加速电压恒定.质子在入口处从静止开始被加速电场加速,经匀强磁场偏转后从出口离开磁场.若某种一价正离子在入口处从静止开始被同一加速电场加速,为使它经匀强磁场偏转后仍从同一出口离开磁场,需将磁感应强度增加到原来的12倍.此离子和质子的质量比约为( )
 A、11 B、12 C、121 D、144
A、11 B、12 C、121 D、144二、综合题
-
9.
如图所示,直径分别为D和2D的同心圆处于同一竖直面内,O为圆心,GH为大圆的水平直径。两圆之间的环形区域(Ⅰ区)和小圆内部(Ⅱ区)均存在垂直圆面向里的匀强磁场。间距为d的两平行金属极板间有一匀强电场,上极板开有一小孔。一质量为m,电量为+q的粒子由小孔下方d/2处静止释放,加速后粒子以竖直向上的速度v射出电场,由点紧靠大圆内侧射入磁场。不计粒子的重力。
 (1)、求极板间电场强度的大小;(2)、若粒子运动轨迹与小圆相切,求区磁感应强度的大小;(3)、若Ⅰ区,Ⅱ区磁感应强度的大小分别为2mv/qD,4mv/qD,粒子运动一段时间后再次经过H点,求这段时间粒子运动的路程。10.
(1)、求极板间电场强度的大小;(2)、若粒子运动轨迹与小圆相切,求区磁感应强度的大小;(3)、若Ⅰ区,Ⅱ区磁感应强度的大小分别为2mv/qD,4mv/qD,粒子运动一段时间后再次经过H点,求这段时间粒子运动的路程。10.现代科学仪器常利用电场、磁场控制带电粒子的运动。在真空中存在着如图所示的多层紧密相邻的匀强电场和匀强磁场,电场和磁场的宽度均为 。电场强度为 , 方向水平向右;磁感应强度为 , 方向垂直纸面向里。电场、磁场的边界互相平行且与电场方向垂直,一个质量为 、电荷量为 的带正电粒子在第1层电场左侧边界某处由静止释放,粒子始终在电场、磁场中运动,不计粒子重力及运动时的电磁辐射
 (1)、求粒子在第2层磁场中运动时速度的大小与轨迹半径(2)、粒子从第层磁场右侧边界穿出时,速度的方向与水平方向的夹角为 , 试求(3)、若粒子恰好不能从第层磁场右侧边界穿出,试问在其他条件不变的情况下,也进入第层磁场,但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明之11.
(1)、求粒子在第2层磁场中运动时速度的大小与轨迹半径(2)、粒子从第层磁场右侧边界穿出时,速度的方向与水平方向的夹角为 , 试求(3)、若粒子恰好不能从第层磁场右侧边界穿出,试问在其他条件不变的情况下,也进入第层磁场,但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明之11.如图所示,空间中存在着水平向右的匀强电场,电场强度大小为E=5 N/C,同时存在着水平方向的匀强磁场,其方向与电场方向垂直,磁感应强度大小B=0.5T。有一带正电的小球,质量m=1.0×10-6kg,电荷量q=2×10-6C,正以速度v在图示的竖直面内做匀速直线运动,当经过P点时撤掉磁场(不考虑磁场消失引起的电磁感应现象)取g=10m/s2 , 求
 (1)、小球做匀速直线运动的速度v的大小和方向;(2)、从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t。12.
(1)、小球做匀速直线运动的速度v的大小和方向;(2)、从撤掉磁场到小球再次穿过P点所在的这条电场线经历的时间t。12.如图所示,图面内有竖直线DD',过DD'且垂直于图面的平面将空间分成I、II两区域。区域I有方向竖直向上的匀强电场和方向垂直图面的匀强磁场B(图中未画出);区域II有固定在水平面上高 h=2l 、倾角 的光滑绝缘斜面,斜面顶端与直线DD'距离 s=4l ,区域II可加竖直方向的大小不同的匀强电场(图中未画出);C点在DD'上,距地面高 H=3l 。零时刻,质量为m、带电荷量为q的小球P在K点具有大小 、方向与水平面夹角 的速度,在区域I内做半径 的匀速圆周运动,经C点水平进入区域II。某时刻,不带电的绝缘小球A由斜面顶端静止释放,在某处与刚运动到斜面的小球P相遇。小球视为质点,不计空气阻力及小球P所带电量对空间电磁场的影响。l已知,g为重力加速度。
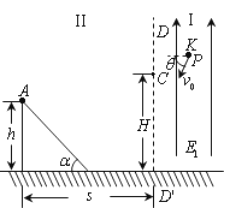 (1)、求匀强磁场的磁感应强度的大小;(2)、若小球A、P在斜面底端相遇,求释放小球A的时刻tA;(3)、若小球A、P在时刻 (β为常数)相遇于斜面某处,求此情况下区域II的匀强电场的场强E,并讨论场强E的极大值和极小值及相应的方向。13.
(1)、求匀强磁场的磁感应强度的大小;(2)、若小球A、P在斜面底端相遇,求释放小球A的时刻tA;(3)、若小球A、P在时刻 (β为常数)相遇于斜面某处,求此情况下区域II的匀强电场的场强E,并讨论场强E的极大值和极小值及相应的方向。13.题9图为某种离子加速器的设计方案.两个半圆形金属盒内存在相同的垂直于纸面向外的匀强磁场.其中和是间距为的两平行极板,其上分别有正对的两个小孔和 , , 为靶点,(为大于1的整数).极板间存在方向向上的匀强电场,两极板间电压为.质量为、带电量为的正离子从点由静止开始加速,经进入磁场区域.当离子打到极板上区域(含点)或外壳上时将会被吸收.两虚线之间的区域无电场和磁场存在,离子可匀速穿过.忽略相对论效应和离子所受的重力.求:
 (1)、离子经过电场仅加速一次后能打到点所需的磁感应强度大小;(2)、能使离子打到P点的磁感应强度的所有可能值;(3)、打到P点的能量最大的离子在磁场中运动的时间和在电场中运动的时间。14.
(1)、离子经过电场仅加速一次后能打到点所需的磁感应强度大小;(2)、能使离子打到P点的磁感应强度的所有可能值;(3)、打到P点的能量最大的离子在磁场中运动的时间和在电场中运动的时间。14.使用回旋加速器的实验需要把离子束从加速器中引出,离子束引出的方法有磁屏蔽通道法和静电偏转法等。质量为m,速度为v的离子在回旋加速器内旋转,旋转轨道时半径为r的圆,圆心在O点,轨道在垂直纸面向外的匀强磁场中,磁感应强度为B。为引出离子束,使用磁屏蔽通道法设计引出器。引出器原理如图所示,一堆圆弧形金属板组成弧形引出通道,通道的圆心位于O'点(O' 点图中未画出)。引出离子时,令引出通道内磁场的磁感应强度降低,从而使离子从P点进入通道,沿通道中心线从Q点射出。已知OQ长度为L。OQ与OP的夹角为θ,
 (1)、求离子的电荷量q并判断其正负;(2)、离子从P点进入,Q点射出,通道内匀强磁场的磁感应 强度应降为B',求B';(3)、换用静电偏转法引出离子束,维持通道内的原有磁感应强度B不变,在内外金属板间加直流电压,两板间产生径向电场,忽略边缘效应。为使离子仍从P点进入,Q点射出,求通道内引出轨迹处电场强度E 的方向和大小。
(1)、求离子的电荷量q并判断其正负;(2)、离子从P点进入,Q点射出,通道内匀强磁场的磁感应 强度应降为B',求B';(3)、换用静电偏转法引出离子束,维持通道内的原有磁感应强度B不变,在内外金属板间加直流电压,两板间产生径向电场,忽略边缘效应。为使离子仍从P点进入,Q点射出,求通道内引出轨迹处电场强度E 的方向和大小。三、计算题
-
15.
如图,空间存在方向垂直于纸面(xOy平面)向里的磁场.在x≥0区域,磁感应强度的大小为B0;x<0区域,磁感应强度的大小为λB0(常数λ>1).一质量为m、电荷量为q(q>0)的带电粒子以速度v0从坐标原点O沿x轴正向射入磁场,此时开始计时,当粒子的速度方向再次沿x轴正向时,求(不计重力)
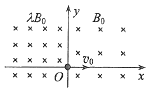 (1)、粒子运动的时间;(2)、粒子与O点间的距离.16.
(1)、粒子运动的时间;(2)、粒子与O点间的距离.16.回旋加速器的工作原理如题15-1图所示,置于真空中的D形金属盒半径为R,两盒间狭缝的间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子的质量为m,电荷量为+q,加在狭缝间的交变电压如题15-2图所示,电压值的大小为Ub。周期T= 。一束该粒子在t=0- 时间内从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:

①出折粒子的动能 ;②粒子从飘入狭缝至动能达到 所需的总时间
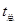 ;
;③要使飘入狭缝的粒子中有超过99%能射出,d应满足的条件.
17.平面直角坐标系xOy中,第Ⅰ象限存在垂直于平面向里的匀强磁场,第Ⅲ现象存在沿y轴负方向的匀强电场,如图所示。一带负电的粒子从电场中的Q点以速度v0沿x轴正方向开始运动,Q点到y轴的距离为到x轴距离的2倍。粒子从坐标原点O离开电场进入电场,最终从x轴上的P点射出磁场,P点到y轴距离与Q点到y轴距离相等。不计粒子重力,为:
 (1)、粒子到达O点时速度的大小和方向;(2)、电场强度和磁感应强度的大小之比。18.
(1)、粒子到达O点时速度的大小和方向;(2)、电场强度和磁感应强度的大小之比。18.一台质谱仪的工作原理如图所示.大量的甲、乙两种离子飘入电压力为U0的加速电场,其初速度几乎为0,经过加速后,通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片上.已知甲、乙两种离子的电荷量均为+q,质量分别为2m和m,图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹.不考虑离子间的相互作用.
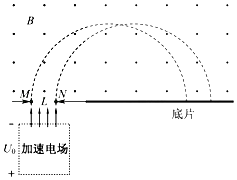 (1)、求甲种离子打在底片上的位置到N点的最小距离x;(2)、在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;(3)、若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.
(1)、求甲种离子打在底片上的位置到N点的最小距离x;(2)、在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;(3)、若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.