北京版七（下）数学第五章二元一次方程组单元测试提升卷

试卷更新日期：2026-01-06 类型：单元试卷

进入出卷网下载

一、选择题（每题2分，共16分）

1. 对于方程 $x + 3 y = 2$ ，用含x的代数式表示y，正确的是（）

A、 $x = 3 y - 2$ B、 $x = 2 - 3 y$ C、 $y = \frac{x - 2}{3}$ D、 $y = \frac{2 - x}{3}$

查看试题解析
2. 若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c . \end{array}$ 的解为 ${\begin{array}{l} x = 4 \\ y = 6 \end{array}$ ，则方程组 ${\begin{array}{l} 4 a_{1} x + 3 b_{1} y = 5 c_{1} \\ 4 a_{2} x + 3 b_{2} y = 5 c_{2} \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 4 \\ y = 6 \end{array}$ B、 ${\begin{array}{l} x = 5 \\ y = 6 \end{array}$ C、 ${\begin{array}{l} x = 5 \\ y = 10 \end{array}$ D、 ${\begin{array}{l} x = 20 \\ y = 30 \end{array}$

查看试题解析
3. 若方程组 ${\begin{array}{l} 2 x + k y = 6, \\ x - 2 y = 0 \end{array}$ 有正整数解，则 $k$ 的正整数值应为（）

A、1 B、2 C、3 D、不存在

查看试题解析
4. 如果某个二元一次方程组的解中两个未知数的值是互为相反数，我们称这个方程组为“关联方程组”.若关于x，y的方程组 ${\begin{array}{l} x + 3 y = 4 - a \\ x - y = 3 a \end{array}$ 是“关联方程组”，则a的值为（）

A、0 B、1 C、2 D、-2

查看试题解析
5. 三元一次方程组 ${\begin{array}{l} x - y = 1 \\ y - z = 1 \\ x + z = 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 2 \\ y = 3 \\ z = 4 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 4 \\ z = 3 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = 2 \\ z = 4 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 3 \\ z = 2 \end{array}$

查看试题解析
6. 我国古代数学名著《九章算术》中记载：“今有甲、乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而钱亦五十，问甲、乙持钱各几何？”题目大意是：今有甲、乙二人，不知其钱包里有多少钱，若乙把其一半的钱给甲，则甲的钱数为50；而甲把其 $\frac{2}{3}$ 的钱给乙，则乙的钱数也能为50，问甲、乙各有多少钱？若设甲持钱为x，乙持钱为y，则下列方程组中正确的是（）

A、 ${\begin{array}{l} \frac{1}{2} x + y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$ B、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + x = 50 \end{array}$ C、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ \frac{2}{3} y + x = 50 \end{array}$ D、 ${\begin{array}{l} x + \frac{1}{2} y = 50 \\ y + \frac{2}{3} x = 50 \end{array}$

查看试题解析
7. 已知x，y满足方程组 ${\begin{array}{l} 3 x - y = 5 - 2 m \\ x - 2 y = m \end{array}$ ，则无论m取何值，x，y恒有关系式是（）

A、 $4 x - 3 y = 5$ B、 $2 x + y = 5$ C、 $x - y = 1$ D、 $x + 3 y = 5$

查看试题解析
8. 已知关于x，y的二元一次方程组 ${\begin{array}{l} x + 3 y = 8 - a, \\ x - y = 3 a, \end{array}$ 给出下列结论中，正确的是（）
①当这个方程组的解x，y的值互为相反数时， $a = - 4$ ；
②当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 + 2 a$ 的解；
③无论 $a$ 取什么实数， $x + 2 y$ 的值始终不变；
④若用 $x$ 表示 $y$ ，则 $y = - \frac{x}{2} + 3$ ．

A、①② B、②③ C、②③④ D、①③④

查看试题解析

二、填空题（每题2分，共16分）

9. 写一个解为 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 的二元一次方程．

查看试题解析
10. 已知， $x = 3$ 、 $y = 2$ 是方程组 $\{\begin{array}{l} 6 x + b y = 32 \\ a x - b y = 4 \end{array}$ 的解，则 $a - b =$ ．

查看试题解析
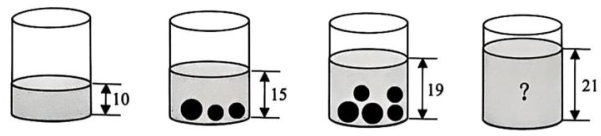
11. 已知 ${\begin{array}{l} a m^{2} + b m + c = n \\ a n^{2} + b n + c = m \end{array}$ ，其中m ， n为互不相等实数，且满足 $m + n = 3$ ，则 $b =$ ．（结果用只含a的代数式表示）

查看试题解析
12. 一个圆柱形容器中装有一定量的水，放入若干个大铁球和小铁球后（假设所有球都浸没在水中），水面上升情况如图所示，要使水面高度为21，则可以放入个大铁球和个小铁球.（写出一组符合要求的值即可）

查看试题解析
13. 关于x，y的二元一次方程ax+by=c（a，b，c为常数）， b=a+1 ，c=b+1，对任意一个满足条件的a，此二元一次方程都有一个公共解，则这个公共解为.

查看试题解析
14. 已知方程组 $\{\begin{matrix} 2 x - y = 2 \\ x - 2 y = m \end{matrix}$ ，若 $x$ 与 $y$ 的和为4，则 $m$ 的值为．

查看试题解析
15. 已知 $\{\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，是二元一次方程组 $\{\begin{matrix} a x + b y = 7, \\ a x - b y = 1 \end{matrix}$ 的解，则 $6 a - b$ 的值为．

查看试题解析
16. 如图，在一个大长方形中放入六个形状、大小相同的小长方形，有关尺寸如图所示，则图中大长方形ABCD的面积是cm²

查看试题解析

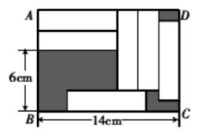
三、解答题（共12题，共68分）

17. 解方程（组）

(1)、 $3 (x - 2) + 1 = x - (2 x - 1)$

(2)、 $\{\begin{array}{l} 2 x - y = 5 \\ 4 x + 3 y = - 10 \end{array}$

查看试题解析
18. 解二元一次方程组 ${\begin{array}{l} 2 x = 3 y + 1, & ① \\ 4 x + y = 9 . & ② \end{array}$ 时，两位同学的部分解答过程如下：
圆圆：由②，得 $y = 9 - 4 x$ ③（依据： ▲ ）
把③代入①，得 $2 x = 3 (9 - 4 x) + 1$
芳芳：把①代入②，得2（ ▲ ） $+ y = 9$ ．

(1)、补全上述空白部分内容；

(2)、请选择一种你喜欢的方法完成解答．

查看试题解析
19. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x + 3 y = 2 k + 4 \\ x - 2 y = k \end{array}$

(1)、若方程组的解互为相反数，求 $k$ 的值

(2)、若方程组的解满足方程 $3 x + y = 10$ ，求 $k$ 的值.

查看试题解析
20. 已知下列五对数值：
$① \{\begin{matrix} x = - 8 ， \\ y = - 10 ； \end{matrix} ② \{\begin{matrix} x = 0 ， \\ y = - 6 ； \end{matrix} ③ \{\begin{matrix} x = 10 ， \\ y = - 1 ； \end{matrix} ④ \{\begin{matrix} x = 41 ， \\ y = - 3 ； \end{matrix} ⑤ \{\begin{matrix} x = - 21 ， \\ y = 1 ． \end{matrix}$

(1)、哪几对数值是方程 $\frac{1}{2} x - y = 6$ 的解?

(2)、哪几对数值是方程2 $x$ +31y=-11的解?

(3)、直接写出方程组 $\{\begin{matrix} \frac{1}{2} x - y = 6 \\ 2 x + 31 y = - 11 \end{matrix}$ 的解.

查看试题解析
21. 2025年国家卫健委建议实施“体重管理年”三年行动 $.$ 某校要组织学生外出研学，根据营养师的建议准备了A，B两种食品作为午餐A餐每包的热量为700千焦，蛋白质为5克.B餐每包热量为800千焦，蛋白质为10克。

(1)、若要从这两种食品中摄入3700千焦热量和35克蛋白质，应选用A，B两种食品各多少包？

(2)、运动量大的人或青少年对蛋白质的摄入量应更多.若每份午餐选用这两种食品共7包，要使每份午餐中的蛋白质含量不低于55克，且热量最低，应如何选用这两种食品？

查看试题解析
22. 身体每天消耗的热量主要由碳水化合物和脂肪（不考虑蛋白质及其他有机物）提供．碳水化合物和脂肪分解时所消耗的氧气、生成的二氧化碳、释放的热量三个方面的相关数据如下表：
分解的营养物质
氧气消耗量/克
二氧化碳生成量/克
释放热量/千焦
1克碳水化合物
1
1.5
15
1克脂肪
3
3
45
请解答下列问题：

(1)、研究人员测出小祺在某次运动中平均每分钟消耗氧气2.5克，产生二氧化碳3克，求小祺的身体平均每分钟分解碳水化合物与脂肪各多少克．

(2)、已知小祺骑脚踏车每分钟消耗热量20千焦，快走每分钟消耗热量27千焦，小祺某天骑脚踏车和快走共1小时，若要消耗完40克碳水化合物与20克脂肪分解后释放的热量，小祺至少需要分配多少分钟进行快走？（精确到1分钟）

查看试题解析
23. 我校到商场购买A、B两种品牌的足球，购买A种品牌的足球20个，B种品牌的足球30个，共花费4600元，已知购买4个B种品牌的足球与购买5个A种品牌的足球费用相同．

(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元；

(2)、学校为了响应习总书记“足球进校园”的号召，我校决定再次购进A、B两种品牌足球共42个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高5元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的80%，且保证这次购买的B品牌足球不少于20个，则这次学校有哪几种购买方案？

(3)、为了节约资金，学校应选择哪种方案？请你求出学校在第二次购买活动中最少需要多少资金？

查看试题解析
24. 在纸盒制作的劳动实践课上，对规格是150cm×90cm的原材料板材进行裁剪得到A型长方形纸板和B型正方形纸板.为了避免材料浪费，每张原材料板材先裁得3张150cm×30cm的纸板条，每张纸板条又恰好可以裁得3张A型长方形纸板或5张B型正方形纸板，如图1所示.（单位：cm）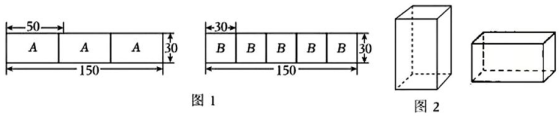

(1)、每张原材料板材可以裁得A型纸板张或裁得B型纸板张：

(2)、现有260张原材料板材全部裁剪（每张原材料板材只能一种裁法）得到A型与B型纸板当侧面和底面，做成如图2所示的竖式无盖长方体纸盒和横式无盖长方体纸盒，若横式无盖长方体纸盒个数为竖式无盖长方体纸盒个数的两倍，问：怎样裁剪才能使剪出的A，B型纸板恰好用完，两种纸盒各做多少个？

查看试题解析
25. 已知方程 $2 x - 3 = 1$ 与不等式 $x + 3 > 0$ ，当 $x = 2$ 时， $2 x - 3 = 2 \times 2 - 3 = 1$ ， $x + 3 = 2 + 3 = 5 > 0$ 同时成立，则称“ $x = 2$ ”是方程 $2 x - 3 = 1$ 与不等式 $x + 3 > 0$ 的“完美解”.

(1)、已知① $2 x + 1 > 3$ ， ② $2 - x > 2 x + 1$ ，则方程 $2 x + 3 = 1$ 的解是不等式（填序号）的“完美解”；

(2)、若 $\{\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 是方程组 $\{\begin{matrix} x + 2 y = a \\ 2 x + y = 2 a + 3 \end{matrix}$ 与不等式 $x + y > 1$ 的一组“完美解”，求a的取值范围；

(3)、若 $\{\begin{array}{l} x = x_{0} \\ y = y_{0} \end{array}$ 是方程 $x - 3 y = 5$ 与不等式组 $\{\begin{array}{l} x > 2 \\ y < 1 \end{array}$ 的“完美解”，求 $x_{0} + y_{0}$ 的取值范围.

查看试题解析
26. 阅读下列材料：为了提高全县学生的运算能力和解题技巧，李老师设计了如下的题目：
解方程 $\{\begin{array}{l} \frac{2 x + 3 y}{4} + \frac{2 x - 3 y}{3} = 7 \\ \frac{2 x + 3 y}{3} + \frac{2 x - 3 y}{2} = 8 \end{array}$ ，王栋同学发现如果直接用代入消元法或加减消元法求解，运算量比较大，也容易出错.如果把方程组中的 $2 x + 3 y$ 看作一个数，把 $2 x - 3 y$ 看作一个数，通过换元，可以解决问题.下面是他的解题过程：令 $m = 2 x + 3 y$ ， $n = 2 x - 3 y$ ，这时方程组可化为 $\{\begin{array}{l} \frac{m}{4} + \frac{n}{3} = 7 \\ \frac{m}{3} + \frac{n}{2} = 8 \end{array}$ 解得 $\{\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ ，把 $\{\begin{array}{l} m = 60 \\ n = - 24 \end{array}$ 代入 $m = 2 x + 3 y$ ， $n = 2 x - 3 y$ 得 $\{\begin{array}{l} 2 x + 3 y = 60 \\ 2 x - 3 y = - 24 \end{array}$ ，解得 $\{\begin{array}{l} x = 9 \\ y = 14 \end{array}$ ，

(1)、在解二元一次方程组时，我们的基本思路是“消元”，即通过“代入法”或“加减法”将“二元”化为“一元”，在“消元”的过程体现的数学思想是（）
A.数形结合思想 B.转化思想 C.分类讨论思想 D.类比思想

(2)、请你参考王栋同学的做法，解决下面的问题：解方程组 $\{\begin{array}{l} \frac{x + y}{6} + \frac{x - y}{10} = 3 \\ \frac{x + y}{6} - \frac{x - y}{10} = - 1 \end{array}$

查看试题解析
27. 某体育用品商场销售A，B两款足球，售价和进价如表所示：
类型
进价／（元／个）
售价／（元／个）
$A$ 款
$m$
120
$B$ 款
$n$
90
若该商场购进4个 $A$ 款足球和11个 $B$ 款足球需980元；购进2个 $A$ 款足球和3个 $B$ 款足球需340元．

(1)、求 $m$ 和 $n$ 的值．

(2)、某校在该商场一次性购买 $A$ 款足球 $x$ 个和 $B$ 款足球 $y$ 个，共消费3000元，那么该商场可获利多少元？

(3)、为了提高销量，商场实施：＂买足球送跳绳＂的促销活动：＂买1个 $A$ 款足球送1根跳绳，买3个 $B$ 款足球送2根跳绳＂，每根跳绳的成本为10元，某日售卖出两款足球总计盈利600元，那么该日商场销售A，B两款足球各多少个（每款都有销售）？

查看试题解析
28. 若关于x，y的二元一次方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解满足 $x = y$ ，则称此方程组为“等解”方程组。

(1)、关于x，y的方程组 ${\begin{array}{l} x + 2 y = 3, \\ m x + y = \frac{5}{2} \end{array}$ 为“等解”方程组，求m的值。

(2)、判断关于x，y的二元一次方程组 ${\begin{array}{l} a x + b y = c, \\ b x + a y = c \end{array}$ （a，b，c为常数，且 $a \neq - b$ ）是“等解”方程组吗？并说明理由.

查看试题解析

分解的营养物质	氧气消耗量/克	二氧化碳生成量/克	释放热量/千焦
1克碳水化合物	1	1.5	15
1克脂肪	3	3	45

类型	进价／（元／个）	售价／（元／个）
$A$ 款	$m$	120
$B$ 款	$n$	90

北京版七（下）数学第五章 二元一次方程组 单元测试提升卷

一、选择题（每题2分，共16分）

二、填空题（每题2分，共16分）

三、解答题（共12题，共68分）

北京版七（下）数学第五章二元一次方程组单元测试提升卷