北京版七（下）数学第五章二元一次方程组单元测试基础卷

试卷更新日期：2026-01-06 类型：单元试卷

进入出卷网下载

一、选择题（每题2分，共16分）

1. 下列属于二元一次方程的是（）

A、 $3 x + 5 = 0$ B、 $2 x - 3 y = 5$ C、 $x y = 9$ D、 $4 x - \frac{1}{y} = 7$

查看试题解析
2. 下列各方程组中，属于二元一次方程组的是（）

A、 ${\begin{array}{l} \frac{x}{3} - \frac{y}{2} = 1 \\ 3 x + 4 y = 2 \end{array}$ B、 ${\begin{array}{l} 2 x + y = 1 \\ x + z = 2 \end{array}$ C、 ${\begin{array}{l} 3 x + 2 y = 7 \\ x y = 5 \end{array}$ D、 ${\begin{array}{l} \frac{5}{x} + \frac{y}{3} = \frac{1}{2} \\ x + 2 y = 3 \end{array}$

查看试题解析
3. 用代入消元法解二元一次方程组 ${\begin{array}{l} y = x - 4 ① \\ 2 x + y = 2 ② \end{array}$ 时，将①代入②，得（）

A、 $2 x - x - 4 = 2$ B、 $2 x - x + 4 = 2$ C、 $2 x + x - 4 = 2$ D、 $2 x + x + 4 = 2$

查看试题解析
4. 用加减消元法解方程组 $\{\begin{matrix} 2 x + 3 y = - 1 ① \\ 3 x - 3 y = 4 ② \end{matrix}$ ，下列做法正确的是（）

A、要消去y， $① - ②$ B、要消去x， $① \times 3 + ② \times 2$ C、要消去y， $① + ②$ D、要消去x， $① \times 2 - ② \times 3$

查看试题解析
5. 以 ${\begin{cases} x = 3 \\ y = 1 \\ z = - 1 \end{cases}$ 为解建立三元一次方程组，不正确的是（）

A、 $3 x - 4 y + 2 z = 3$ B、 C、 $x + y - z = - 2$ D、 $\frac{x}{2} - \frac{2}{3} y - z = 1 \frac{5}{6}$

查看试题解析
6. 某班35名学生共种87棵树苗．其中男生每人种3棵，女生每人种2棵，该班男生有 $x$ 人，女生有 $y$ 人．根据题意，所列方程组正确的是（）

A、 $\{\begin{matrix} x + y = 87 \\ 3 x + 2 y = 35 \end{matrix}$ B、 $\{\begin{matrix} x + y = 87 \\ 2 x + 3 y = 35 \end{matrix}$ C、 $\{\begin{matrix} x + y = 35 \\ 2 x + 3 y = 87 \end{matrix}$ D、 $\{\begin{matrix} x + y = 35 \\ 3 x + 2 y = 87 \end{matrix}$

查看试题解析
7. 下列几组解中，二元一次方程 $x - y = 1$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$

查看试题解析
8. 《孙子算经》是中国传统数学的重要著作，其中有一道题，原文如下：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺.木长几何?”其大意是：用一根绳子去量一根木头的长，绳子还剩余4.5尺.将绳子对折再量木头，则木头还剩余1尺，问：木头长多少尺?可设木头长x尺，绳子长y尺，则所列方程组正确的是( )

A、 ${\begin{matrix} y - x = 4.5, \\ 2 x - y = 1 \end{matrix}$ B、 ${\begin{matrix} x - y = 4.5, \\ 2 x - y = 1 \end{matrix}$ C、 ${\begin{matrix} x - y = 4.5, \\ \frac{y}{2} - x = 1 \end{matrix}$ D、 ${\begin{matrix} y - x = 4.5, \\ x - \frac{y}{2} = 1 \end{matrix}$

查看试题解析

二、填空题（每题2分，共16分）

9. 若关于x、y的方程2x^a^-1+3y=1是二元一次方程，那么a=.

查看试题解析
10. 已知 $\{\begin{array}{l} x = a \\ y = 3 \end{array}$ 是方程 $2 x + 3 y = 5$ 的一个解，则 $a =$ ．

查看试题解析
11. 二元一次方程组 $\{\begin{matrix} x + 8 y = 10 \\ 5 x + 7 y = 9 \end{matrix}$ 用代入消元法消去未知数x，得到关于y的一元一次方程可以是．

查看试题解析
12. 已知关于x、y的方程组 $\{\begin{cases} 3 x + 5 y = k + 2 \\ 2 x + 3 y = k \end{cases}$ 的解满足x+y=2，k= ．

查看试题解析
13. 某商场出售甲、乙、丙三种型号的商品，若购买甲2件，乙3件，丙1件，共需130元；购买甲3件，乙5件，丙1件，共需205元．若购买甲，乙，丙各1件，则需元．

查看试题解析
14. 《水浒传》中关于神行太保戴宗有这样一段描述：程途八百里，朝去暮还来．某日，戴宗去160里之外的地方打探情报，去时顺风，用了2小时；回来时逆风，用了4小时，则戴宗在无风时的平均速度为里/小时．

查看试题解析
15. 首届“安海校园杯”足球赛火热进行中，足球是用黑白两种颜色的皮块缝制而成，如图所示，黑色皮块是正五边形，白色皮块是正六边形．一般一个足球上共有黑白皮块共32块，请你计算一下，黑色皮块有块．

查看试题解析
16. 幻方是古老的数学问题，我国古代的《洛书》中记载了最早的幻方——九宫格．将9个数填入幻方的空格中，要求每一横行、每一竖列以及两条对角线上的3个数之和相等．如图所示是一个未完成的幻方，则 $x - y =$ ．

查看试题解析

三、解答题（共12题，共68分）

17. 解方程组： ${\begin{array}{l} x = 2 y \\ x + y = 6 \end{array}$

查看试题解析
18. 解二元一次方程组： ${\begin{array}{l} 4 (x - y) = 8 - 3 y \\ \frac{x}{2} + \frac{y}{3} = 1 \end{array}$

查看试题解析
19. 列二元一次方程组求解应用题．
某商店用2200元购进《青春之歌》和《林海雪原》两种红色文化教育读本共100本，这两种的书籍的进价、标价如表所示：
书名
价格
青春之歌
林海雪原
进价（元∕本）
20
25
标价（元∕本）
30
40
（1）《青春之歌》、《林海雪原》各购进了多少本？
（2）若《青春之歌》按标价的9折出售，《林海雪原》按标价的8折出售，那么这两种书全部售出后，该商店共获利多少元？

查看试题解析
20. 下面是马小虎同学解二元一次方程组的过程，请认真阅读并完成相应的任务．
解方程组： $\{\begin{array}{l} 3 x - y = 4 ① \\ 6 x - 3 y = 10 ② \end{array}$
解：① $\times 2$ ，得 $6 x - 2 y = 8$ ． ③…（第一步）
② $-$ ③，得 $- 5 y = 2$ ，解得 $y = - \frac{2}{5}$ ， …（第二步）
将 $y = - \frac{2}{5}$ 代入①，得 $x = \frac{18}{15}$ …（第三步）
所以原方程组的解为 $\{\begin{matrix} x = \frac{18}{15} \\ y = - \frac{2}{5} \end{matrix}$ …（第四步）

(1)、这种求解二元一次方程组的方法叫做______法，以上求解步骤中，马小虎同学从第______步开始出现错误．

(2)、请写出此题正确的解答过程．

查看试题解析
21. 已知 $\{\begin{array}{l} m = 2 \\ n = 3 \end{array}$ 是关于 $m$ ， $n$ 的二元一次方程 $3 m + a n = 18$ 的一组解．

(1)、求 $a$ 的值；

(2)、请用含有 $m$ 的代数式表示 $n$ ．

查看试题解析
22. 在长方形 $A B C D$ 中，放入5个形状大小相同的小长方形（空白部分），其中 $A B = 8 cm$ ， $B C = 12 cm$ ，求图中阴影部分图形的面积．

查看试题解析
23. 某商场用6600元购进甲、乙两种节能灯共100只.甲种进价60元/只，售价80元/只；乙种进价70元/只，售价100元/只.

(1)、甲、乙两种节能灯各进了多少只?

(2)、全部售完这100只节能灯后，该商场获利多少元?

查看试题解析
24. 某校计划购买一批篮球和足球，已知购买 $2$ 个篮球和 $1$ 个足球共需 $320$ 元，购买 $3$ 个篮球和 $2$ 个足球共需 $540$ 元．求每个篮球和每个足球的售价？

查看试题解析
25. 某服装店用6200元购进A，B两种新式服装，按标价售出后可获得毛利润3300元．这两种服装的进价、标价见下表．
单价（元/件）
A种
B种
进价
200
320
标价
300
500

(1)、这两种服装各购进多少件？

(2)、如果A种服装按标价的8折售出、B种服装按标价的7.5折售出，那么这批服装全售完后，服装店比按标价售出收入减少多少元？

查看试题解析
26. 已知关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} 3 x + y = 10 m + 5 \\ x - 3 y = - 5 \end{array}$ ．

(1)、求方程组的解(用含 $m$ 的代数式表示)；

(2)、若方程组的解满足条件 $x < 1$ ，且 $y > 0$ ．求 $m$ 的取值范围．

查看试题解析
27. 为了增强学生体质，某校新增了羽毛球、乒乓球两大社团，现要购买一批羽毛球拍和乒乓球拍。已知购买2个羽毛球拍和3个乒乓球拍共需195元；购买3个羽毛球拍和2个乒乓球拍共需230元。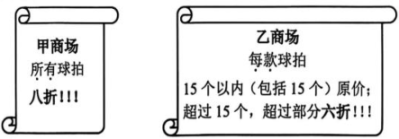

(1)、求羽毛球拍和乒乓球拍的销售单价。

(2)、甲、乙两个商场同时出售这两款球拍，现搞促销活动，海报信息如下：
设学校计划购买a个羽毛球拍，b个乒乓球拍，且两种球拍数量都大于15个，
①请分别计算参加每个商场促销活动的付款金额（用含a，b的代数式表示）.
②若付款金额相等，求a，b满足的数量关系.

查看试题解析
28. 《哪吒2魔童闹海》票房大卖，周边玩偶热销．某商家购进甲、乙两款玩偶进行销售，两次进货信息记录如下（两次进货单价分别相同）：

甲款数量/件
乙款数量/件
进货总费用/元
第一次
10
8
1020
第二次
6
12
900

(1)、求甲、乙两款玩偶的进货单价；

(2)、由于销售火爆，该商家决定第三次购进甲、乙两款玩偶共100件，若每件甲款玩偶的售价为110元，每件乙款玩偶的售价为70元，且销售完这100件玩偶所获得的利润不低于3700元，则商家最少需购进甲款玩偶多少件？

查看试题解析

	甲款数量/件	乙款数量/件	进货总费用/元
第一次	10	8	1020
第二次	6	12	900

单价（元/件）	A种	B种
进价	200	320
标价	300	500

北京版七（下）数学第五章 二元一次方程组 单元测试基础卷

一、选择题（每题2分，共16分）

二、填空题（每题2分，共16分）

三、解答题（共12题，共68分）

北京版七（下）数学第五章二元一次方程组单元测试基础卷